Operations Planning (Cambridge (CIE) A Level Business): Revision Note
Exam code: 9609
The need for operations planning
Operations planning is the process of organising all the resources and activities needed to produce goods or services efficiently
It ensures that the right products are made, at the right time, in the right quantity and using the right resources
Benefits of operations planning
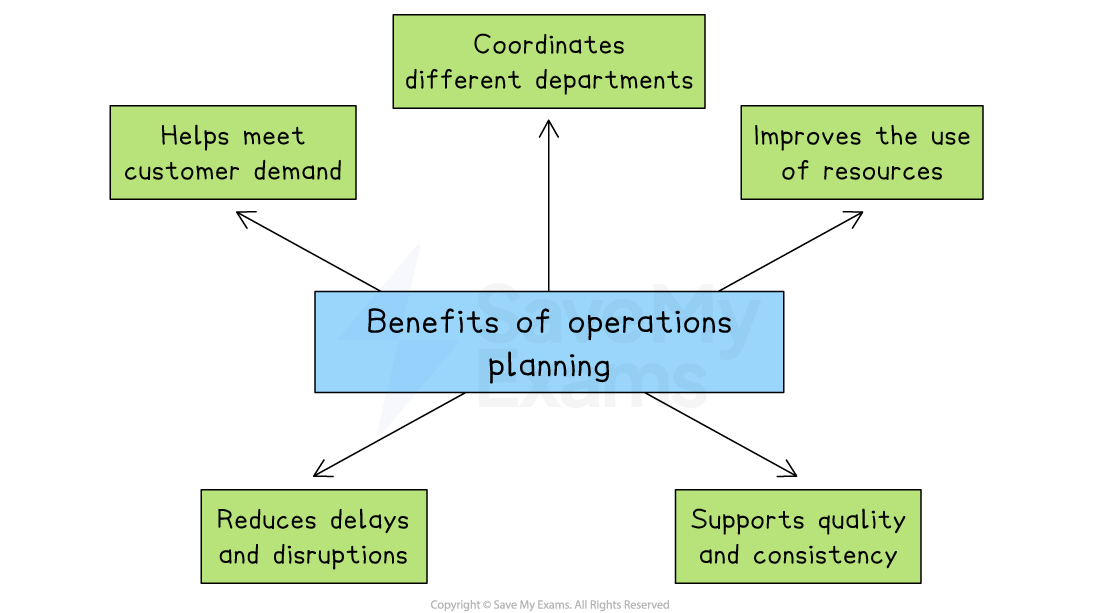
Meet customer demand
Planning helps businesses produce the correct quantity of goods to match expected demand
Without it, a business might make too little, causing stock shortages and lost sales,or too much, leading to waste and higher costs
Improve the use of resources
Operations planning ensures that staff, machinery and materials are used efficiently
It helps avoid wasted time, overuse of equipment, or running out of stock during production
Coordination of departments
Good planning allows production, purchasing, finance, and marketing to work together
E.g. Marketing can give sales forecasts, finance can set budgets and production can schedule output to meet targets
Reduces delays and disruptions
Planning helps identify potential problems early, such as a shortage of raw materials or a machine breakdown
Solutions can be prepared in advance, reducing the risk of disruption
Supports quality and consistency
Operations planning includes setting clear standards for quality, timing and workflows
This ensures that products or services are delivered consistently to meet customer expectations
An introduction to network diagrams
A network diagram is a visual planning tool used in operations management to help organise and schedule tasks in a project
It shows the order in which activities must be completed and how long each one is expected to take
Example network analysis

A network diagram must always start and end on a single node
Lines must not cross and must only be assigned to activities
How network diagrams help operations planning
Network diagrams improve time management by helping managers identify the critical path, the shortest time needed to complete a project
They highlight task dependencies by showing which activities must be completed before others can begin, helping to avoid mistakes and delays
Network diagrams support efficient resource allocation by showing when people, machines, or materials will be needed, reducing idle time and bottlenecks
They improve decision-making by making it easier to adjust plans if there are unexpected delays or changes to deadlines
Elements of network diagrams
Node
A node is a circle that represents a point in time where an activity either starts or finishes
Each node is split into three sections
The left half of the circle shows the activity number
The top right section shows the earliest start time (EST)—the earliest point an activity can begin, based on the completion of the previous activity
The bottom right section shows the latest finish time (LFT)—the latest time by which the previous activity must be completed without delaying the project
Activities
An activity is a task or process within a project that takes time to complete
Activities are shown on a network diagram as a line linking two nodes
Above the line, you will usually find either a letter or a short description of the activity
Duration
The duration is the length of time required to complete an activity
This is shown below the activity line and is usually measured in time units such as hours or days
Dummy activities
A dummy activity is an activity that has a weight of zero
Dummies are not assigned names (letters)
Dummies are represented by dotted lines
Where a dummy activity is used
To ensure each activity has a unique pair of start and end nodes
E.g. In the activity network below, activity D has immediate predecessors B and C
B and C cannot both start at event (node) 1 and end at event (node) 2 (this would not be a unique pair)
a dummy activity is used so that B has start and end pair (1, 3) and C has a start and end pair (1, 2)

When there is a split of immediate predecessors
E.g. In the activity network below, activity D has immediate predecessors B and C
Activity E only has B as an immediate predecessor
A dummy activity is used to show that D depends on both B and C

Using network diagrams for critical path analysis
1. Calculating earliest start times (EST)
Working forward from Node 1, it is possible to calculate the Earliest Start Time for each activity by adding the duration of each task

The EST for each activity is placed in the top right of each node
Node 1 is the starting point of the project and where both Activity A and Activity B begin
Activity A and Activity B are independent processes
Activity A has a duration of 2 days and its earliest start time (EST) is 0 days
Activity B has a duration of 3 days and its EST is also 0 days
Activity C and Activity D both begin at Node 2 and are dependent upon the completion of Activity A but are independent from each other
Activity C has a duration of 3 days and its EST is 2 days
Activity D has a duration of 5 days and its EST is also 2 days
Activity E begins at Node 3
Activity E has a duration of 4 days and its EST is 3 days
Activity F begins at Node 4
Activity F has a duration of 2 days and its EST is 5 days
Activity G begins at Node 5
Activity G has a duration of 1 day and its EST is 7 days
Activity H begins at Node 6
Activity H has a duration of 3 days and its EST is 7 days
Node 7 is the end point of the project
2. Calculating latest finish times (LFT)
Working backwards from Node 7, it is now possible to calculate the Latest Finish Time (LFT) for each activity by subtracting the duration of each task
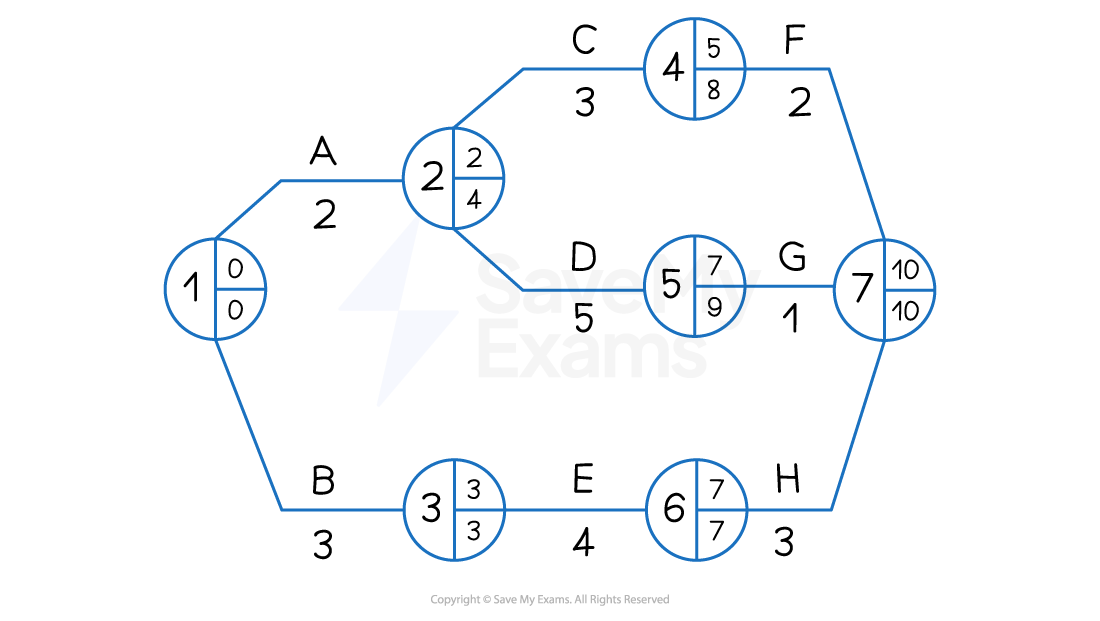
The LFT for each activity is placed in the bottom right of each node
Node 7 is the end point of the project, which has a latest finish time of 10 days
Activity H has a duration of 3 days
The LFT in Node 6 is 7 days (10 days - 3 days)
Activity G has a duration of 1 day
The LFT in Node 5 is 9 days (10 days - 1 day)
Activity F has a duration of 2 days
The LFT in Node 4 is 8 days (10 days - 2 days)
Activity E has a duration of 4 days
The LFT in Node 3 is 3 days (7 days - 4 days)
Activity D has a duration of 5 days
The LFT in Node 2 is 4 days (9 days - 5 days)
Activity C has a duration of 3 days
The LFT in Node 3 is 4 days because Activity D is the more time-critical of the two activities that are dependent upon the completion of Activity A and so its LFT is recorded
Activity B has a duration of 3 days
The LFT in Node 1 is 0 days (3 days - 3 days)
Activity A has a duration of 2 days
The LFT in Node 1 is 0 days because Activity B is the more time-critical of the two starting activities and so its LFT is recorded
The LFT in Node 1 is always 0
3. Identifying the critical path
The critical path highlights those activities that determine the length of the whole project
If any of these critical activities are delayed, the project as a whole will be delayed
The critical path follows the nodes where the EST and LFT are equal
In the diagram below nodes 1 3 6 and 7 have equal ESTs and LFTs
Activities that determine these nodes are B E and H
These activities are marked with two short lines
The critical path is therefore BEH
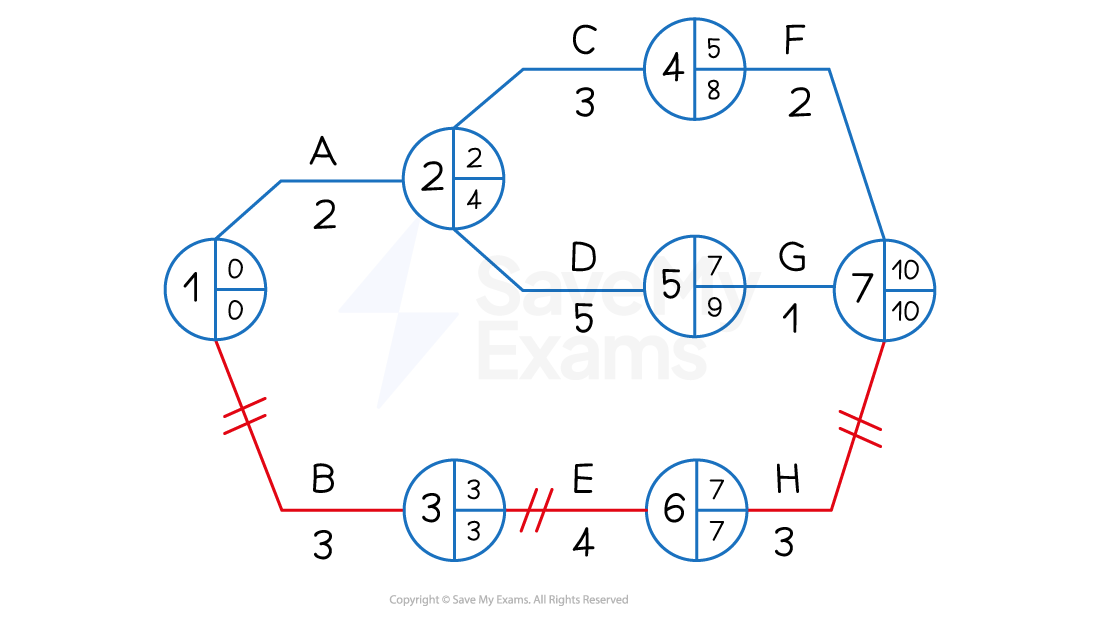
4. Identifying and calculating float time
Float time exists where there is a difference between the Earliest Start Time (EST and the Latest Finish Time (LFT)
Where float time is identified, managers may
Transfer resources such as staff or machinery to more critical activities
Allow extra time to complete tasks to improve quality or allow for creativity

Float time analysis
The total float refers specifically to spare time that is available so that the overall project completion is not delayed
The total float for a specific activity is calculated by
Using the diagram above, the following total float times can be calculated for Activities A to H:
Activity | LFT | - Duration | - EST | = Total Float |
|---|---|---|---|---|
A | 4 | 2 | 0 | 2 |
B | 3 | 3 | 0 | 0 |
C | 8 | 3 | 2 | 3 |
D | 9 | 5 | 2 | 2 |
E | 7 | 4 | 3 | 0 |
F | 10 | 2 | 5 | 3 |
G | 10 | 1 | 7 | 2 |
H | 10 | 3 | 7 | 0 |
The critical activities B E and H each have a total float of 0 days
Worked Example
The network diagram below shows the activities involved in a new promotional campaign for a small fashion accessories business as well as the time (in weeks) it is expected that each activity will take to complete.
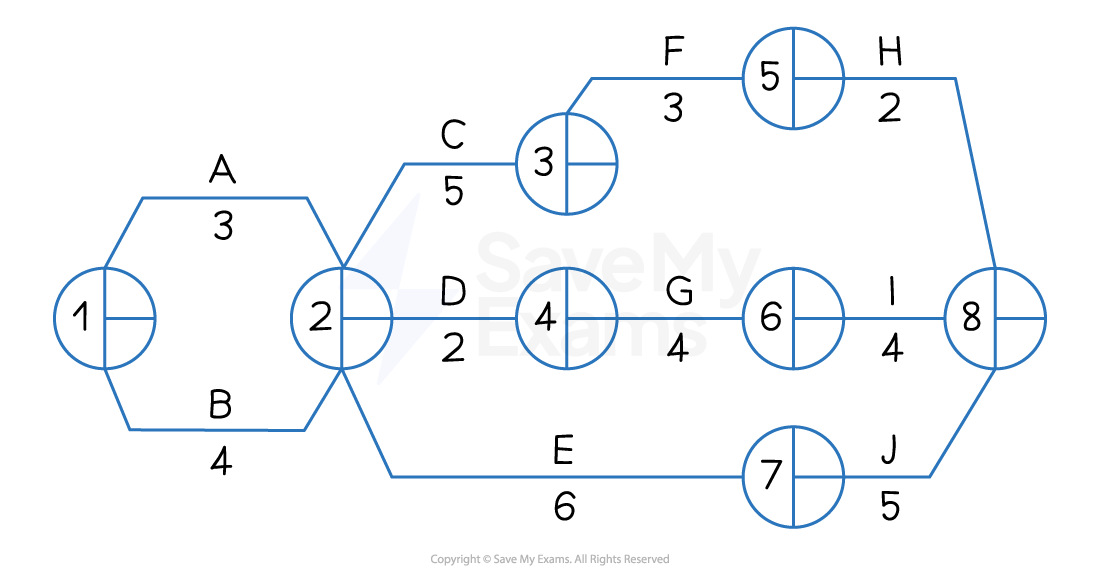
Calculate
a) The earliest start times and latest finish times for each node.
[4]
b) The total float time for activity G
[2]
Step 1: Calculate the Earliest Start Times (EST)
Node 1 EST = 0
Node 2 EST = 0 + 3 = 3 but 0 + 4 = 4 so 4
Node 3 EST = 4 + 5 = 9
Node 4 EST = 4 + 2 = 6
Node 5 EST = 9 + 3 = 12
Node 6 EST = 6 + 4 = 10
Node 7 EST = 4 + 6 = 10
Node 8 EST = 12 + 2 = 14 but 10 + 4 = 14 and 10 + 5 = 15 so 15 (2)
Step 2: Calculate the Latest Finish Times (LFT)
Node 8 = 15
Node 7 = 15 - 5 = 10
Node 6 = 15 - 4 = 11
Node 5 =15 - 2 = 13
Node 4 =11 - 4 = 7
Node 3 =13 - 3 = 10
Node 2 = 10 - 6 = 4
Node 1 = 4 - 4 = 0 (2)
Step 3: Calculate the total float time for Activity G
(2)
Amending network diagrams
If the length of time taken to complete an activity changes, there may be an effect on the critical path and available float

In the strategy shown in the network diagram above, the duration of activity G is increased from 1 to 4 days
The EST at node 7 will increase to 11 days and the LFT to 11 days
The EST at node 5 will remains at 11 days, while the LFT will change to 7 days
The EST at node 5 will remains at 2 days, while the LFT will change to 2 days
As a result, the critical path will switch from BEH to ADG

Evaluating critical path analysis
Although critical path analysis can be useful in project planning, the method has some limitations
Limitations of critical path analysis
Limitations | Explanation |
|---|---|
|
|

Unlock more, it's free!
Was this revision note helpful?