Momentum & Impulse with Vectors (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Impulse-momentum principle with vectors
How do impulse and momentum work in 2D?
Impulse and momentum can be used in 2D as they are vector quantities
Impulse in 2D essentially works the same way as impulse in 1D
For a constant force given by the vector
N acting on a particle for
seconds the impulse is given by the vector:
The units are still N s (equivalent to kg m s-1 )
For a particle of mass
the impulse is still equal to the change in momentum
or
where u m s-1 is the initial velocity vector and v m s-1 is the final velocity vector
are all vector quantities, and
is a scalar
If using column vectors, this equation would look as follows:
How are questions different in 2D?
You could be asked to work out the magnitude of the impulse
You would need to find the two components of the impulse vector and then use Pythagoras
You could be asked to work out the direction of the impulse
You would need to find the two components of the impulse vector and then use SOHCAHTOA (right-angled trigonometry)
You might need to find the angle between the impulse and the vector
or
so always draw a sketch
If you know the magnitude and direction of the impulse or a velocity, then you might have to resolve it into horizontal and vertical components
Examiner Tips and Tricks
Be careful with negatives, especially when adding and subtracting vectors
When finding angles and directions always sketch a diagram. Read the question carefully to help you decide where the angle should be measured from
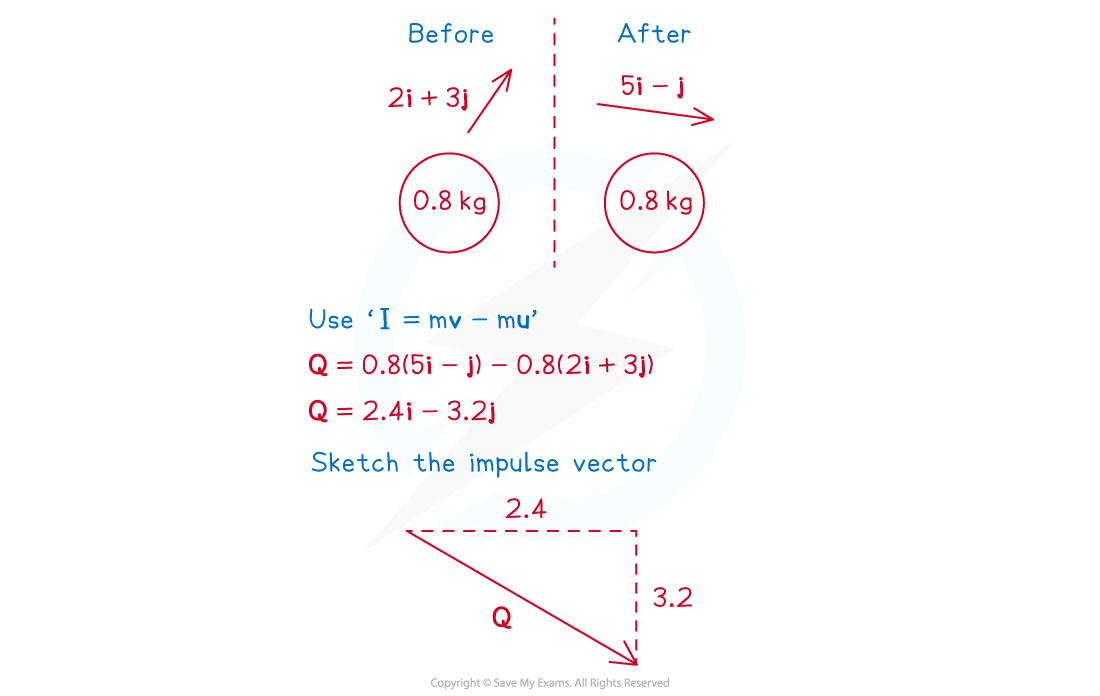
Worked Example
A ball of mass 0.8 kg is moving with velocity when it receives an impulse Q N s . Immediately after receiving the impulse, the velocity of the ball is
.
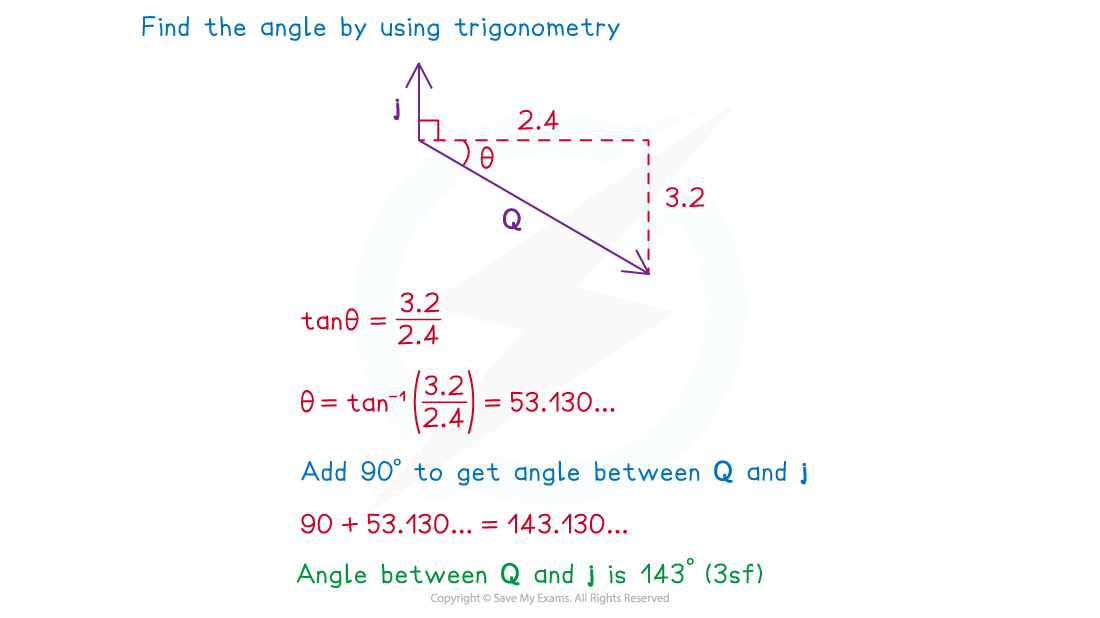
Find the magnitude of the impulse Q N, and its angle from the vector j.


Unlock more, it's free!
Did this page help you?