Moments (Edexcel A Level Maths: Mechanics): Exam Questions

 is a light rod, and  is the point on such that .  A force of 14 N is applied to the rod at point , with the line of action of the force making an angle of  with  as shown in the diagram below:

Given that the moment of the force about point  is 2.24 Nm  clockwise, find

(i) the length of rod ,

(ii) the moment of the force about point .

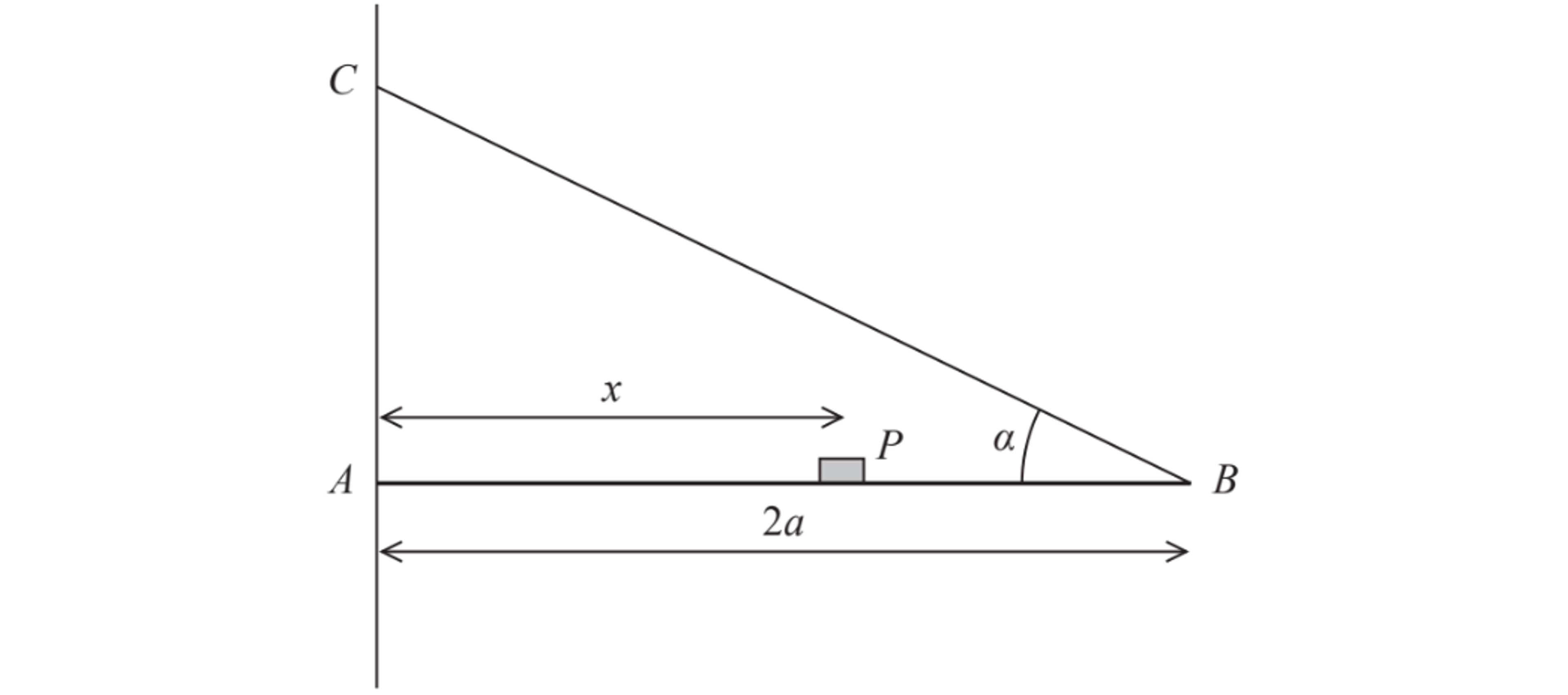
 is a triangular lamina in which angle  is a right angle, and the lengths of sides  and  are 58 cm and 42 cm respectively. 

Three forces are applied to the lamina at points  as shown in the diagram below.

Calculate the resultant moment about point .

 is a uniform rod of mass 6 kg and length 2 m, with a load of mass  kg attached at point . 

is held horizontally in equilibrium by two vertical wires attached at points  and , such that  as shown in Figure 1.

The tension in the wire at  is found to be eight times the tension in the wire at .  By modelling the load at  as a particle, find the value of .

Figure 1 shows a ladder  of length 10 m and mass 34 kg. 

End  of the ladder rests on a smooth vertical wall, while end rests on rough horizontal ground. 

The ladder rests in limiting equilibrium at an angle of  with the ground.

The ladder is modelled as a uniform rod lying in a vertical plane perpendicular to the wall. 

The coefficient of friction between the ground and the ladder is .

Find the value of to 3 significant figures.

Figure 1 shows a uniform plank of length 8 m. It rests horizontally on two supports, one of which is placed at point and the other of which is placed 2.4 m from point . The plank can be modelled as a rod.

A person with a weight of 728 N stands on the plank at point and begins to walk towards point .

When they have walked a distance of 0.6 m, the plank is on the point of tilting.

Calculate the weight of the plank.

The person would like to be able to stand at point without the plank tilting.

Given that the rock may be modelled as a particle, find the minimum weight of the rock required.

Figure 1 shows a non-uniform rod of mass 10 kg and length 3 m.

A load of mass 26 kg is attached at point .

The rod is held horizontally in equilibrium by two vertical wires attached at points and , such that .

 The position of the centre of mass of the rod is indicated by point .  The load at may be modelled as a particle.

Given that the rod is on the point of tilting about , determine the location of the centre of mass of the rod.

Give your answer as the value of ; the distance of the centre of mass from point .

The load is then removed from point , and the rod is left suspended in horizontal equilibrium from the two wires.

Determine the tensions in the wires at  and at after the load is removed.

Give your answer in terms of the gravitational constant of acceleration .

Figure 1 shows a ladder of length 5 m and mass 17 kg. 

End of the ladder is resting against a smooth vertical wall, while end rests on rough horizontal ground so that the ladder makes an angle of  70° with the ground.

The ladder is modelled as a uniform rod lying in a vertical plane perpendicular to the wall. The coefficient of friction between the ground and the ladder is .

Given that the ladder is at rest in limiting equilibrium, calculate the value of to 3 significant figures.

Figure 1 shows a uniform rod of length 2 m and weight 60 N. 

End of the rod is in contact with rough horizontal ground.  The rod also rests against a smooth cylindrical peg that makes contact with the rod at point such that . The rod remains in equilibrium, making an angle of 30° with the ground.

 The magnitude of the normal reaction force exerted by the peg on the rod at point C is denoted by .

Show that .

The magnitude of the normal reaction force exerted by the ground on the rod at point  is denoted by , and the magnitude of the frictional force between the ground and the rod at point  is denoted by .

Find the exact values of  and .

The coefficient of friction between the ground and the rod is denoted by .

Given that the rod is on the point of slipping, find the exact, simplified value of .

A ladder has mass and length .

The end of the ladder is on rough horizontal ground.

The ladder rests against a fixed smooth horizontal rail at the point .

The point is at a vertical height above the ground.

The vertical plane containing is perpendicular to the rail.

The ladder is inclined to the horizontal at an angle , where , as shown in Figure 1.

The coefficient of friction between the ladder and the ground is .

The ladder rests in limiting equilibrium.

The ladder is modelled as a uniform rod.

Using the model, show that the magnitude of the force exerted on the ladder by the rail at is .

Hence, or otherwise, find the value of .

A uniform rod has mass and length .

A particle of mass is attached to the rod at the point , where .

The rod rests with its end on rough horizontal ground.

The rod is held in equilibrium at an angle to the ground by a light string that is attached to the end of the rod.

The string is perpendicular to the rod, as shown in Figure 2.

Explain why the frictional force acting on the rod at A acts horizontally to the right on the diagram.

The tension in the string is .

Show that .

Given that , show that the magnitude of the vertical force exerted by the ground on the rod at is .

The coefficient of friction between the rod and the ground is .

Given that the rod is in limiting equilibrium, show that .

is a non-uniform rod of mass 10 kg and length 3 m. 

rests horizontally on two supports placed at points and , where  as shown in Figure 1.

Esme attaches a 9 kg mass to the rod at a point between and which is 0.4 m from , and measures the reaction force at . 

She then removes the mass and reattaches it to the rod at a point between and , which is 0.4 m from , and again measures the reaction force at . 

She finds that in her second measurement the reaction force at  is one third of the size of the reaction force at  in her first measurement.

By modelling the attached mass as a particle, use the above information to determine the position of the centre of mass of rod .

State your answer as the distance of the centre of mass from point .

Figure 1 shows a uniform beam  of length 4 m.  It rests horizontally on two supports placed at points  and , such that  and .

A stone of mass 10 kg is placed at point  and the beam is on the point of tilting. 

That stone is removed, and another stone of mass  kg is placed at point  which causes the beam to begin tilting.

Given that the stones may be modelled as particles, show that ,  where  is the largest possible constant for which this inequality must be true.

is a non-uniform rod of mass 12 kg and length 4 m.  is held horizontally in equilibrium by a support placed at point  and a vertical wire attached to point such that  and  as shown in Figure 1.

An object of mass 15 kg is attached to the rod at point  which causes the rod to be on the point of tilting about . 

The object is then removed.

Find the ratio of the reaction force at  to the tension in the wire at when there are no objects attached to the rod. 

Give your answer in the form  where  and  are integers with no common factors other than 1.

The 15 kg object is then attached to the rod between points  and .

Find the greatest distance to the left of point  that the object can be attached without the rod beginning to tilt.

Figure 1 shows a ladder  of length 10 m and mass 34 kg.  End  of the ladder is resting against a smooth vertical wall, while end  rests on rough horizontal ground so that the ladder makes an angle of  with the ground.

A house-painter who has a mass of 75 kg has decided to climb up the ladder without taking any additional precautions to prevent the bottom of the ladder from slipping. 

The ladder may be modelled as a uniform rod lying in a vertical plane perpendicular to the wall, and the house-painter may be modelled as a particle. 

The coefficient of friction between the ground and the ladder is 0.4.

Determine the vertical height above the horizontal ground the house-painter is able to reach before the ladder slips.

Figure 1 shows a uniform rod of length 2.4 m and weight 72 N. 

End  of the rod is in contact with rough horizontal ground. 

The rod rests against a smooth cylindrical peg that makes contact with the rod at point  such that  and . 

The rod remains stationary and in equilibrium, making an angle of  with the ground as shown in Figure 1.

The coefficient of friction between the ground and the rod is . 

Given that the rod is on the point of slipping, calculate the value of .

Figure 1 shows a uniform rod of mass 4 kg and length 1.2 m.

 is held horizontally in equilibrium by two vertical wires attached 0.8 m apart at points and , where is 0.3 m from .

A particle of mass kg is attached to at the point , such that remains in horizontal equilibrium and the tensions in the wires at and are equal.

Given that point is in between points and , show that .

A beam has mass and length .

The beam rests in equilibrium with on rough horizontal ground and with against a smooth vertical wall.

The beam is inclined to the horizontal at an angle , as shown in Figure 2.

The coefficient of friction between the beam and the ground is .

The beam is modelled as a uniform rod resting in a vertical plane that is perpendicular to the wall.

Using the model, show that .

A horizontal force of magnitude , where is a constant, is now applied to the beam at .

This force acts in a direction that is perpendicular to the wall and towards the wall.

Given that , and the beam is now in limiting equilibrium, use the model to find the value of .

A ramp, , of length 8 m and mass 20 kg, rests in equilibrium with the end on rough horizontal ground.

The ramp rests on a smooth solid cylindrical drum which is partly under the ground. The drum is fixed with its axis at the same horizontal level as .

The point of contact between the ramp and the drum is , where = 5 m, as shown in Figure 2.

The ramp is resting in a vertical plane which is perpendicular to the axis of the drum, at an angle to the horizontal, where .

The ramp is modelled as a uniform rod.

Explain why the reaction from the drum on the ramp at point acts in a direction which is perpendicular to the ramp.

Find the magnitude of the resultant force acting on the ramp at .

The ramp is still in equilibrium in the position shown in Figure 2 but the ramp is now not modelled as being uniform.

Given that the centre of mass of the ramp is assumed to be closer to than to , state how this would affect the magnitude of the normal reaction between the ramp and the drum at .

A rod has mass and length .

The rod has its end on rough horizontal ground and its end against a smooth vertical wall.

The rod makes an angle with the ground, as shown in Figure 3.

The rod is at rest in limiting equilibrium.

State the direction (left or right on Figure 3 above) of the frictional force acting on the rod at . Give a reason for your answer.

The magnitude of the normal reaction of the wall on the rod at is .

In an initial model, the rod is modelled as being uniform.

Use this initial model to answer parts (b), (c) and (d).

By taking moments about , show that

The coefficient of friction between the rod and the ground is .

Given that , find the value of .

Find, in terms of and , the magnitude of the resultant force acting on the rod at .

In a new model, the rod is modelled as being non-uniform, with its centre of mass closer to than it is to .

A new value for is calculated using this new model, with .

State whether this new value for is larger, smaller or equal to the value that would take using the initial model. Give a reason for your answer.

A plank, , of mass and length , rests with its end against a rough vertical wall.

The plank is held in a horizontal position by a rope. One end of the rope is attached to the plank at and the other end is attached to the wall at the point , which is vertically above .

A small block of mass is placed on the plank at the point , where .

The plank is in equilibrium in a vertical plane which is perpendicular to the wall.

The angle between the rope and the plank is , where , as shown in Figure 3.

The plank is modelled as a uniform rod, the block is modelled as a particle and the rope is modelled as a light inextensible string.

Using the model, show that the tension in the rope is .

The magnitude of the horizontal component of the force exerted on the plank at by the wall is .

Find in terms of .

The force exerted on the plank at by the wall acts in a direction which makes an angle with the horizontal.

Find the value of .

The rope will break if the tension in it exceeds .

Explain how this will restrict the possible positions of . You must justify your answer carefully.

ABC is a triangular lamina in which the size of angle ACB is indicated by θ. D is the point on BC such that .  A 165 N force acts on point B in a direction perpendicular to AC and a 420 N force acts on point D in a direction parallel to AC, as shown in the diagram below:

Given that the resultant force about point C is in the clockwise direction, show that .

Figure 1 shows a non-uniform rod of length and mass . 

A particle of mass is attached to the rod at point , and the rod is then set to rest horizontally on two supports at points and , where   and .

Given that the rod is at the point of tilting, find the two possible locations of the centre of mass of the rod.

In your answers give the distance of the centre of mass from point , with the values given in terms of .

Figure 1 shows a uniform rod of length and mass . 

End of the rod is in contact with rough horizontal ground. 

The rod rests against a smooth cylindrical peg that contacts the rod at point such that the distance from point to point is , where  

The vertical plane containing the rod is perpendicular to the peg. The rod remains stationary in this configuration, making an angle of  with the ground.

The coefficient of friction between the ground and the rod is . 

It may be assumed that

Show that

Figure 1 shows a ladder of length and mass . 

End of the ladder is resting against a rough vertical wall, while end rests on rough horizontal ground so that the ladder makes an angle of with the ground.

 A person with mass is standing on the ladder a distance from end .

The ladder may be modelled as a uniform rod lying in a vertical plane which is perpendicular to the wall, and the person may be modelled as a particle.

The coefficient of friction between the wall and the ladder is , and the coefficient of friction between the ground and the ladder is .

It may be assumed that .

Given that the ladder is at rest in limiting equilibrium, show that

where is the normal reaction force exerted by the ground on the ladder at point  and where  is the constant of acceleration due to gravity.