Area between 2 curves (OCR A Level Maths: Pure)

What is the area between two curves?

• Ensure you are familiar with …
  • Area under a curve
  • Area between a line and a curve

  

• In general find the definite integral of “upper curve” – “lower curve”
• However this does depend on …
  • … the area being found
  • … if the curves intersect (and cross over)

• The area may have to be split into separate integrals

  

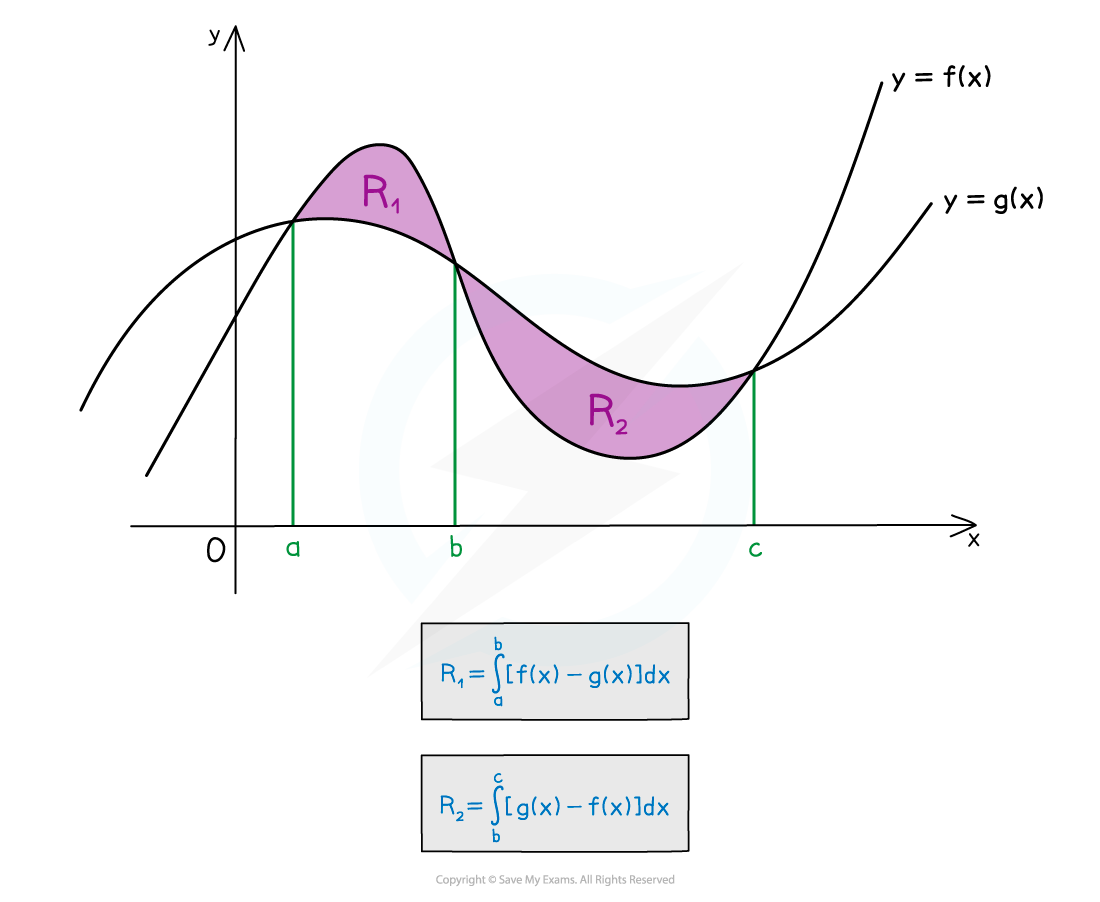
• The points at which curves intersect may need to be calculated

How do I find the area between two curves?

•  STEP 1: Find the intersections of the curves if needed
• STEP 2: Form the integral …
  • … using the intersections as limits
  • … “upper curve” – “lower curve” …
  • … and find the value of the integral
• STEP 3: Repeat STEP 2 if more than one area needed
• STEP 4: Add areas together