Approximating the Poisson Distribution (Edexcel International A Level Maths: Statistics 2)

Calculating probabilities using a binomial or Poisson distribution can take a while. Under certain conditions we can use a normal distribution to approximate these probabilities. As we are going from a discrete distribution (binomial or Poisson) to a continuous distribution (normal) we need to apply continuity corrections.

What are continuity corrections?

• The binomial and Poisson distribution are discrete and the normal distribution is continuous
• A continuity correction takes this into account when using a normal approximation
• The probability being found will need to be changed from a discrete variable, X to a continuous variable, X_N
  • For example, X = 4 for Poisson can be thought of as   for normal as every number within this interval rounds to 4
  • Remember that for a normal distribution the probability of a single value is zero so 

How do I apply continuity corrections?

• Think about what is largest/smallest integer that can be included in the inequality for the discrete distribution and then find its upper/lower bound
• 
• 
  
  • You add 0.5 as you want to include  in the inequality
• 
  • You subtract 0.5 as you don't want to include  in the inequality
• 
  • You subtract 0.5 as you want to include  in the inequality
• 
  • You add 0.5 as you don't want to include  in the inequality
• For a closed inequality such as 
  • Think about each inequality separately and use above
  • 
  • 
  • Combine to give
  • 

When can I use a normal distribution to approximate a Poisson distribution?

• A Poisson distribution   can be approximated by a normal distribution  provided
  • is large
• Remember that the mean and variance of a Poisson distribution are approximately equal, therefore the parameters of the approximating distribution will be:
  • 
  • 
  • 
• The greater the value of λ in a Poisson distribution, the more symmetrical the distribution becomes and the closer it resembles the bell-shaped curve of a normal distribution

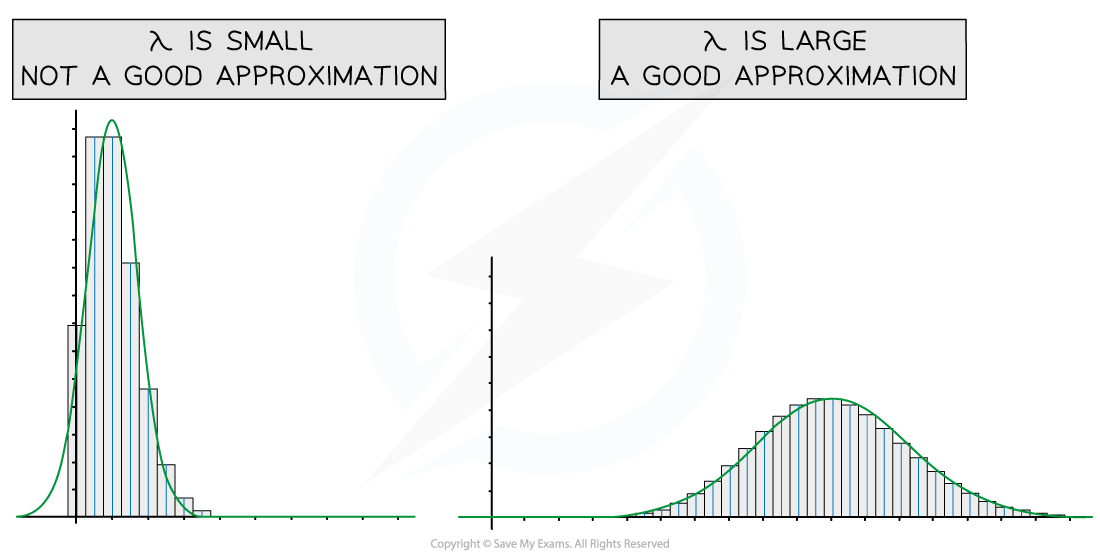
Why do we use approximations?

• If there are a large number of values for a Poisson distribution there could be a lot of calculations involved and it is inefficient to work with the Poisson distribution
  • These days calculators can find Poisson probabilities so approximations are no longer necessary
  • However it can still be easier to work with a normal distribution
    • You can calculate the probability of a range of values quickly
    • You can use the inverse normal distribution function (most calculators don't have an inverse Poisson distribution function)

How do I approximate a probability?

• STEP 1: Find the mean and variance of the approximating distribution
  • • 
• STEP 2: Apply continuity corrections to the inequality
• STEP 3: Find the probability of the new corrected inequality
  • • Find the standard normal probability and use the table of the normal distribution
• The probability will not be exact as it is an approximation but provided λ is large enough then it will be a close approximation