A* Algorithm (Cambridge (CIE) A Level Computer Science): Revision Note

A* algorithm

What is the A* algorithm?

• The A* (A-star) algorithm is a pathfinding algorithm that builds upon Dijkstra’s algorithm

• It introduces a heuristic function to improve efficiency

• It is used to find the shortest path from a starting node to a goal node in a graph

• While Dijkstra’s algorithm considers only the actual cost from the start node:

  • A* enhances this by estimating the remaining distance to the goal

  • This makes it more goal-oriented and often more efficient

How A* improves on Dijkstra’s

• To avoid inefficient detours, A* introduces a heuristic function, called h(x)

• It estimates the straight-line distance (Euclidean distance) from the current node to the goal

• A* combines both cost and estimate using the formula:

  • f(x) = g(x) + h(x)

    • g(x) = the actual cost from the start node to the current node

    • h(x) = the heuristic estimate to the goal node

    • f(x) = the total estimated cost of the cheapest solution through node x

• By choosing nodes with the lowest f(x) value, A* aims to explore paths that are both cheap and move closer to the goal

Heuristics in A*

• The heuristic function h(x) should never overestimate the true cost to the goal

• This ensures A* remains optimally efficient

• The closer h(x) is to the true cost, the fewer nodes A* needs to explore

• If h(x) increases, it may indicate the algorithm is moving away from the goal, helping it backtrack or choose a better path

• Below is an illustration of the A* search:

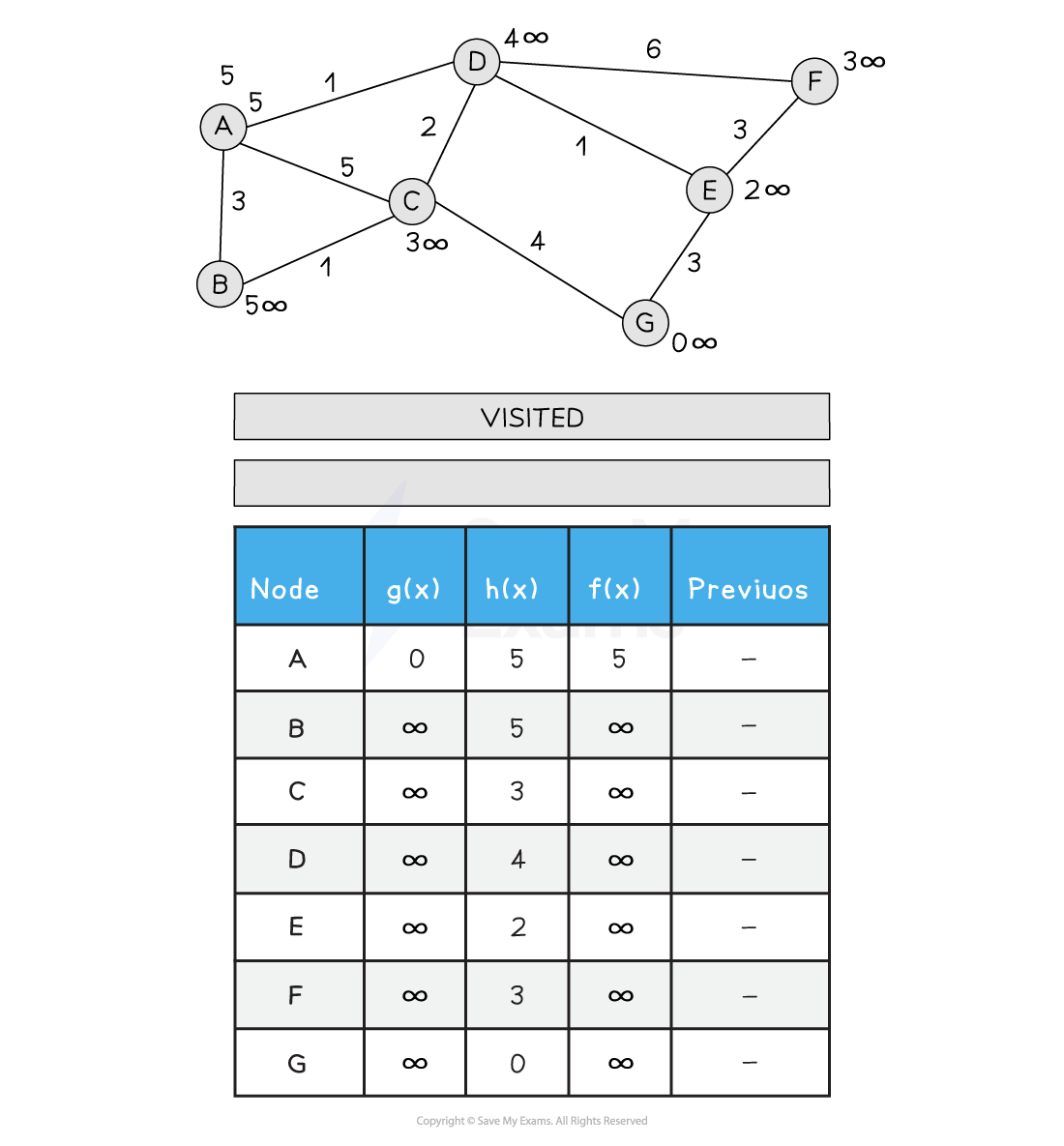
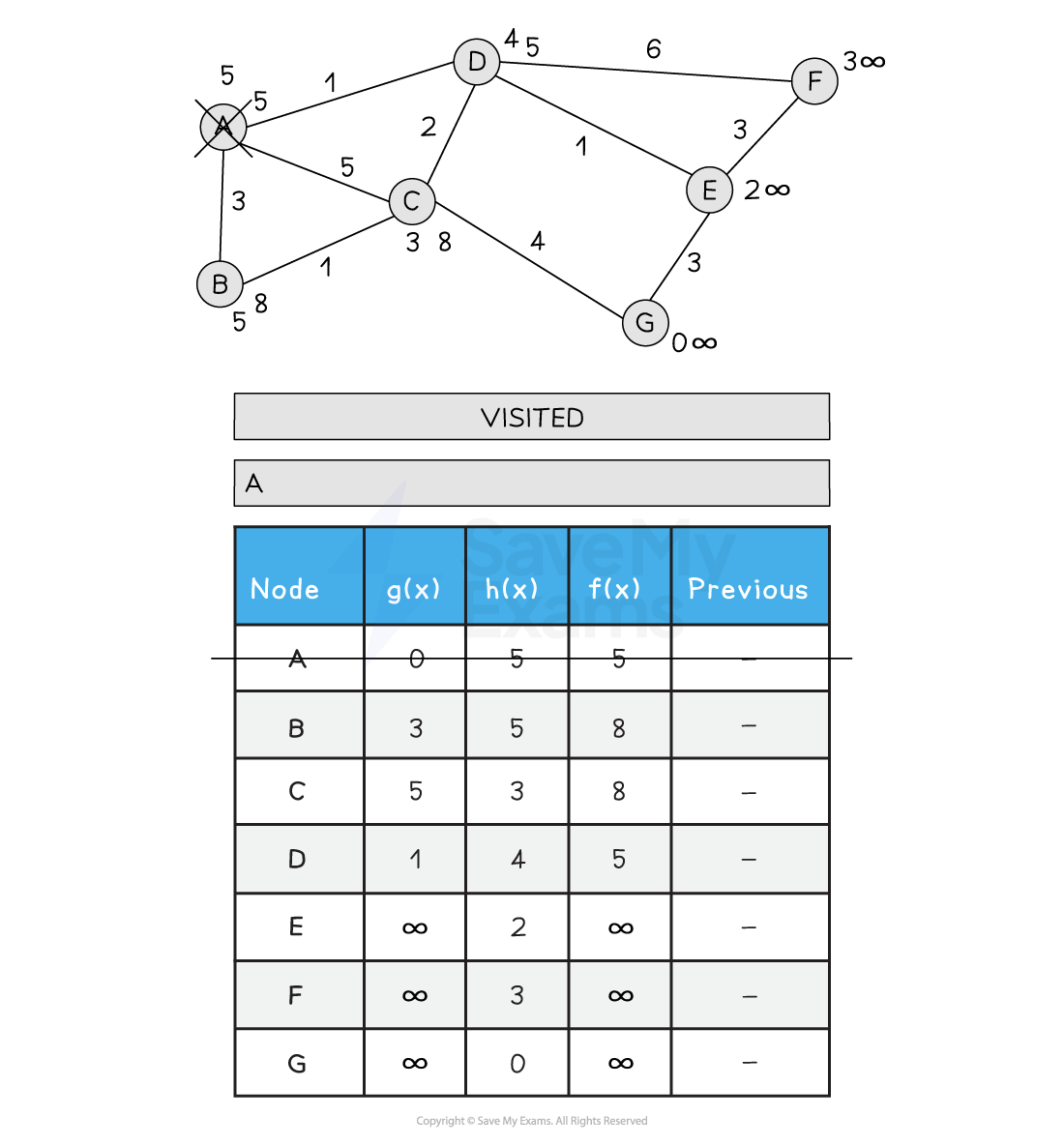
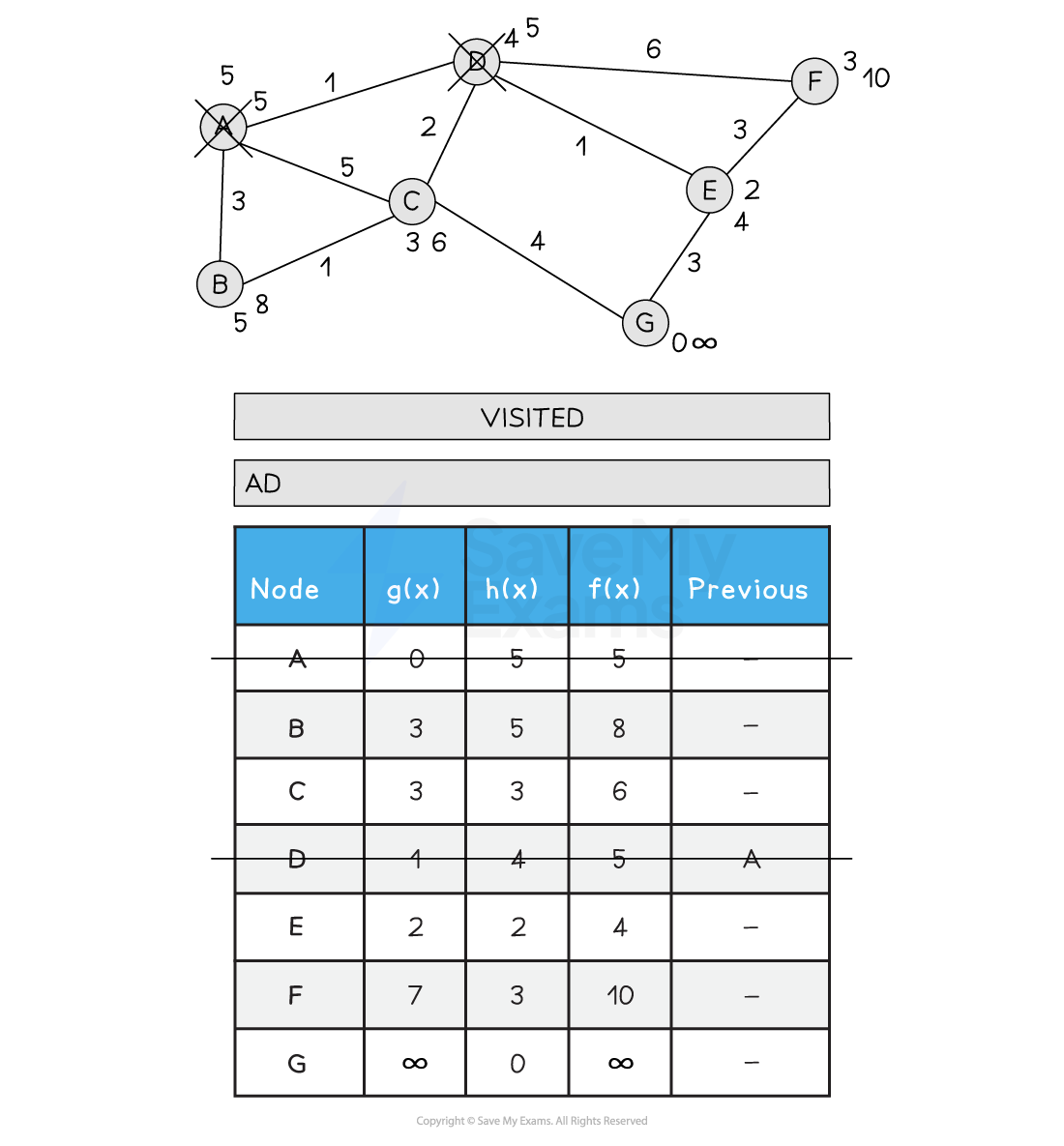
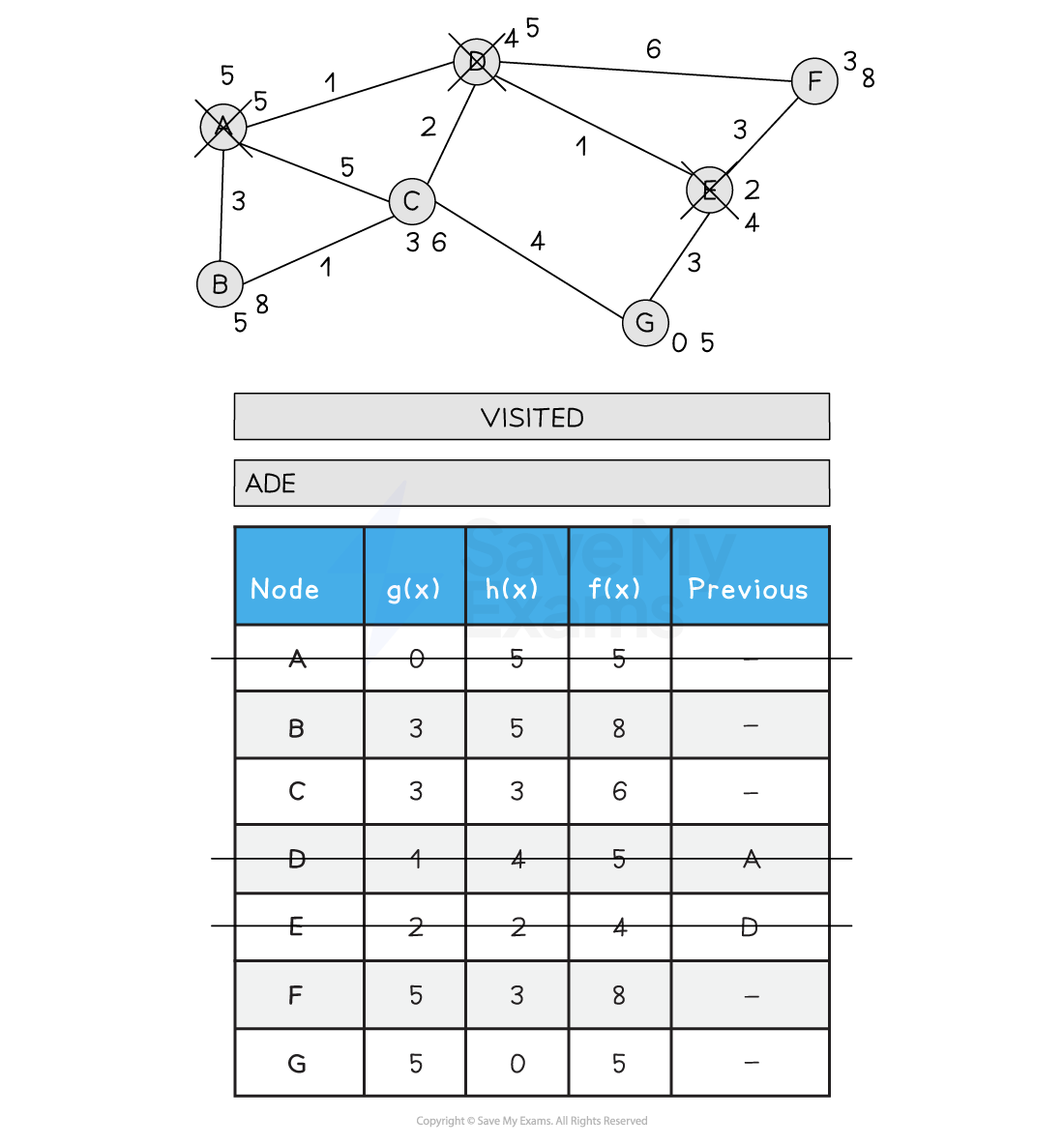
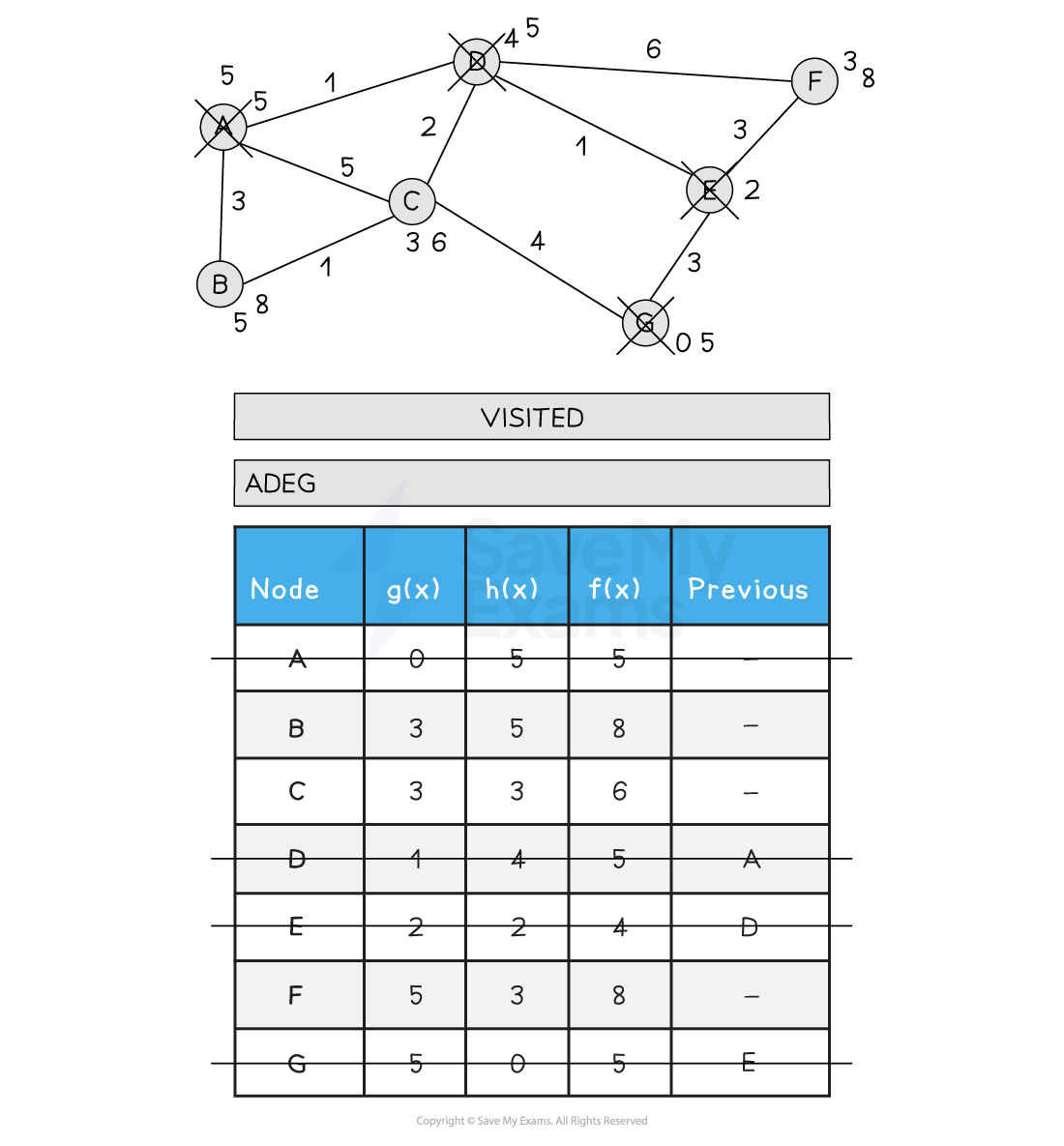
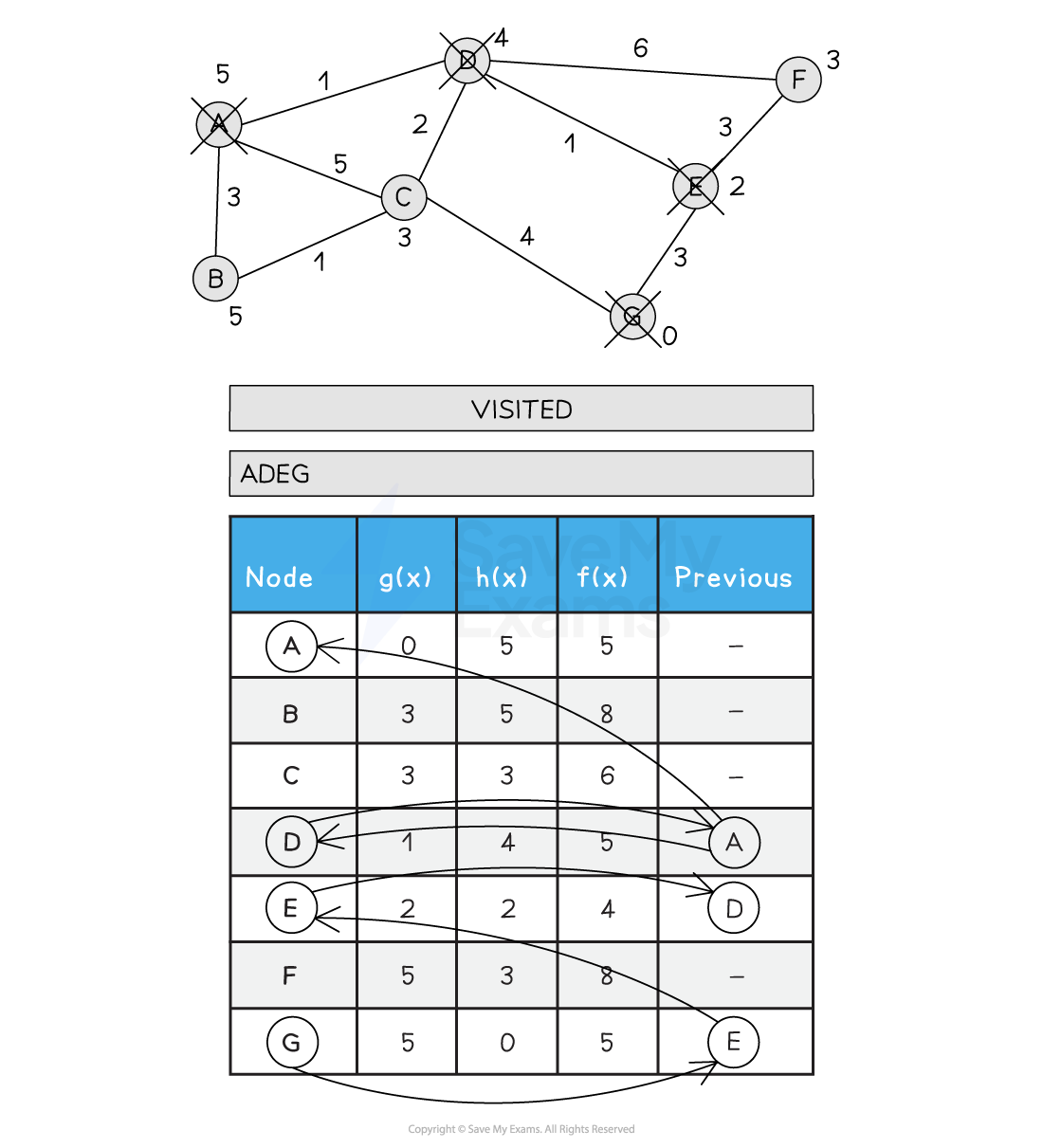
Figure 2: Performing the A* Search

A* vs Dijkstra’s

Programming A* algorithm

How do you write an A* algorithm?

Pseudocode

FUNCTION AStarSearch(graph, start, goal)

    // Initialise distances and f-scores
    FOR EACH node FROM graph
        SET g[node] TO infinity
        SET f[node] TO infinity
    NEXT node

    SET g[start] TO 0
    SET f[start] TO h[start]

    DECLARE openSet AS LIST
    ADD start TO openSet

    WHILE openSet IS NOT EMPTY

        // Find node in openSet with the lowest f value
        SET min TO null
        FOR EACH node FROM openSet
            IF min = null THEN
                SET min TO node
            ELSEIF f[node] < f[min] THEN
                SET min TO node
            ENDIF
        NEXT node

        IF min = goal THEN
            EXIT WHILE
        ENDIF

        REMOVE min FROM openSet

        // Check all neighbours of current node
        FOR EACH neighbour FROM graph[min]
            SET tentativeG TO g[min] + cost(min, neighbour)

            IF tentativeG < g[neighbour] THEN
                SET g[neighbour] TO tentativeG
                SET f[neighbour] TO g[neighbour] + h[neighbour]
                SET previousNode[neighbour] TO min

                IF neighbour NOT IN openSet THEN
                    ADD neighbour TO

• graph[min] assumes you're storing adjacency lists

• h[node] is your heuristic table

• g[] and f[] are maps (dictionaries) for real cost and estimated total cost

• cost(min, neighbour) should be defined or assumed available

Python

def a_star_search(graph, start, goal, h):
    open_set = [start]
    g = {node: float('inf') for node in graph}
    f = {node: float('inf') for node in graph}
    came_from = {}

    g[start] = 0
    f[start] = h[start]

    while open_set:
        # Get node with lowest f value
        current = min(open_set, key=lambda node: f[node])

        if current == goal:
            break

        open_set.remove(current)

        for neighbour, cost in graph[current]:
            tentative_g = g[current] + cost

            if tentative_g < g[neighbour]:
                g[neighbour] = tentative_g
                f[neighbour] = g[neighbour] + h[neighbour]
                came_from[neighbour] = current

                if neighbour not in open_set:
                    open_set.append(neighbour)

    # Reconstruct path
    path = []
    node = goal
    while node != start:
        path.append(node)
        node = came_from[node]
    path.append(start)
    path.reverse()

    return path

Example usage:

graph = {
    'A': [('B', 2), ('C', 5)],
    'B': [('D', 4)],
    'C': [('D', 1)],
    'D': [('E', 3)],
    'E': []
}

h = {
    'A': 7,
    'B': 6,
    'C': 4,
    'D': 2,
    'E': 0
}

print(a_star_search(graph, 'A', 'E', h))

Output:

• A possible shortest path from 'A' to 'E', guided by the heuristic values