Dijkstra's Shortest Path Algorithm (Cambridge (CIE) A Level Computer Science): Revision Note

Dijkstra’s shortest path algorithm

• In Computer Science, an optimisation problem involves finding the most efficient solution to a given problem

• This could mean minimising cost, time, or resource usage, or maximising output, efficiency, or value

• Examples of optimisation problems include:

  • Finding the shortest route between two locations (e.g. Google Maps)

  • Minimising resource usage in manufacturing or video games

  • Creating efficient timetables (e.g. for schools or offices)

  • Scheduling tasks and staff shifts to avoid conflicts or downtime

• One of the most common real-world examples is finding the shortest path from A to B, which is exactly what Dijkstra’s algorithm solves

What is Dijkstra’s shortest path algorithm?

• In A Level Computer Science, Dijkstra’s shortest path algorithm is a classic optimisation algorithm

• It calculates the shortest path from a starting node to all other nodes in a weighted graph

• It is often compared to breadth-first search, but Dijkstra’s includes edge weights and ensures the lowest total cost to reach each destination node

How It works:

• The graph is made up of nodes (vertices) and edges (arcs)

• Each edge has a weight, which can represent:

  • Time

  • Distance

  • Cost

• The algorithm explores all possible routes, keeping track of the shortest known distance to each node

• It guarantees the optimal path from the start node to every other node in the graph

• For revision on graphs, see section 18 - AI & Graphs

• An illustrated example of Dijkstra’s algorithm is shown below:

Performing Dijkstra's shortest path algorithm

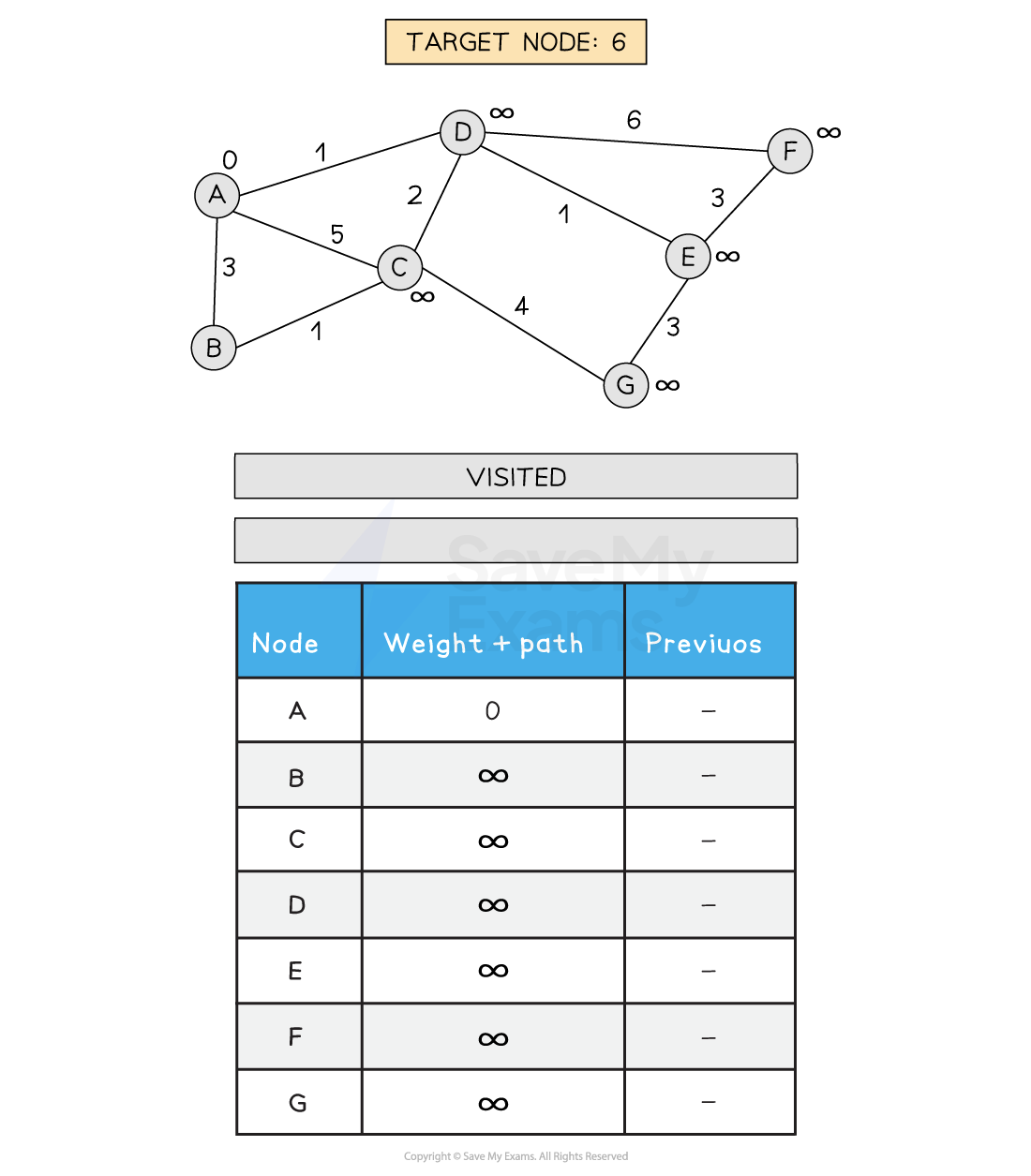
• Set A path to 0 and all other path weights to infinity

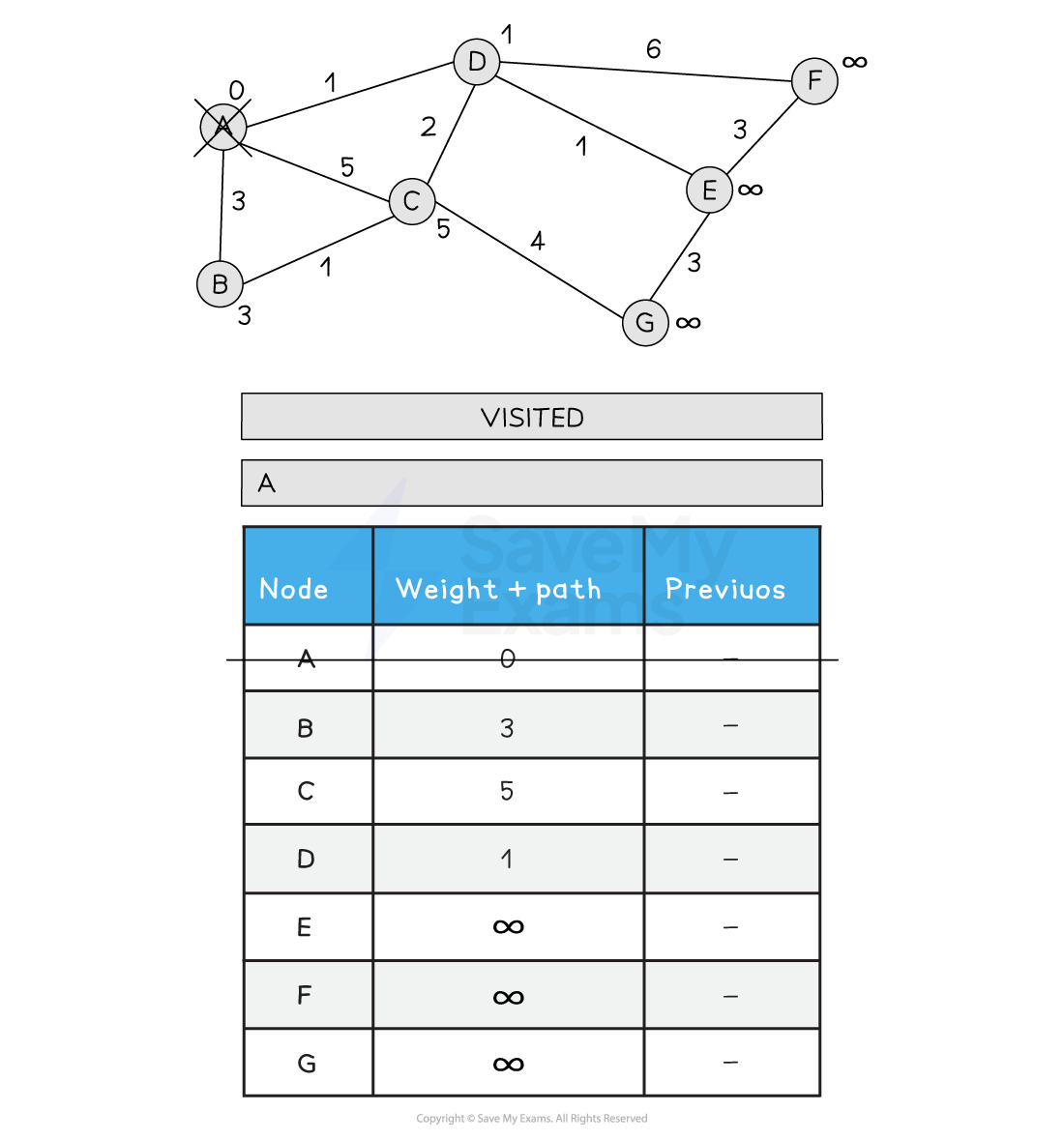
• Visit A. Update all neighbouring nodes path weights to the distance from A + A's path weight (0)

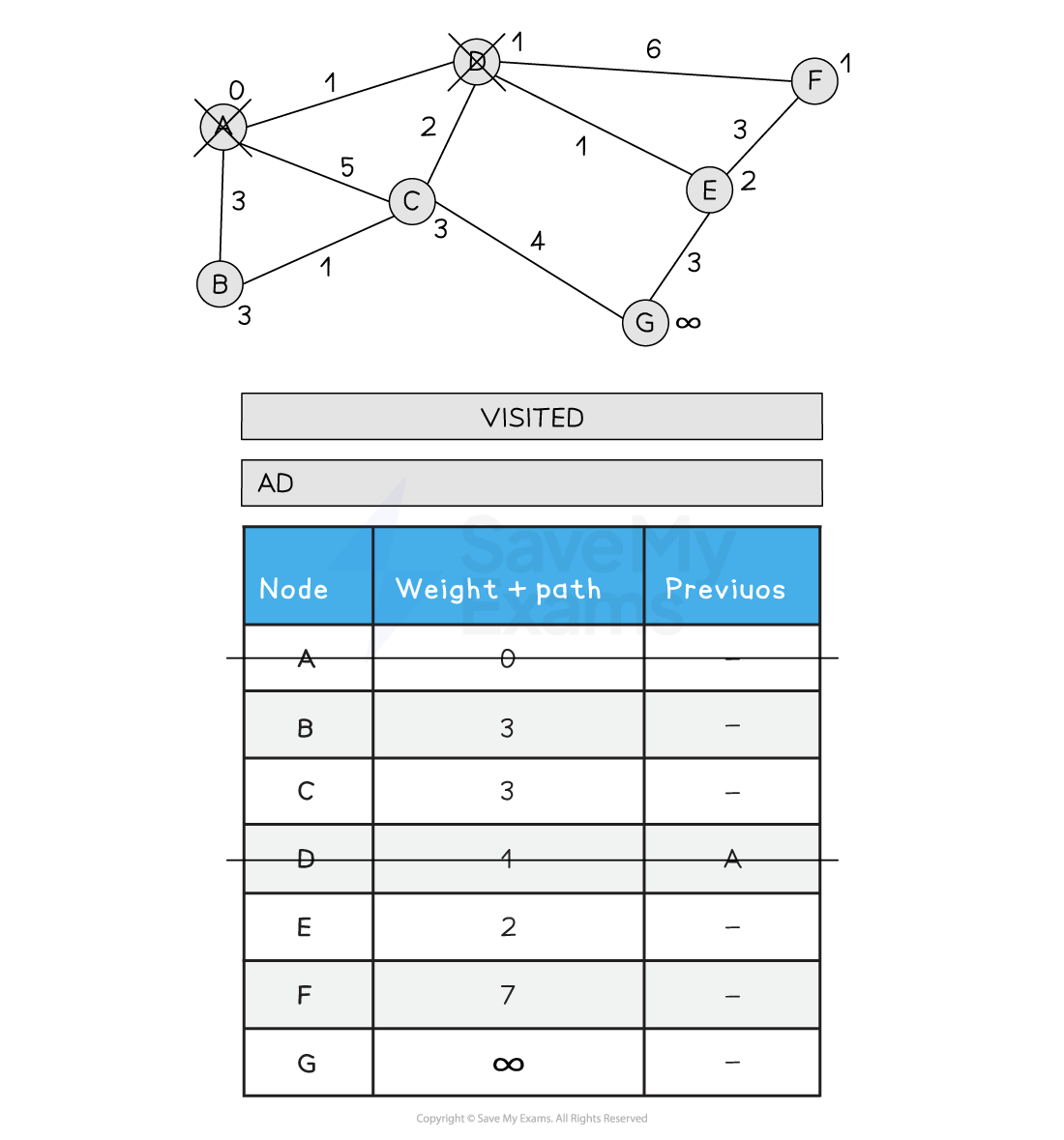
• Choose the next node to visit that has the lowest path weight (D)

• Visit D

• Update all neighbouring, non-visited nodes with a new path weight if the old path weight is bigger than the new path weight

• C is updated from 5 to 3 as the new path is shorted (A > D > C)

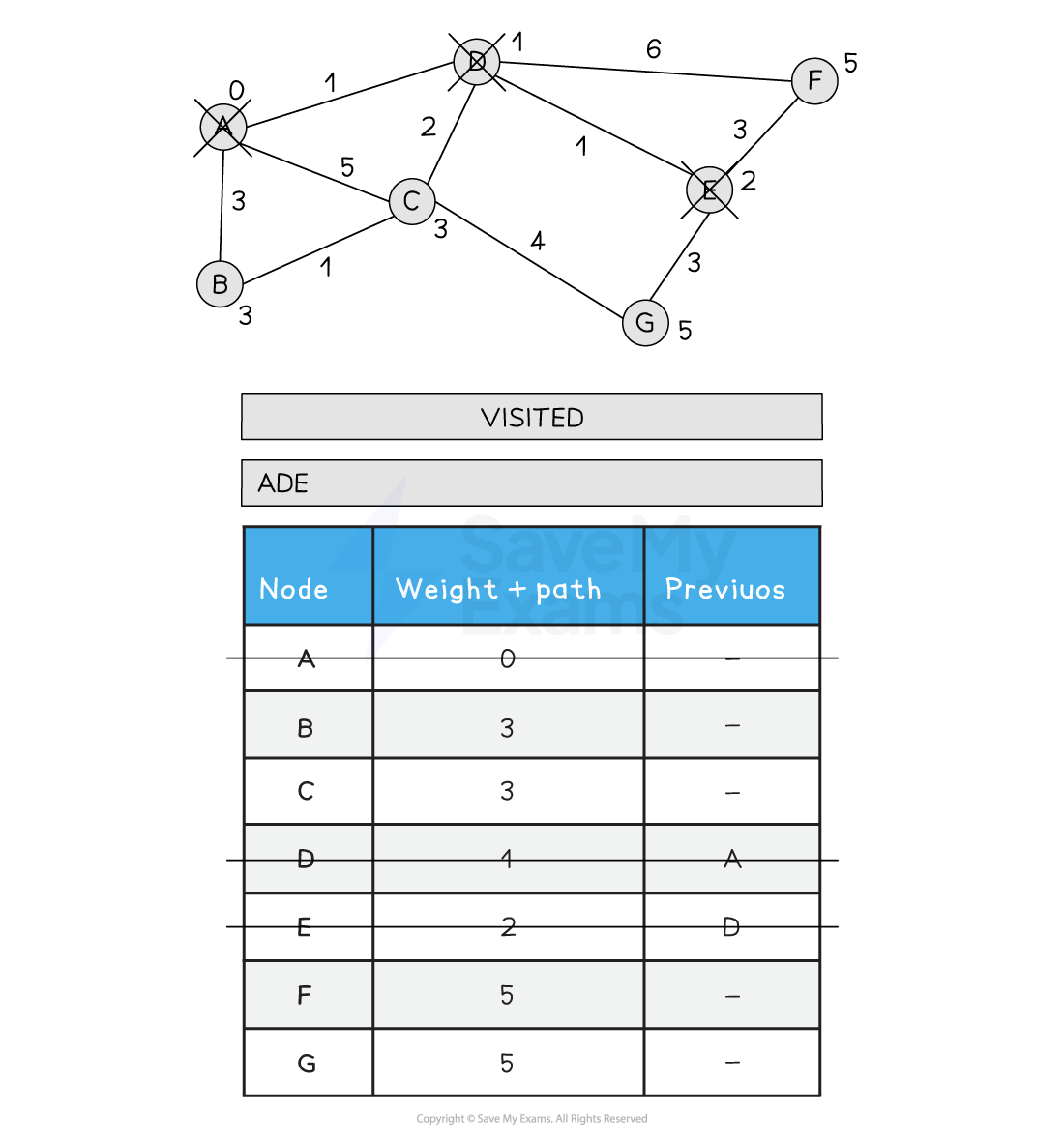
• Choose the next node to visit that has the lowest path weight (E)

• Visit E

• Update all neighbouring, non-visited nodes from E with a new path weight

• F is updated from 7 to 5 as the new path is shorter (A > D > E > F)

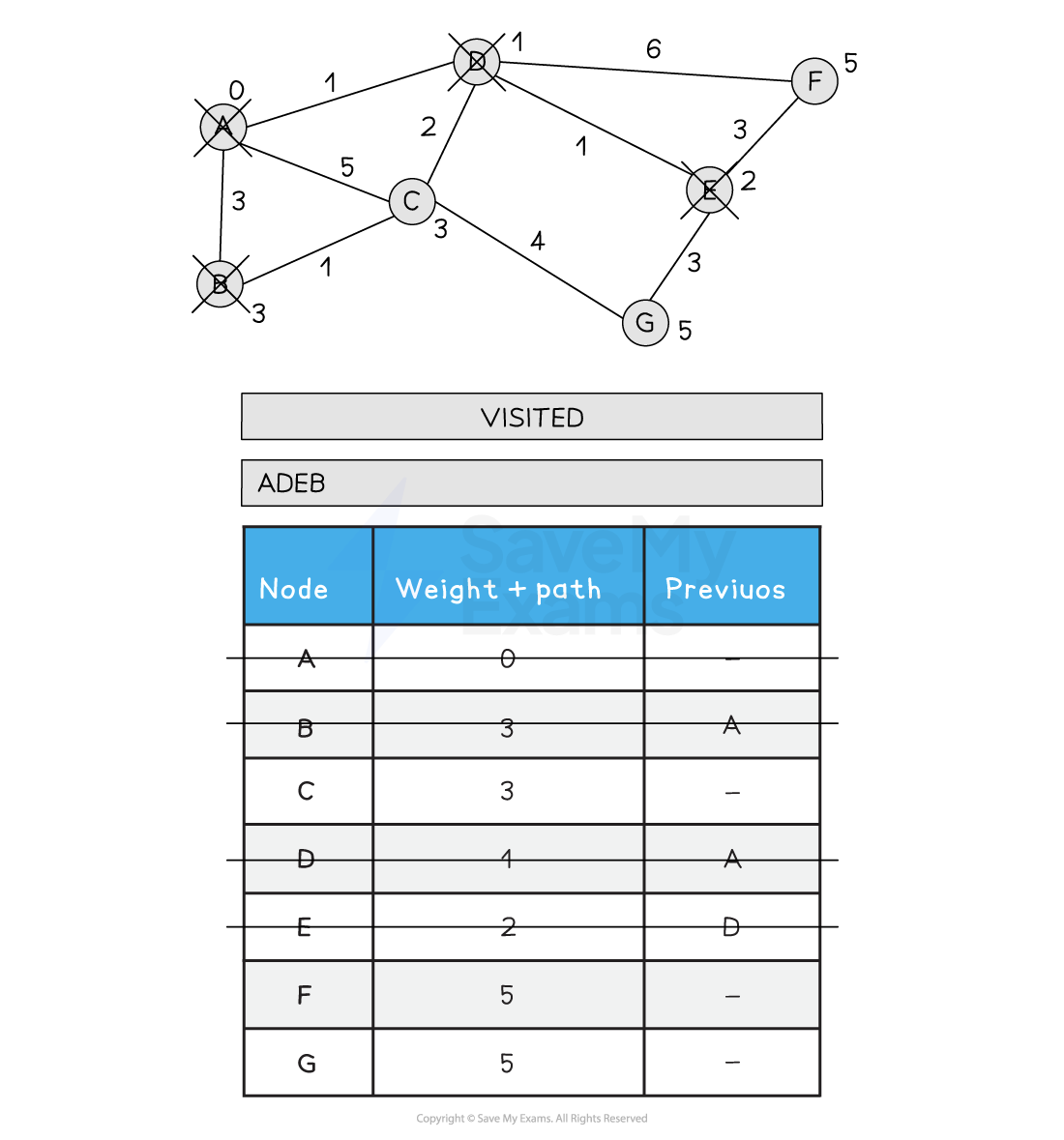
• Choose the next node to visit, alphabetically (B)

• Visit B

• Update all neighbouring non-visited nodes from B with a new weight if the path is less than the current path

• C is not updated as A > B > C is 4

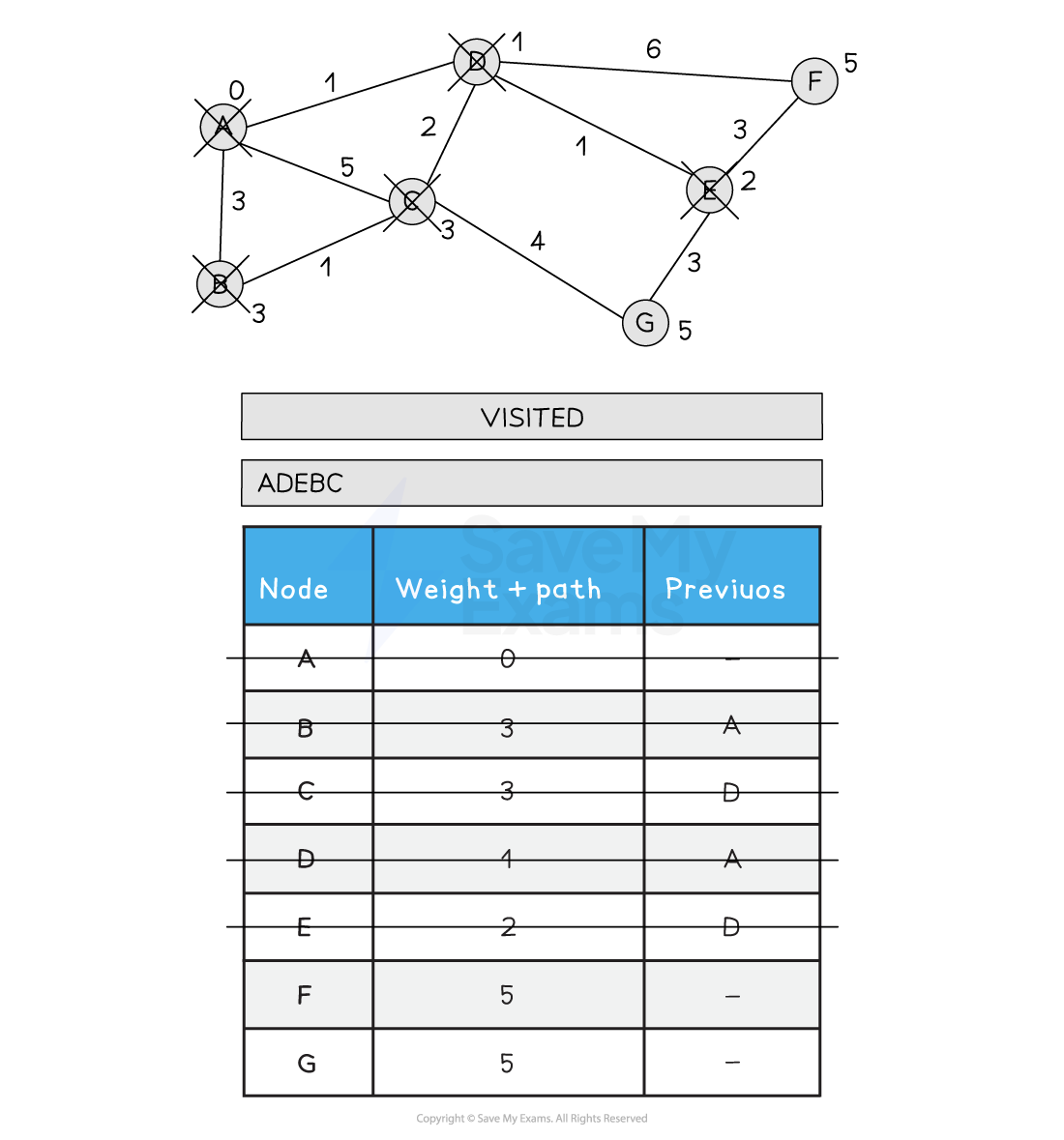
• Choose the next lowest node and visit (C)

• Update C's neighbours if the new path is shorter than the old path

• A > D > C > G is 8, so G is not updated

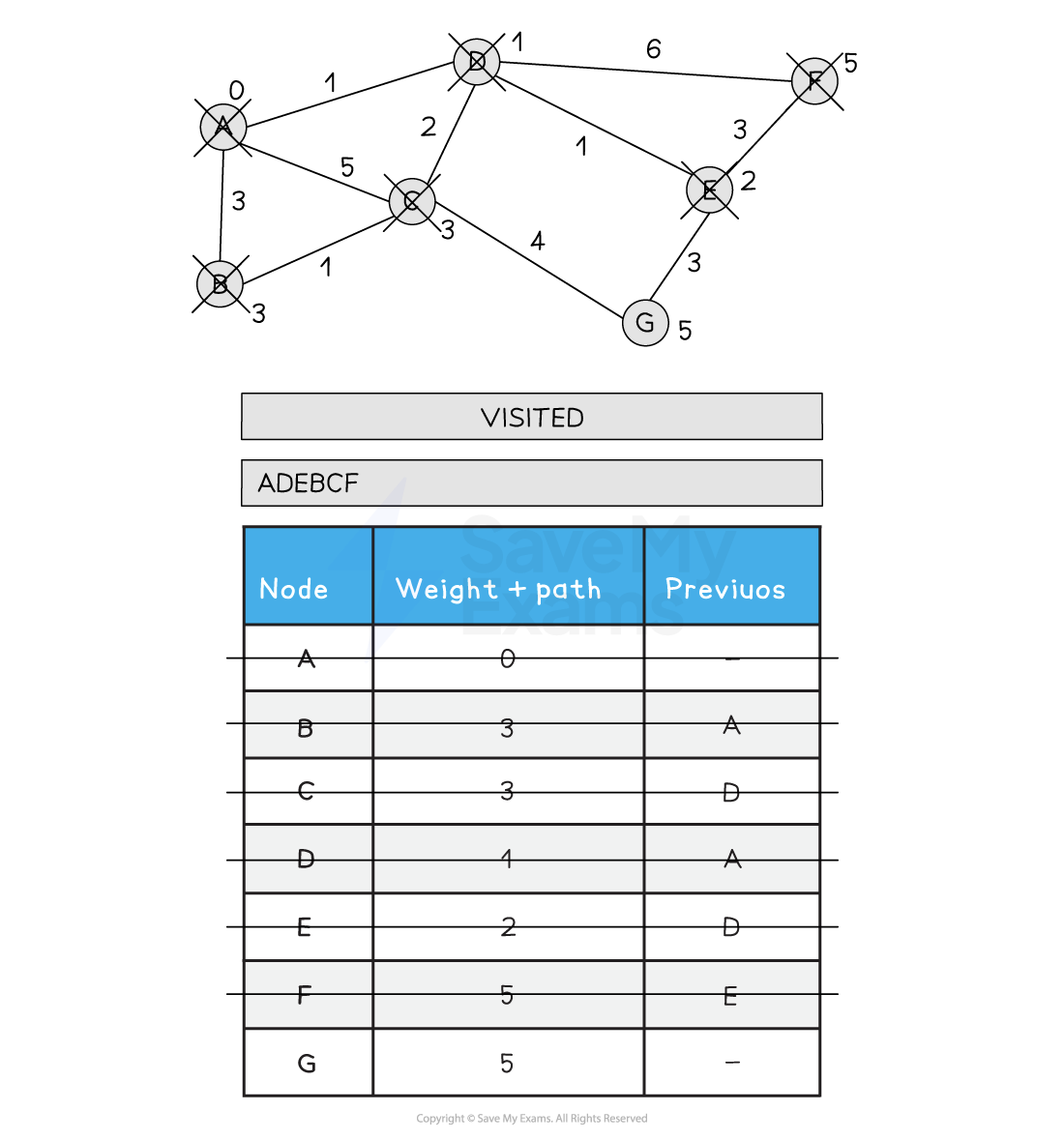
• Choose the next lowest node and visit (F)

• Update F's neighbours if the new path is shorter than the old path

• F has no non-visited neighbours so no updates are made

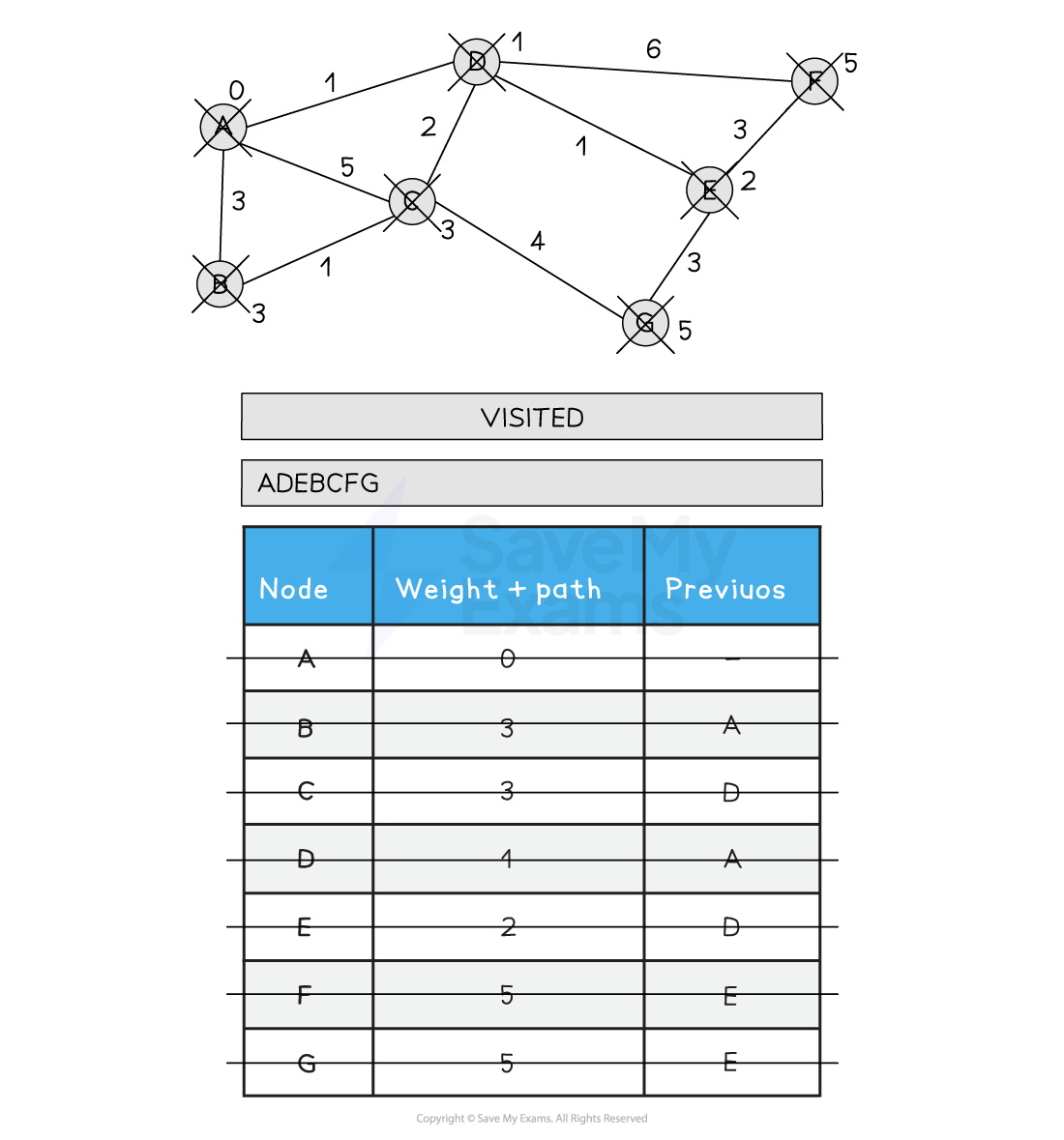
• Choose the next lowest node and visit (G)

• G has no non-visited neighbours so no updates are made

• All nodes have been visited

• Back tracking from G gives the following order and total distance A-D-E-G (5)

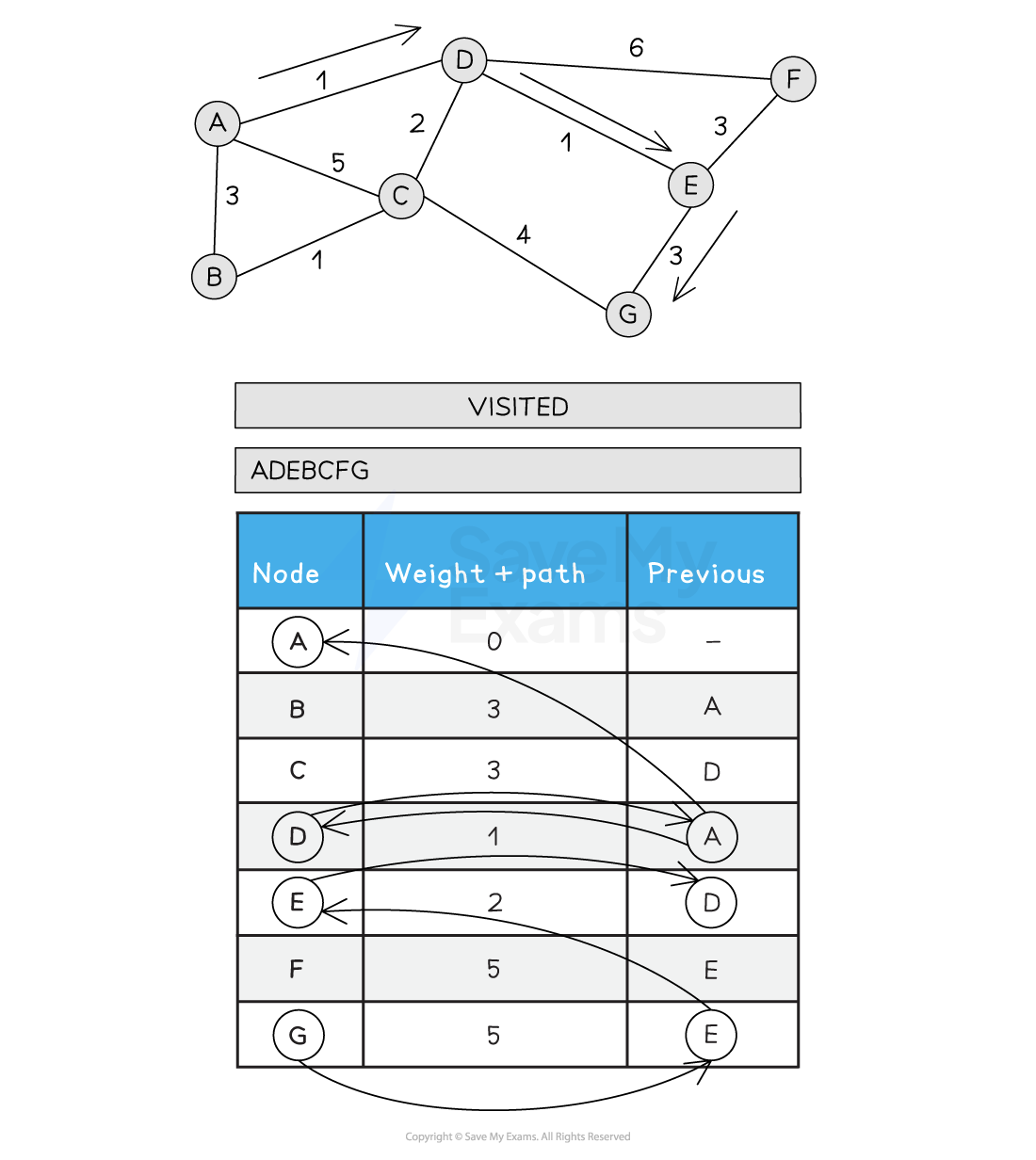
Figure 1: Performing Dijkstra’s Shortest path Algorithm

Programming Dijkstra's shortest path algorithm

How do you write Dijkstra's shortest path algorithm?

Pseudocode

FUNCTION Dijkstra(graph, start, goal)

    // Initialise distances
    FOR EACH node FROM graph
        SET distance[node] TO infinity
    NEXT node

    SET distance[start] TO 0
    DECLARE previousNode AS DICTIONARY
    DECLARE visited AS LIST
    DECLARE unvisited AS LIST

    FOR EACH node FROM graph
        ADD node TO unvisited
    NEXT node

    WHILE LENGTH(unvisited) > 0

        // Find unvisited node with shortest distance
        SET min TO null
        FOR EACH node FROM unvisited
            IF min = null THEN
                SET min TO node
            ELSEIF distance[node] < distance[min] THEN
                SET min TO node
            ENDIF
        NEXT node

        // Exit if goal reached
        IF min = goal THEN
            EXIT WHILE
        ENDIF

        // Update distances to neighbours
        FOR EACH neighbour FROM graph[min]
            SET cost TO weight(min, neighbour)  // assume this function returns the edge weight
            SET alt TO distance[min] + cost

            IF alt < distance[neighbour] THEN
                SET distance[neighbour] TO alt
                SET previousNode[neighbour] TO min
            ENDIF
        NEXT neighbour

        REMOVE min FROM unvisited
        ADD min TO visited

    ENDWHILE

    // Build path from goal to start
    DECLARE path AS LIST
    SET node TO goal

    WHILE node != start
        ADD node TO path
        SET node TO previousNode[node]
    ENDWHILE

    ADD start TO path
    REVERSE path

    RETURN path

ENDFUNCTION

Assumptions:

• graph[node] returns a list of neighbour nodes

• weight(x, y) returns the edge weight between node x and y

• Lists like visited, unvisited, and path support ADD and REMOVE

Python

def dijkstra(graph, start, goal):
    # Initialise distances and previous node map
    distance = {node: float('inf') for node in graph}
    distance[start] = 0
    previous_node = {}
    visited = set()
    unvisited = set(graph.keys())

    while unvisited:
        # Find the unvisited node with the smallest distance
        min_node = None
        for node in unvisited:
            if min_node is None or distance[node] < distance[min_node]:
                min_node = node

        if min_node == goal:
            break

        for neighbour, weight in graph[min_node]:
            if neighbour in visited:
                continue

            alt = distance[min_node] + weight
            if alt < distance[neighbour]:
                distance[neighbour] = alt
                previous_node[neighbour] = min_node

        visited.add(min_node)
        unvisited.remove(min_node)

    # Reconstruct path from goal to start
    path = []
    current = goal
    while current != start:
        path.append(current)
        current = previous_node[current]
    path.append(start)
    path.reverse()

    return path

Example usage:

# Graph format: adjacency list with weighted edges
graph = {
    'A': [('B', 2), ('C', 5)],
    'B': [('D', 1)],
    'C': [('D', 2)],
    'D': [('E', 3)],
    'E': []
}

print(dijkstra(graph, 'A', 'E'))

Output:

• A list of nodes representing the shortest path from 'A' to 'E'