Algorithm Analysis (Cambridge (CIE) A Level Computer Science): Revision Note

Suitability of algorithms

Why do we need to check the suitability of algorithms?

• Algorithms must be compared to determine how suitable they are for solving a specific problem or working with a particular set of data

• Key factors in comparing algorithms include:

  • How long they take to complete a task (time complexity)

  • How much memory they require to complete a task (space complexity)

• Generally, the most suitable algorithm is the one that solves the problem in the shortest time and using the least memory

Time complexity

• Time complexity refers to the number of operations or steps an algorithm takes to complete, not the actual time in seconds or minutes

• It is important to understand that time complexity is independent of hardware performance

• A faster CPU may execute instructions more quickly, but the number of instructions the algorithm performs remains the same

Analogy: Running a marathon

• The marathon distance = the algorithm

• The runners = different CPUs

• Each runner finishes at a different time, but the distance (number of steps) is the same

Space complexity

• Space complexity refers to the amount of memory an algorithm needs to complete its task

• Memory usage includes:

  • Space for input data

  • Temporary variables

  • Any additional data structures (e.g. arrays, stacks, queues)

• For example:

  • If an algorithm creates a new copy of the input data, it will require more memory than one that modifies the data in place

  • An algorithm that uses recursion may use more memory due to the call stack

Big O Notation

What is Big O Notation?

• Big O Notation is a mathematical way to describe the time and space complexity of an algorithm

• It shows how well an algorithm scales as the size of the input increases

  • It describes the order of growth (efficiency) of an algorithm

  • It is hardware-independent – it measures steps or operations, not seconds

  • Named after German mathematician Edmund Landau

Big O Rules:

1. Keep only the dominant term (largest exponent or growth rate)

2. Ignore constants – they become insignificant as input size grows

Types of time complexity

O(1) – Constant time

• The algorithm always takes the same number of steps, regardless of input size

totalLength = len(s)

• The length is returned in one step, even if the string is very long

O(n) – Linear time

• The number of steps increases proportionally with the input size n

function sumNumbers1(n)
    sum = 0
    for i = 1 to n
        sum = sum + i
    next i
    return sum
endfunction

• For input size n, the algorithm performs n + 1 steps

• Example with multiple loops:

function loop
    x = input
    for i = 1 to x
        print(x)
    next i

    a = 0
    for j = 1 to x
        a = a + 1
    next j
    print(a)

    b = 1
    for k = 1 to x
        b = b + 1
    next k
    print(b)
endfunction

• Total steps = 3x + 5 ⇒ Still O(n) as x grows

O(n^2) – Polynomial time

• Performance is proportional to the square of the input size

• Caused by nested loops

function timesTable
    x = 12
    for i = 1 to x
        for j = 1 to x
            print(i, " x ", j, " = ", i*j)
        next j
    next i

    for k = 1 to x
        print(k)
    next k

    print("Hello World!")
endfunction

• Steps: x^2 + x + 2 ⇒ Dominant term is x^2 ⇒ O(n^2)

• As x increases, the impact of lower-order terms and constants becomes negligible

O(log n) – Logarithmic time

• The number of steps grows slowly even as input size grows rapidly

• Common in binary search

  • Example: log2(8) = 3, because 2^3 = 8

  • Doubling input size barely affects total steps

• Very efficient – useful for large datasets

O(2^n) – Exponential time

• The number of steps doubles for every additional input value

• Grows extremely fast

• Very inefficient, but some problems (e.g. brute-force solutions) fall into this category

• Rare in practice unless necessary

O(n log n) – Linear logarithmic time

• Algorithms that divide data and process each part

• Example: Merge Sort

• More efficient than O(n^2), commonly used in sorting

Best, average, and worst case

• Every algorithm has different performance depending on input:

• Big O notation usually describes the worst-case performance to guarantee a minimum standard

How to derive Big O from code

1. Count loops:

   • 1 loop = O(n)

   • 2 nested loops = O(n^2)

   • No loops = O(1)

2. Ignore constants and lower-order terms:

   • 3n^2 + 4n + 5 → O(n^2)

Examples

function sumNumbers1(n)
    sum = 0
    for i = 1 to n
        sum = sum + i
    next i
    return sum
endfunction

• One loop → O(n)

function sumNumbers2(n)
    sum = n * (n + 1) / 2
    return sum
endfunction

• One statement → O(1)

function loop
    (3 loops, 5 statements)
    ⇒ O(n)
endfunction

function timesTable
    (nested loop + 1 loop + 1 statement)
    ⇒ O(n^2)
endfunction

Time complexity graph

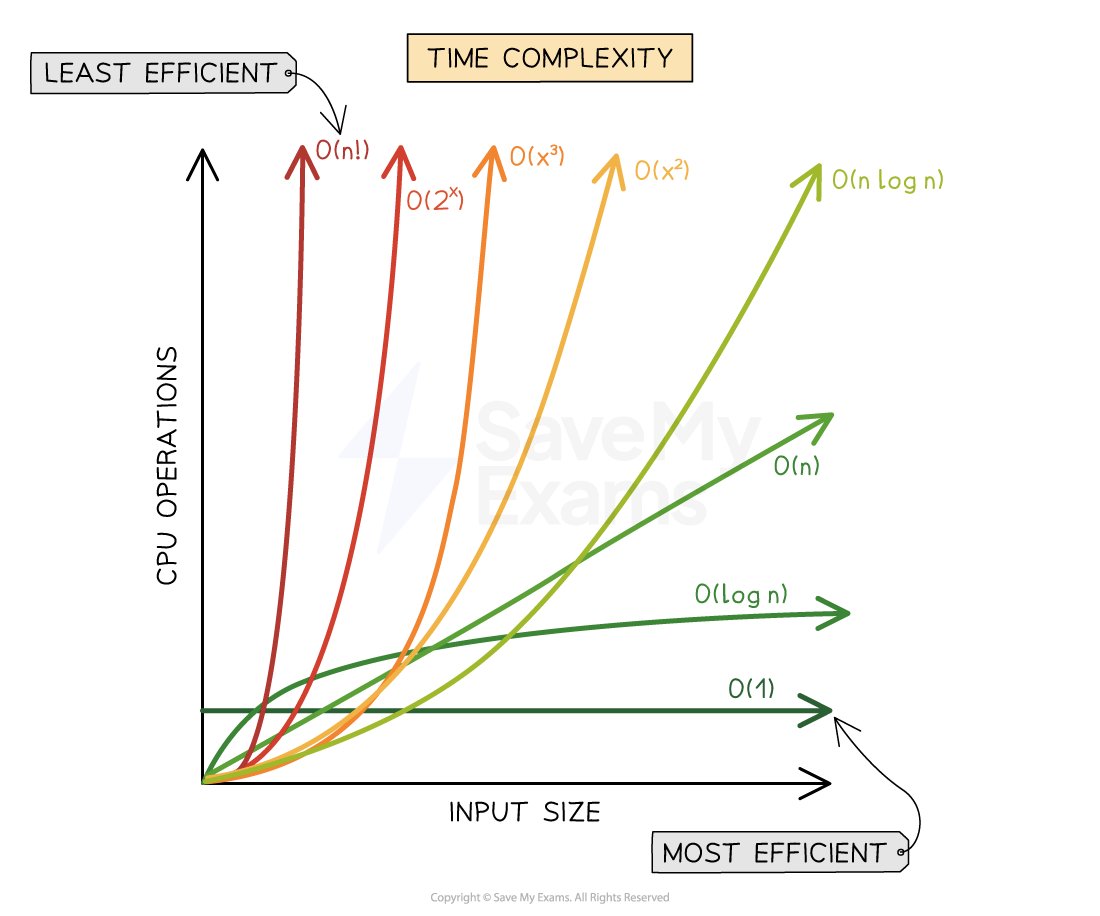
• From the graph, exponential time (2ⁿ) grows the quickest and therefore is the most inefficient form of algorithm, followed by polynomial time (n²), linear time (n), logarithmic time (logn) and finally constant time (1)

• Further time complexities exist such as factorial time (n!) which performs worse than exponential time and linear-logarithmic time (nlogn) which sits between polynomial and linear time. Merge sort is an example of an algorithm that uses O(nlogn) time complexity

• The Big-O time complexity of an algorithm can be derived by inspecting its component parts

• It is important to know that when determining an algorithm's Big-O that only the dominant factor is used.

• This means the time complexity that contributes the most to the algorithm is used to describe the algorithm. For example:

  • 3x² + 4x + 5, which describes three nested loops, four standard loops and five statements is described as O(n²)

  • x² is the dominating factor. As the input size grows x² contributes proportionally more than the other factors

  • Coefficients are also removed from the Big-O notation. The 3 in 3x² acts as a multiplicative value whose contribution becomes smaller and smaller as the size of the input increases.

    • For an arbitrarily large value such as 10¹⁰⁰, which is 10 with one hundred 0’s after it, multiplying this number by 3 will have little contribution to the overall time complexity. 3 is therefore dropped from the overall time complexity