Binary Search (Cambridge (CIE) A Level Computer Science): Revision Note

Binary search

What is a binary search?

• The binary search is a more efficient search method than linear search

• The binary search compares the middle item to the searched for target item. If the values match then the index is returned. If not then the list is adjusted such that:

  •  the top half is ignored if the target item is less than the middle value

  • or the bottom half is ignored if the target item is larger than the middle value

• Once the list has been adjusted, the search continues until the item is found or the item is not in the list

• It is important to note that the list must be sorted for the binary search to work correctly

• The implementation of the binary search is shown below

Performing the binary search

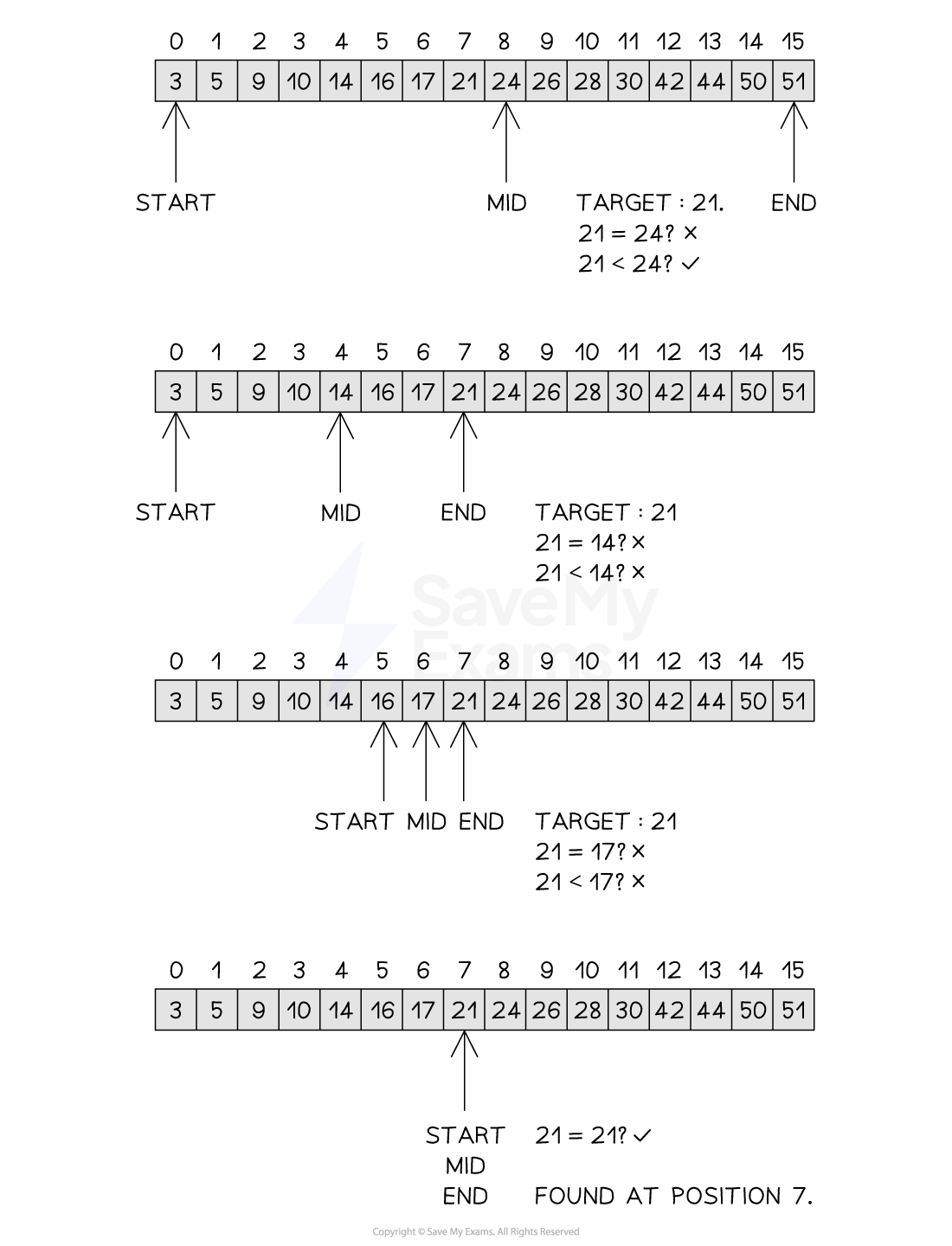
Figure 2: Performing the Binary Search

Time complexity of a binary search

• The binary search is an example of a logarithmic time complexity O(logn) as it halves the search space with each iteration of the while loop. This approach is known as divide and conquer, where a problem is progressively reduced in size such that when each problem is at its smallest it is easiest to solve

• The algorithm starts with n items before the first iteration. After the first there are n/2 items, after the second there are n/4 items, after the third there are n/8 items and so on, leading to n/2ⁱ after i iterations

• The worst case scenario or maximum number of iterations to find one item is where n/2ⁱ = 1

  • Multiply both sides by 2ⁱ to get: n = 2ⁱ

  • Take the logarithm of both sides: logn = log2ⁱ

  • Rewrite with i at the front (using laws of logarithms): logn = ilog2

  • Log2 (assuming a base of 2 is used) becomes 1, giving: logn = i

  • The binary search is therefore O(logn)

• The best case scenario would be O(1) where the item is found on the first comparison, while the average case would be O(logn/2) which would find the item somewhere in the middle of the search. Removing coefficients means the average case would therefore still be O(logn)

Space complexity of a binary search

• As the binary search requires no additional space, it is space complexity O(n), where n is the number of items in the list

Tracing a binary search

• Given the following list [3, 5, 9, 10, 14, 16, 17, 21, 24, 26, 28, 30, 42, 44, 50, 51], a trace table for the binary search is shown below

Trace Table for the Binary Search

Implementing a binary search

Pseudocode

FUNCTION binarySearch(list : ARRAY OF INTEGER, item : INTEGER) RETURNS INTEGER
    DECLARE found : BOOLEAN
    DECLARE index : INTEGER
    DECLARE start : INTEGER
    DECLARE end : INTEGER
    DECLARE mid : INTEGER

    found ← FALSE
    index ← -1
    start ← 0
    end ← LENGTH(list) - 1

    WHILE start <= end AND found = FALSE
        mid ← (start + end) DIV 2

        IF list[mid] = item THEN
            found ← TRUE
            index ← mid
        ELSE
            IF list[mid] < item THEN
                start ← mid + 1
            ELSE
                end ← mid - 1
            ENDIF
        ENDIF
    ENDWHILE

    RETURN index
ENDFUNCTION

• Function definition:
  FUNCTION binarySearch(list : ARRAY OF INTEGER, item : INTEGER) RETURNS INTEGER

  • The function searches a sorted array for a given item.

  • It returns the index of the item if found, or -1 if not found.

• Variable declarations:

  • found → a flag to indicate if the item is found (initially FALSE)

  • index → the result to be returned (initially -1)

  • start → index of the start of the current search range (initially 0)

  • end → index of the end of the current search range (initially LENGTH(list) - 1)

  • mid → index of the middle element in the current range

• Loop condition:
  WHILE start <= end AND found = FALSE

  • Keep searching while the search range is valid and the item hasn't been found.

• Middle element calculation:
  mid ← (start + end) DIV 2

  • Calculates the index of the middle element of the current search range.

• Check for match:
  IF list[mid] = item THEN

  • If the middle element is equal to the target item:

    • Set found ← TRUE

    • Store the index ← mid

• Adjust search range:

  • If the middle value is less than the item:

    • Search the right half → start ← mid + 1

  • Otherwise:

    • Search the left half → end ← mid - 1

• Loop ends:

  • The loop stops when the item is found or the search range becomes invalid.

• Return value:
  RETURN index

  • Returns the index if found, or -1 if not found

Python

def binary_search(list, item):
  found = False
  index = -1
  start = 0
  end = len(list) - 1

  while start <= end and not found:
    mid = (start + end) // 2
  if list[mid] == item:
    found = True
    index = mid
  elif list[mid] < item:
    start = mid + 1
  else:
    end = mid - 1

  return index

Java

public class BinarySearch {

    public static int binarySearch(int[] list, int item) {
        boolean found = false;
        int index = -1;
        int start = 0;
        int end = list.length - 1;

        while (start <= end && !found) {  // Corrected found condition
            int mid = (start + end) / 2;

            if (list[mid] == item) {
                found = true;
                index = mid;
            } else if (list[mid] < item) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }

        return index;
    }