Linear Search (Cambridge (CIE) A Level Computer Science): Revision Note
Exam code: 9618
Linear search
What is a linear search?
The linear search is a standard algorithm used to find elements in an unordered list
The list is searched sequentially and systematically from the start to the end one element at a time
Comparing each element to the value being searched for
If the value is found the algorithm outputs where it was found in the list
If the value is not found it outputs a message stating it is not in the list
An example of using a linear search would be looking for a specific student name in a list or searching for a supermarket item in a shopping list
Performing the linear search
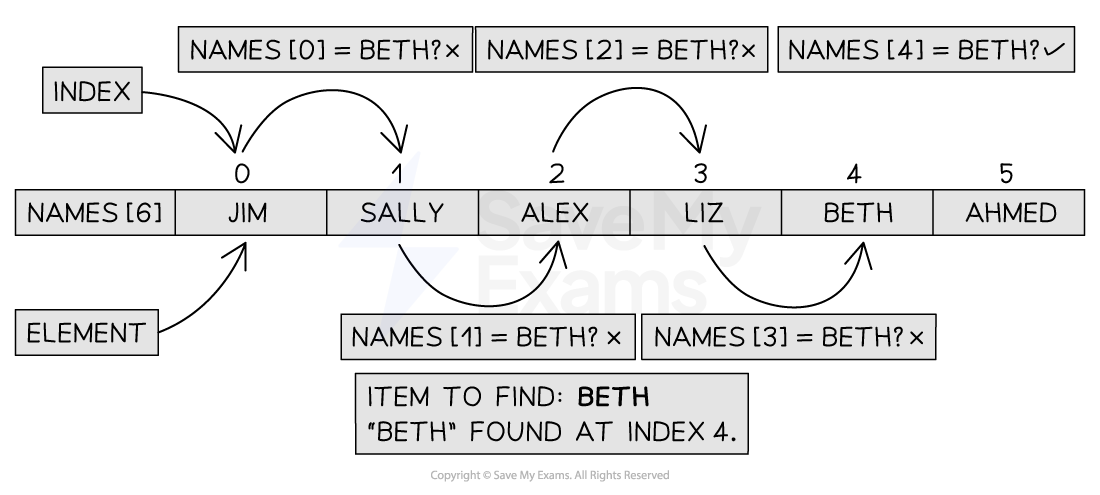
Figure 1: Performing the Linear Search
Time complexity of a linear search
To determine the algorithm's execution time as measured by the number of instructions or steps carried out, Big-O notation must be used
The loop is executed n times, once for each item. There are two instructions within the loop, the if statement and an assignment, hence the Big-O for the loop is O(2n)
There are three initial statements which are O(1)
The overall Big-O notation is therefore 2n + 3, which when coefficients are factored out, becomes O(n) as linear time dominates constant time. The constant term and coefficients contribute significantly less as the input size n grows larger
It is important to remember here that O(n) is the worst case scenario. The best case scenario O(1) would find the item the first time, while the average case would be O(n/2) which when we remove coefficients still becomes O(n)
Space complexity of a linear search
As the linear search requires no additional space, it is space complexity O(n) where n is the number of items in the list
Tracing a linear search
Given the following list [5, 4, 7, 1, 3, 8, 9, 2], a trace table for the linear search is shown below
Trace Table of the Linear Search
item | index | i | list[i] | found |
|---|---|---|---|---|
8 | -1 | 0 | 5 | False |
|
| 1 | 4 |
|
|
| 2 | 5 |
|
|
| 3 | 1 |
|
|
| 4 | 3 |
|
8 | 5 | 5 | 8 | True |
Implementing a linear search
Pseudocode
FUNCTION linearSearch(list : ARRAY OF STRING, item : STRING) RETURNS INTEGER
DECLARE index : INTEGER
DECLARE i : INTEGER
DECLARE found : BOOLEAN
index ← -1
i ← 0
found ← FALSE
WHILE i < LENGTH(list) AND found = FALSE
IF list[i] = item THEN
index ← i
found ← TRUE
ENDIF
i ← i + 1
ENDWHILE
RETURN index
ENDFUNCTIONFunction definition:
FUNCTION linearSearch(list : ARRAY OF STRING, item : STRING) RETURNS INTEGERThe function takes a list and a target item.
It returns the index of the item if found, or -1 if not.
Variable declarations:
index,i, andfoundare declared:indexstores the result (default is -1 if not found).iis the loop counter.foundis a boolean used to stop the search once the item is found.
Initialisation:
index ← -1→ start with "not found"i ← 0→ start from the first index of the listfound ← FALSE→ the item hasn’t been found yet
Loop condition:
WHILE i < LENGTH(list) AND found = FALSEContinue looping while there are items left to check and the item hasn’t been found.
Comparison inside loop:
IF list[i] = item THENCheck if the current element equals the search item.
If a match is found:
index ← i→ save the current indexfound ← TRUE→ stop searching
Increment:
i ← i + 1→ move to the next item
End of loop:
Once the loop finishes (either item is found or end of list is reached), return the result.
Return value:
RETURN indexReturns the index where the item was found.
If it wasn’t found, it returns
-1.
Python
def linear_search(list, item):
index = -1
for i in range(len(list)):
if list[i] == item:
index = i
break # Stop the loop once the item is found
return indexJava
public class LinearSearch {
public static int linearSearch(int[] list, int item) {
int index = -1;
for (int i = 0; i < list.length; i++) {
if (list[i] == item) {
index = i;
break; // Stop the loop once the item is found
}
}
return index;
}
Unlock more, it's free!
Did this page help you?