The Poisson Distribution (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Properties of Poisson Distribution
What is a Poisson distribution?
A Poisson distribution is a discrete probability distribution
The discrete random variable
follows a Poisson distribution if it counts the number of events that occur at random in a given time or space
For a Poisson distribution to be valid it must satisfy the following properties:
Events occur singly and at random in a given interval of time or space
The mean number of occurrences in the given interval(λ) is known and finite
λ has to be positive but does not have to be an integer
Each occurrence is independent of the other occurrences
If
follows a Poisson distribution then it is denoted
is the mean number of trials
The formula for the probability of r occurrences in a given interval is:
for r=0, 1, 2, .....,
e is the constant 2.718…
What are the important properties of a Poisson distribution?
The mean and variance of a Poisson distribution are roughly equal
The distribution can be represented visually using a vertical line graph
If λ is close to 0 then the graph has a tail to the right (positive skew)
If λ is at least 5 then the graph is roughly symmetrical
The Poisson distribution becomes more symmetrical as the value of the mean (λ) increases

Worked Example
is the random variable ‘The number of cars that pass a traffic camera per day’. State the conditions that would need to be met for
to follow a Poisson distribution.

Did this video help you?
Modelling with Poisson Distribution
How do I set up a Poisson model?
Find the mean and variance and check that they are roughly equal
You may have to change the mean depending on the given time/space interval
Make sure you clearly state what your random variable is
For example, let X be the number of typing errors per page in an academic article
Identify what probability you are looking for
What can be modelled using a Poisson distribution?
Anything that occurs singly and randomly in a given interval of time or space and satisfies the conditions
For example, let X be the random variable 'the number of emails that arrive into your inbox per day'
There is a given interval of a day, this is an example of an interval of time
We can assume the emails arrive into your inbox at random
We can assume each email is independent of the other emails
This is something that you would have to consider before using the Poisson distribution as a model
If you know the mean number of emails per day a Poisson distribution can be used
Sometimes the given interval will be for space
For example, the number of daisies that exist on a square metre of grass
look carefully at the units given as you may have to change them when calculating probabilities
Worked Example
State, with reasons, whether the following can be modelled using a Poisson distribution and if so write the distribution.
(i) Faults occur in a length of cloth at a mean rate of 2 per metre.
(ii) On average 4% of a certain population has green eyes.
(iii) An emergency service company receives, on average, 15 calls per hour.

Examiner Tips and Tricks
If you are asked to criticise a Poisson model always consider whether the trials are independent, this is usually the one that stops a variable from following a Poisson distribution!
Did this video help you?
Calculating Poisson Probabilities
Throughout this section we will use the random variable . For a Poisson distribution, the probability of a X taking a non-integer or negative value is always zero. Therefore any values mentioned in this section (other than λ) will be assumed to be non-negative integers.
Where does the formula for a Poisson distribution come from?
The formula for calculating an individual Poisson probability is
for r = 0, 1, 2 ,....
The derivation of the formula comes from the binomial distribution, however it is outside the scope of this syllabus and will not be proved here
Whilst the binomial distribution relies on knowing a fixed number of trials, the Poisson can allow for any number of trials within a time period
Only the mean number of occurrences of an event within the given period needs to be known
How do I calculate the cumulative probabilities for a Poisson distribution?
To find an individual probability use the formula
Most of the time you will be required to calculate cumulative Poisson probabilities rather than individual ones
Use the formula to find the individual probabilities and then add them up
Make sure you are confident working with inequalities for discrete values
Only integer values will be included so it is easiest to look at which integer values you should include within your calculation
Sometimes it is quicker to find the probabilities that are not being asked for and subtract from one
is asking you to find the probabilities of all values up to and including x
This means all values that are at most x
Don’t forget to include P(X = 0)
is asking you to find the probabilities of all values up to but not including x
This means all values that are less than x
Stop at x-1
is asking you to find the probabilities of all values greater than and including x
This means all values that are at least x
As there is not a fixed number of trials this includes an infinite number of possibilities
To calculate this, use the identity
is asking you to find the probabilities of all values greater than but not including x
This means all values that are more than x
Rewrite
as to calculate this
If calculating
pay attention to whether the probability of a and b should be included in the calculation or not
For example,
:
You want the integers 5 to 10
How can calculating probabilities for a Poisson distribution be made easier?
Having to type a lot of calculations into your calculator can be time consuming and cause errors
Consider the calculation
Note that
exists in every term and can be factorised out
Recall that
and 0! = 1
Recall also that
and 1! = 1
This calculation could be factorised and simplified to
This is much simpler and easier to type into your calculator in exam conditions
How do I change the mean for a Poisson distribution?
Sometimes the mean may be given for a different interval of time or space than that which you need to calculate the probability for
A given value of λ can be adjusted to fit the necessary time period
For example if a football team score a mean of 2 goals an hour and we want to find the probability of them scoring a certain number of goals in a 90 minute game, then we would use the distribution X ~ Po(3)
90 = 1.5 (60) so use 1.5λ
A very useful property of the Poisson distribution is that if X and Y are two independent Poisson distributions then their sums, X + Y is also a Poisson distribution
If X ~ Po(λ) and Y ~ Po(μ) then X + Y ~ Po(λ + μ)
Note that, for an integer value of a and b greater than 1, aX + bY no longer follows a Poisson distribution
Worked Example
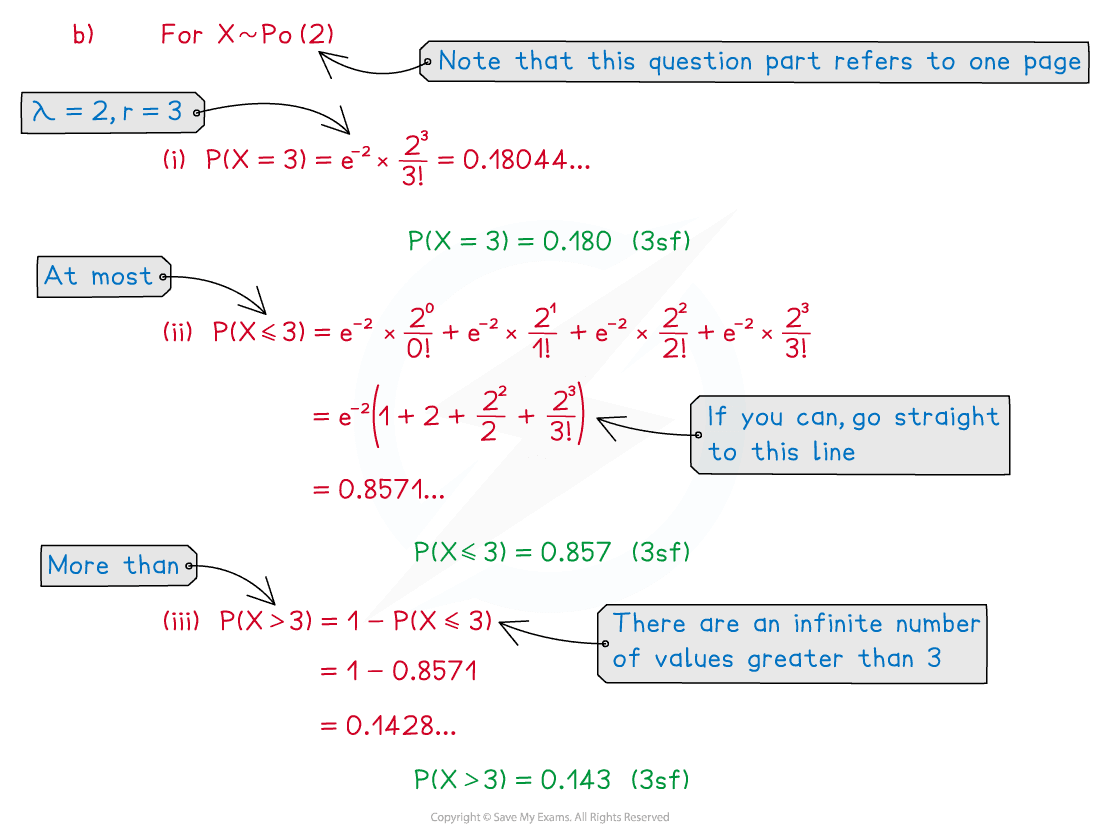
Xiao makes silly mistakes in his maths homework at a mean rate of 2 per page.
(a) Define a suitable distribution to model the number of silly mistakes Xiao would make in a piece of homework that is five pages long. State any assumptions you have made.

(b) Find the probability that in any random page of Xiao’s homework book there are
(i) exactly three silly mistakes
(ii) at most three silly mistakes
(iii) more than three silly mistakes.
Examiner Tips and Tricks
Look carefully at the given time or space interval to check if you need to change the mean before carrying out calculations. Be prepared for this to change between question parts!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?