Geometric Series (Edexcel International AS Maths): Revision Note

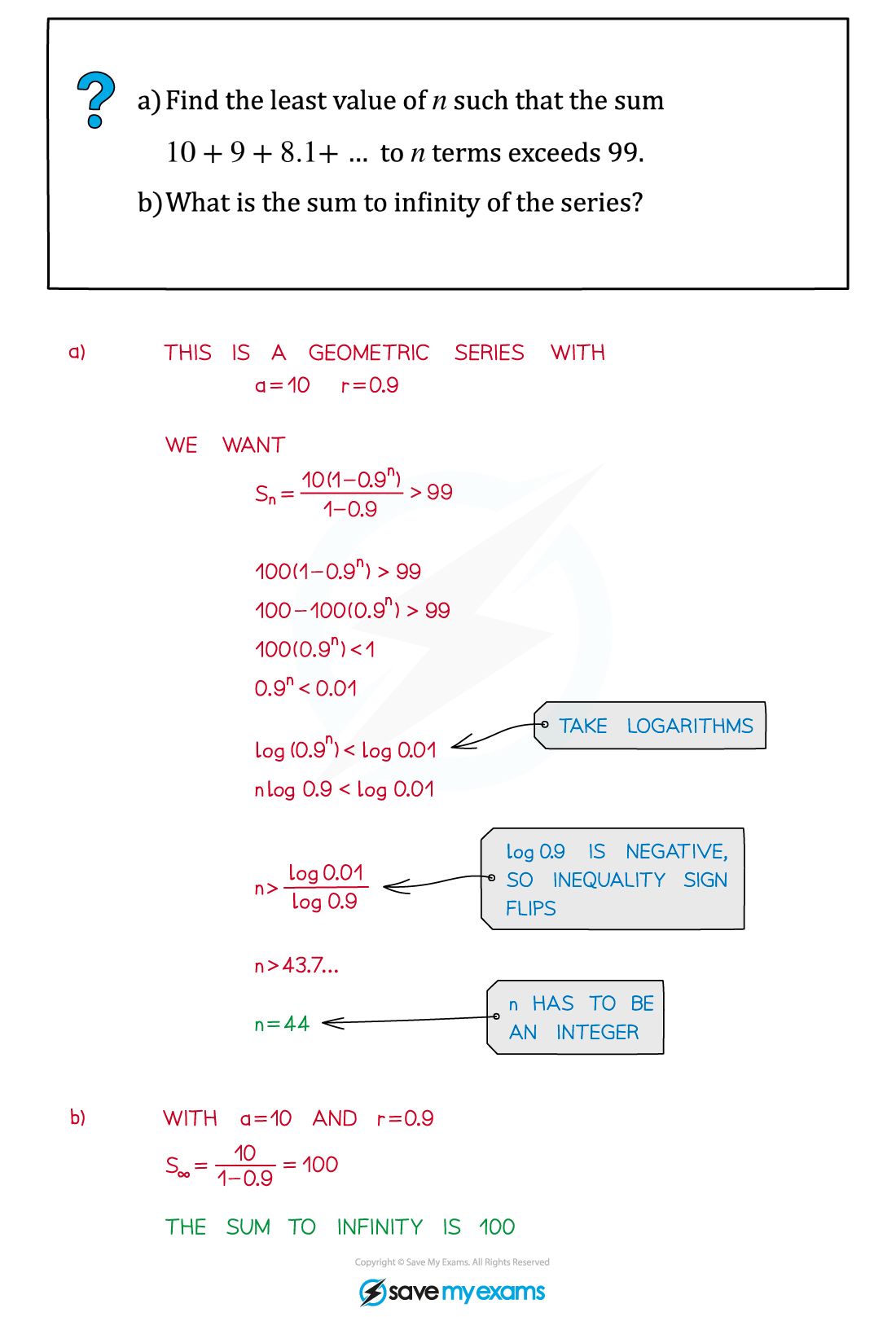
Geometric series

How do I find the sum of a geometric series?

• A geometric series is the sum of the terms of a geometric sequence

• The following formulae will let you find the sum of the first n terms of a geometric series:

     or   

  • a is the first term

  • r is the common ratio

• The one on the left is more convenient if r < 1, the one on the right is more convenient if r > 1

• The a and the r in those formulae are exactly the same as the ones used with geometric sequences

How do I prove the geometric series formula?

• Learn this proof of the geometric series formula – you can be asked to give it in the exam:

  • Write out the sum once

  • Write out the sum again but multiply each term by r

  • Subtract the second sum from the first

    • All the terms except two should cancel out

  • Factorise and rearrange to make S the subject

What is the sum to infinity of a geometric series?

• If (and only if!) |r| < 1, then the geometric series converges to a finite value given by the formula

•  S_∞ is known as the sum to infinity

• If |r| ≥ 1 the geometric series is divergent and the sum to infinity does not exist