Revision NotesExam QuestionsPast PapersMock Exams
International ASMathsEdexcelPure 2Revision NotesTrigonometryTrigonometric EquationsSimple Trigonometric Identities

Simple Trigonometric Identities (Edexcel International AS Maths): Revision Note

Exam code: XMA01

Lucy Kirkham

Last updated

Simple trigonometric identities

What is a trigonometric identity?

  • Trigonometric identities are statements that are true for all values of x or theta (θ)

  • They are used to help simplify trig equations before solving them

  • The first two identities you must know are:

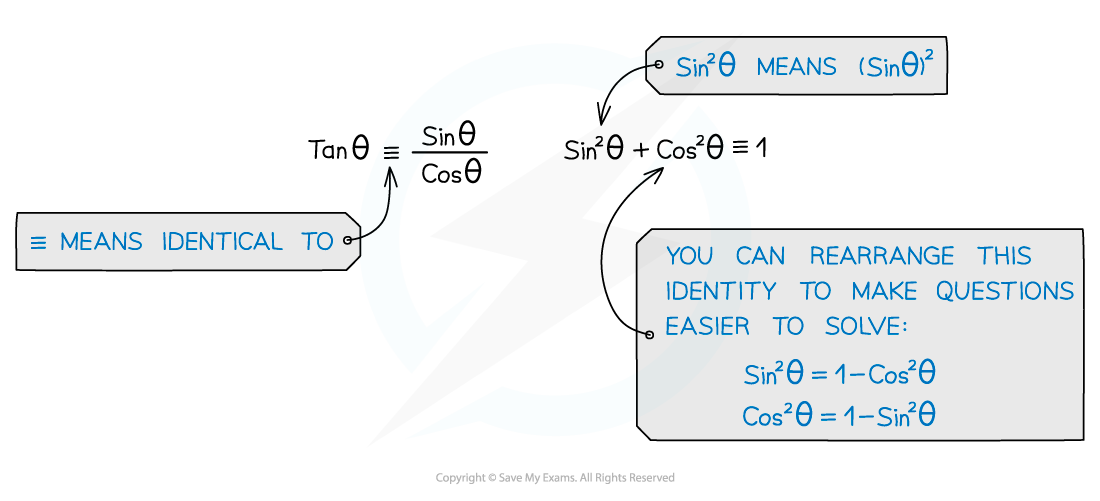
Trigonometry - Simple Identities Diagram 1, A Level & AS Level Pure Maths Revision Notes

Where do trigonometric identities come from?

  • Although you don’t need to know the proof for these identities it is important to understand where they come from

Trigonometry - Simple Identities Diagram 2a, A Level & AS Level Pure Maths Revision Notes
Trigonometry - Simple Identities Diagram 2b, A Level & AS Level Pure Maths Revision Notes

How do I use trigonometric identities?

Trigonometry - Simple Identities Diagram 3, A Level & AS Level Pure Maths Revision Notes

Examiner Tips and Tricks

  • You’ll need to remember these identities as they aren’t in the formula booklet.

  • If asked to show one thing is identical (≡) another look at what parts are missing –  for example, if tan x has gone it must have been substituted.

Worked Example

Trigonometry - Simple Identities Example Answer, A Level & AS Level Pure Maths Revision Notes
For teachers

Ready to test your students on this topic?

  • Create exam-aligned tests in minutes
  • Differentiate easily with tiered difficulty
  • Trusted for all assessment types
Explore Test Builder
Test Builder in a diagram showing questions being picked from different difficulties and topics, and being downloaded as a shareable format.
Test yourself
Previous:Exponential EquationsNext:Linear Trigonometric Equations
Lucy Kirkham

Author: Lucy Kirkham

Expertise: Head of Content Creation

Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.