Shortest Distances - Planes (Edexcel A Level Further Maths): Revision Note
Shortest Distance between a Point & a Plane
How do I find the shortest distance between a given point on a line and a plane?
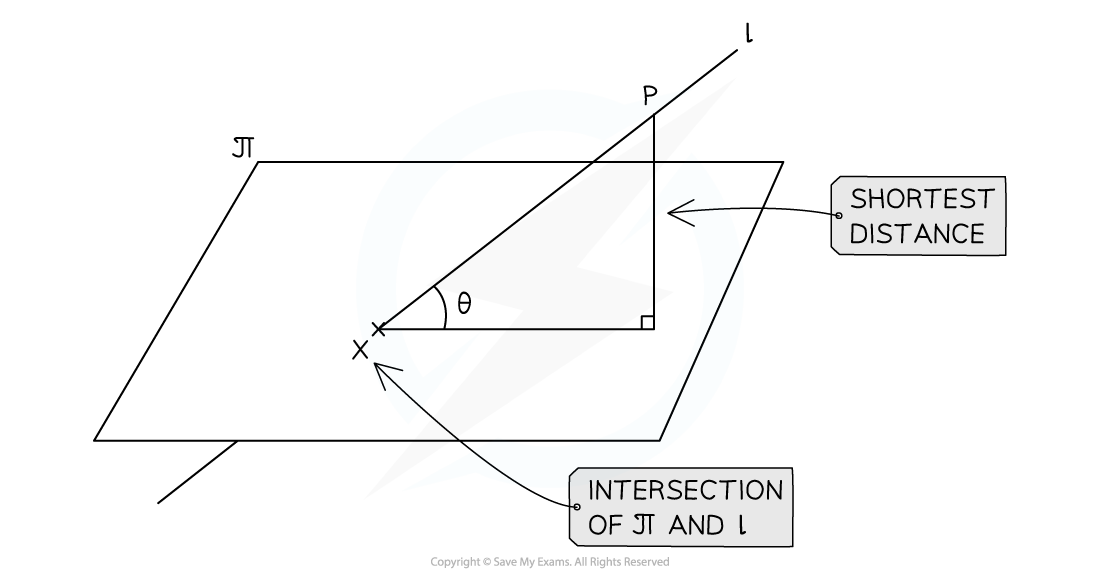
The shortest distance from any point on a line to a plane will always be the perpendicular distance from the point to the plane
Given a point, P, on the line
with equation
and a plane
with equation
STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on
This will have the position vector of the point, P, and the direction vector n
STEP 2: Find the coordinates of the point of intersection of this new line with
by substituting the equation of the line into the equation of the plane
STEP 3: Find the distance between the given point on the line and the point of intersection
This will be the shortest distance from the plane to the point
A question may provide the acute angle between the line and the plane
Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
Drawing a clear diagram will help
Worked Example
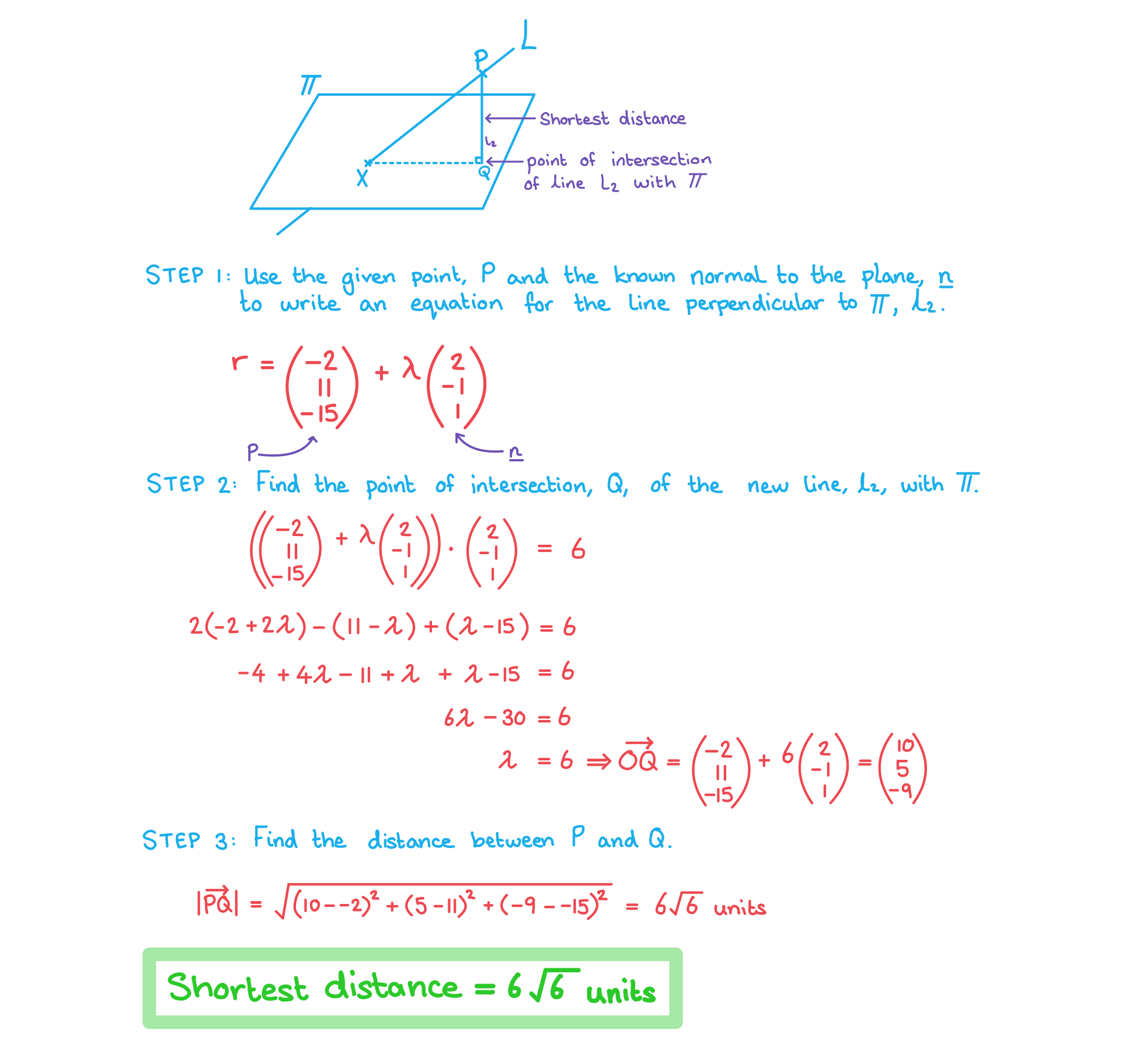
The plane has equation
.
The line has equation
.
The point lies on the line
.
Find the shortest distance between the point P and the plane .
Shortest Distance between a Line & a Plane
How do I find the shortest distance between a plane and a line parallel to the plane?
The shortest distance between a line and a plane that are parallel to each other will be the perpendicular distance from the line to the plane
Given a line
with equation
and a plane
parallel to
with equation
Where n is the normal vector to the plane
STEP 1: Find the equation of the line
perpendicular to
and
going through the point a in the form
STEP 2: Find the point of intersection of the line
and
STEP 3: Find the distance between the point of intersection and the point,

Shortest Distance between two Planes
How do I find the shortest distance between two parallel planes?
Two parallel planes will never intersect
The shortest distance between two parallel planes will be the perpendicular distance between them
Given a plane
with equation
and a plane
with equation
then the shortest distance between them can be found
STEP 1: The equation of the line perpendicular to both planes and through the point a can be written in the form r = a + sn
STEP 2: Substitute the equation of the line into
to find the coordinates of the point where the line meets
STEP 3: Find the distance between the two points of intersection of the line with the two planes
Consider the parallel planes defined by the equations:
,
.
a) Show that the two planes and
are parallel.

b) Find the shortest distance between the two planes and
.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
