The constant acceleration equation is used to model the horizontal displacement
at time t seconds of a projectile, where
and
are respectively the initial velocity and acceleration of the projectile in the horizontal direction.
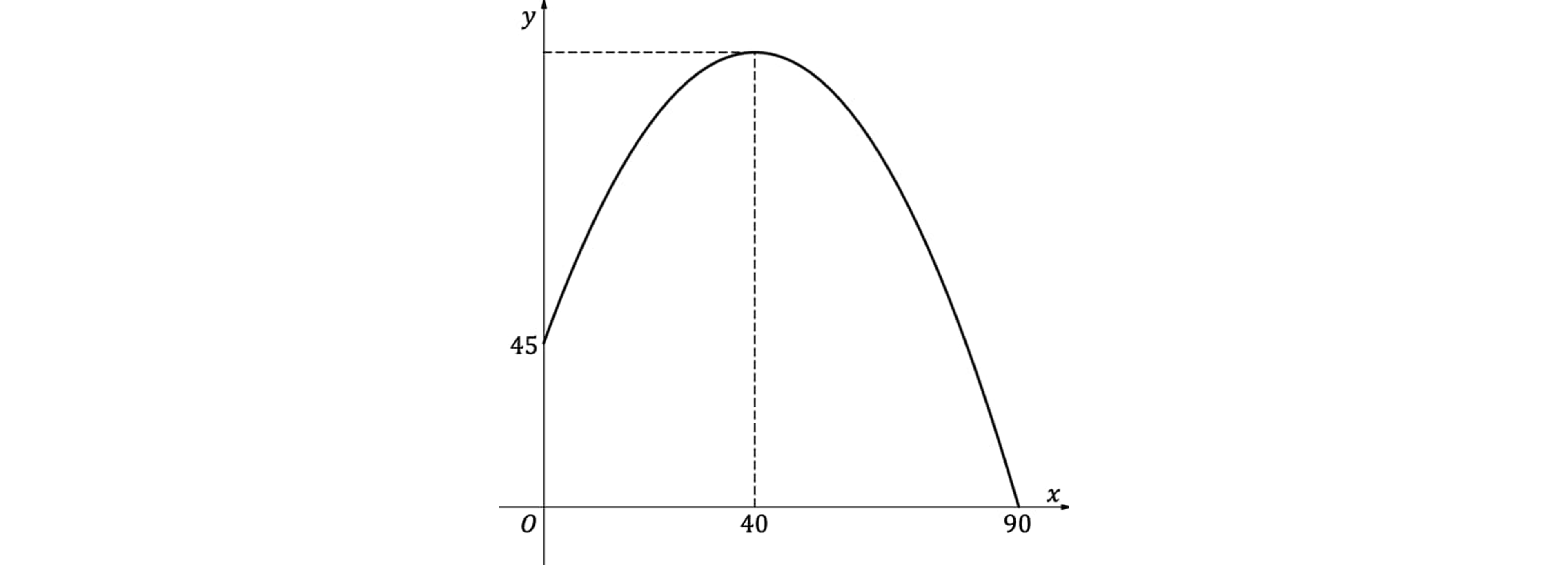
Show that , justifying any assumptions you make.
A projectile is projected horizontally from a set height with a velocity of .
It reaches the ground 5 seconds later.
Find the horizontal displacement of the projectile when it reaches the ground.
Taking the downward direction to be positive, use the constant acceleration equation to show that, to 3 significant figures, the height from which the projectile was projected is
.
Did this page help you?