Separation of Variables (OCR A Level Maths A): Revision Note
Exam code: H240
Did this video help you?
Separation of variables
What does it mean for a differential equation to be separable?

Many differential equations used in modelling have two variables involved (ie x and y)
If there is a product of functions in different variables, the differential equation is separable
ie dy/dx = f(x) × g(y)
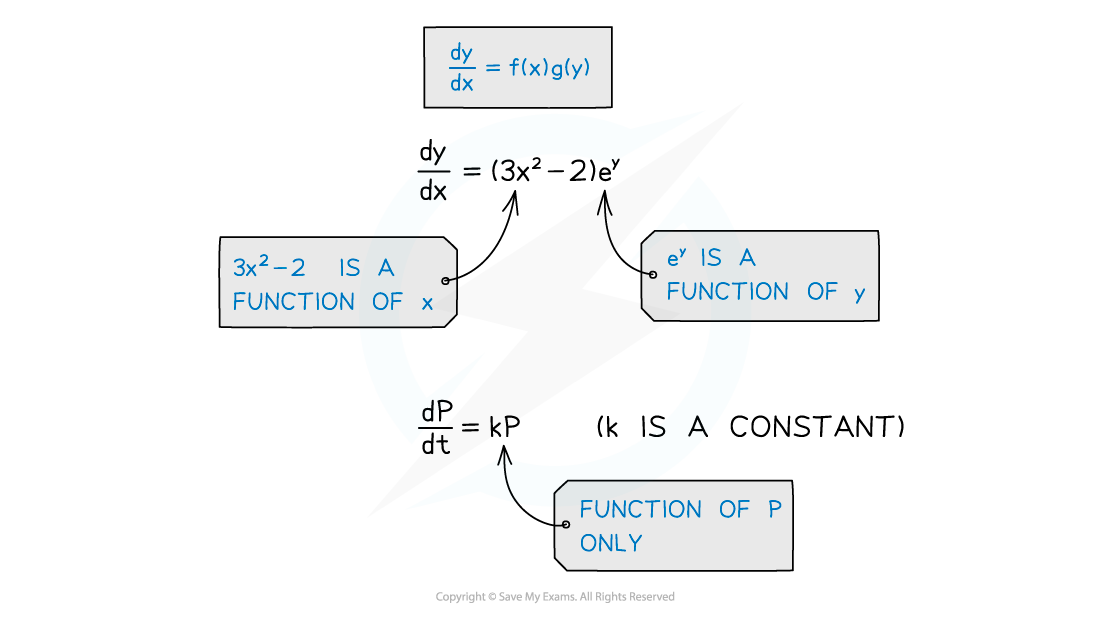
Differential equations of the form dy/dx= g(y) should be though t of as dy/dx= 1 × g(y)
where f(x) = 1
How do I solve a differential equation using separation of variables?
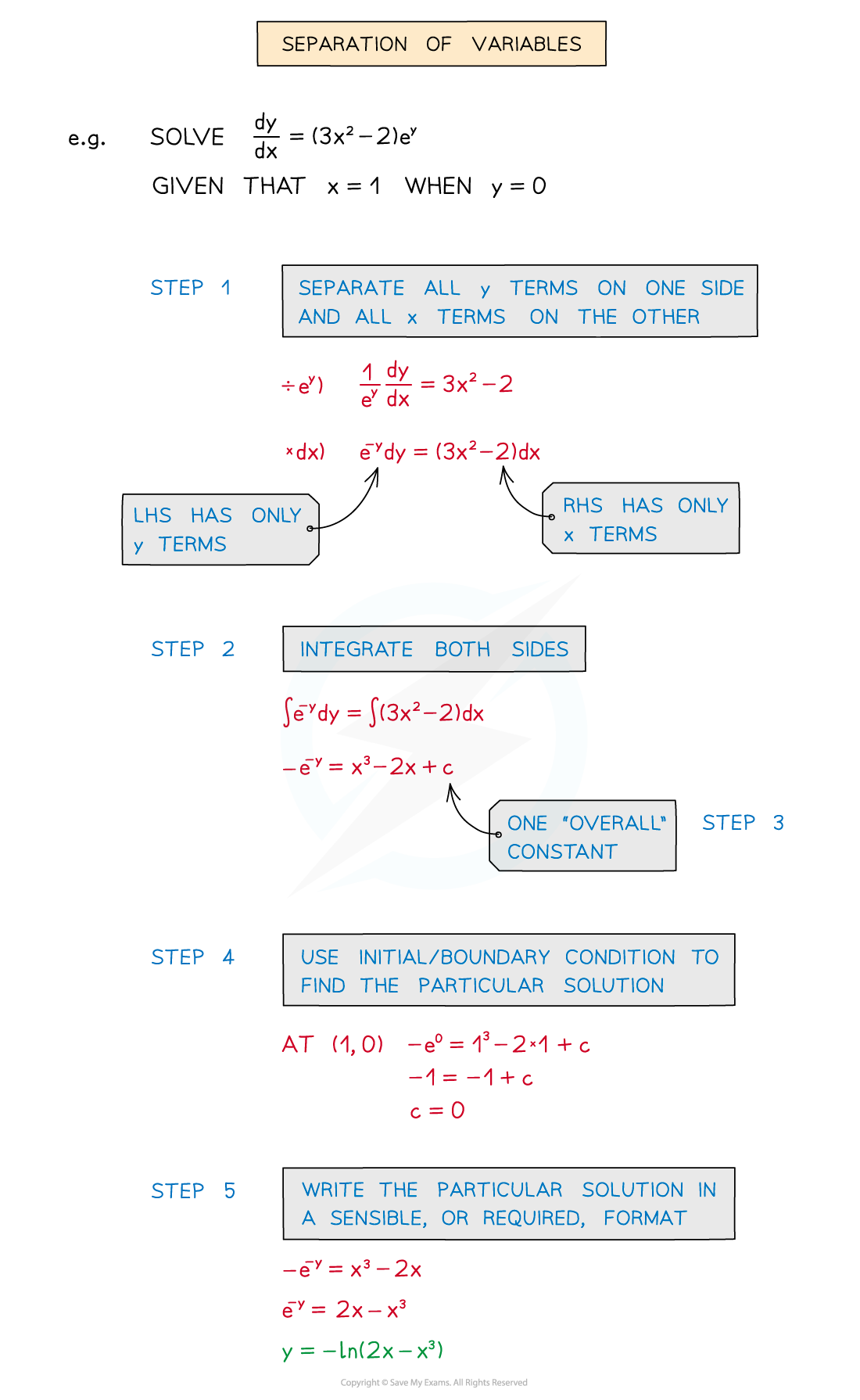
STEP 1: Separate all y terms on one side and all x terms on the other side
STEP 2: Integrate both sides
STEP 3: Include one “overall” constant of integration
STEP 4: Use the initial or boundary condition to find the particular solution
STEP 5: Write the particular solution in sensible, or required, format
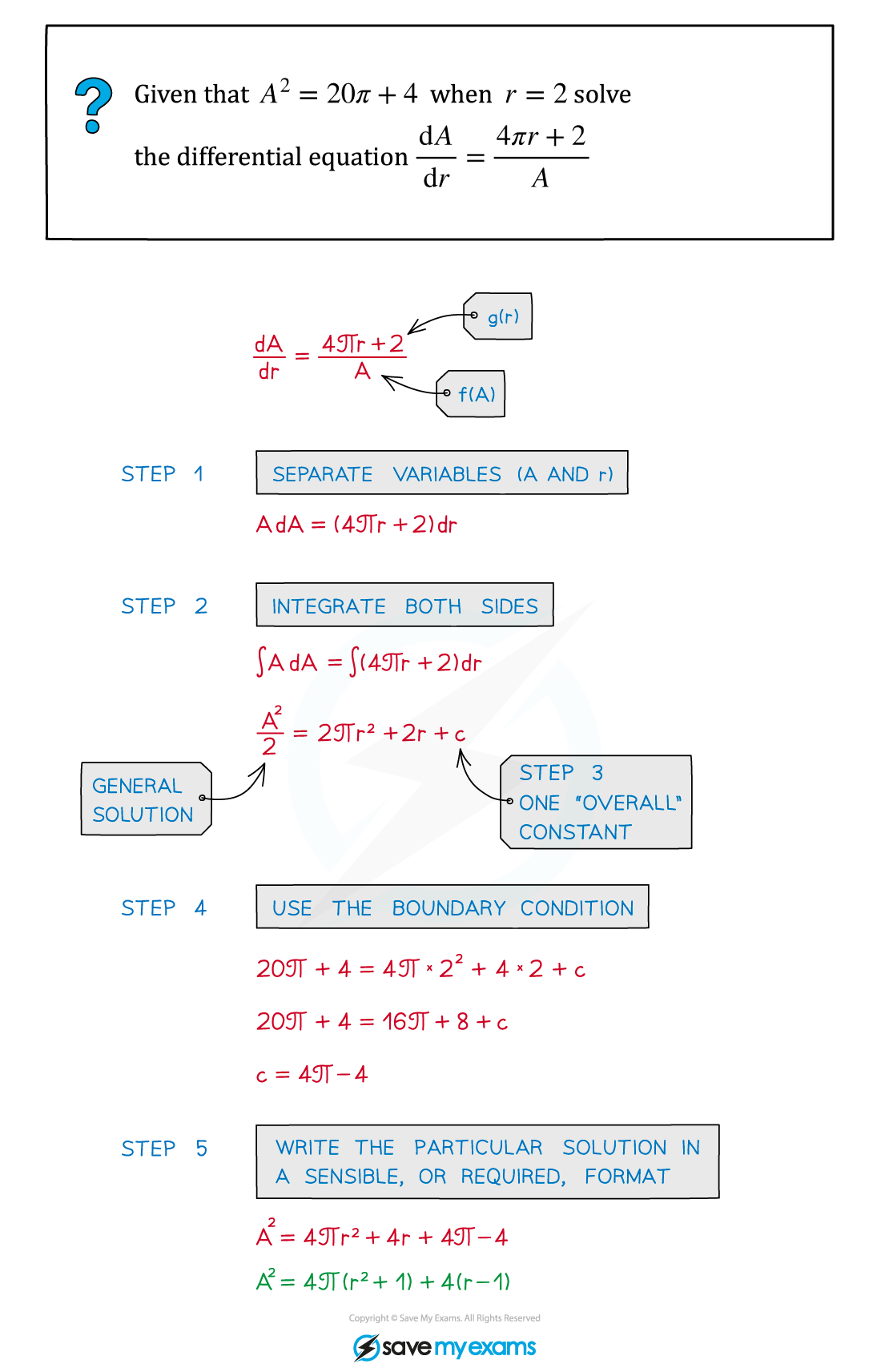
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?