Further Parametric Equations (Edexcel International A Level (IAL) Maths: Pure 4): Exam Questions

Find an expression for in terms of for the parametric equations:

Find an expression for in terms of t for the parametric equations

Verify that the graph of against y passes through the point (0, 1) and find the gradient at that point.

The graph defined by the parametric equations

x=5t-1 y = t≥ 0

is shown below.

The point where t = t₁ has coordinates (-1,0).

The point where t = t₂ has coordinates (4, 1).

(i) Show that the shaded area can be found using the integral

(ii) Hence find the shaded area.

A crane swings a wrecking ball along a two-dimensional path defined by the parametric equations

x = 8t -4 y=16t²-16t + 5 0 ≤ t ≤ 1

as shown in the diagram below.

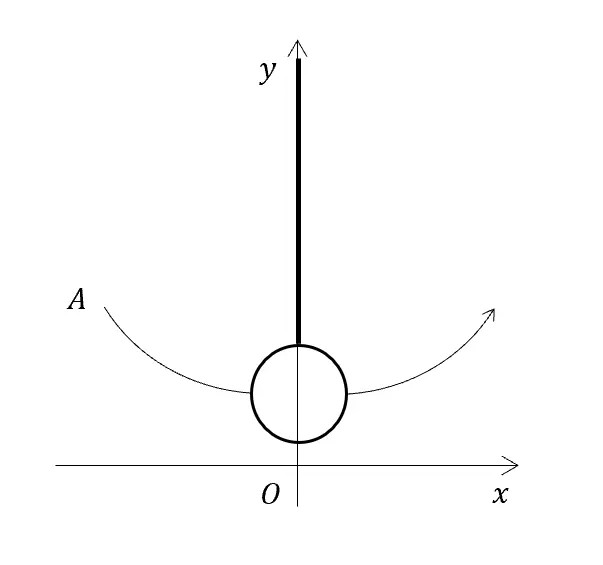
x and y are, respectively, the horizontal and vertical displacements in metres from the origin, 0, and t is the time in seconds. Point A indicates the initial position of the wrecking ball, at time t = 0.

Find a Cartesian equation of the curve in the form y = f(x), and state the domain of f(x).

Find the difference between the maximum and minimum heights of the wrecking ball during its motion.

The crane is positioned such that point A is 7 m horizontally from the wall the wrecking ball is to destroy.

Find the height at which the wrecking ball will strike the wall.

The graph of the curve C shown below is defined by the parametric equations

x = 2 cos 3 y = 5 sin 0 ≤ ≤ 2

Find an expression for in terms of .

(i) Show that the gradient of the tangent to C, at the point where , is .

(ii) Hence find the equation of the tangent to C at the point where .

The curve C has parametric equations

x = t>0

Find an expression, in terms of t, for

(i) Find the gradient of the tangent to C at the point where t =

(ii) Hence find the equation of the normal to C at the point where t =

The curve C has parametric equations

Show that at the point (0, 6), and find the value of at this point.

The tangent at the point (0, 6) is parallel to the normal at the point P.

Find the exact coordinates of point P

A curve C has parametric equations

The tangents to C at the points R and S meet at the point T, as shown in the diagram below.

Given that the x-coordinate of both points R and S is 5, find the area of the triangle RST.

A model car travels on a model track along the path of the curve shown in the diagram below. The curve is defined by the parametric equations

where and are, respectively, the horizontal and vertical displacements in metres from the origin , and is the time in seconds.

(i) Write down the coordinates of the starting position of the model car.

(ii) Indicate on the graph in which direction the model car travels.

(iii) How many laps of the track will the model car complete?

Find the times during the first lap at which the model car is at a “crossroads” – indicated by points and on the graph.

Find the speed of the model car at the start of the final lap.

The diagram below shows the curve with parametric equations

Find the coordinates of the points where intersects the -axis, and determine the corresponding values of .

The region shown in the diagram is bounded by and the -axis. Region is rotated through radians about the -axis to form a solid of revolution.

(i) Show that the volume of the solid of revolution is given by the integral

(ii) Hence find the exact volume of the solid generated.

The shaded area in the diagram below is bounded on three of its sides by the -axis, the -axis, and the line . On the remaining side, the boundary is defined by the parametric equations

Show that the shaded area is not a trapezium.

In your work, you may use without proof the result