Regression Lines (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note
Exam code: 1350
Calculating & Using Regression Lines
How do I draw a line of best fit?
If strong linear correlation exists on a scatter diagram, then a line of best fit can be drawn
A line of best fit can be drawn by eye following the trend of the data points
For a linear correlation it is a straight line
It must go through the mean point
There should be an approximately equal number of points above and below the line
What is a regression line?
A line of best fit drawn by eye can be inaccurate, however the equation of an accurate line of best fit can be calculated
This is called the regression line
The least squares regression line is the line of best fit that minimises the sum of the squares of the gap between the line and each data value
If the regression line is calculated by looking at the vertical distances it is called the regression line of y on x
If the regression line is calculated by looking at the horizontal distances it is called the regression line of x on y
The regression line of x on y is rarely used and is not in this course
The regression line of y on x is written in the form
is the gradient of the line and represents the change in
for each individual unit change in
is the
-intercept and shows the value of
for which
is zero
The point
will lie on the regression line
You may be expected to:
work out the equation of the regression line from raw data using your calculator
draw a line of regression onto a scatter diagram
interpret or use a regression line to predict values
define
and
in the context of the question
How do I find the line of regression?
Most calculators will be able to calculate the equation for the line of regression when you input raw data
Select the statistics function on your calculator
Input the
and
values from the given data set
Use the option to generate the regression line or the line
The calculated values for
and
are likely to be given to a number of decimal places
Round to an appropriate degree of accuracy when writing them into the equation, e.g. 13 s.f.
Examiner Tips and Tricks
Make sure you know how to find the line of regression on your calculator as every calculator is different!
How do I draw the regression line from the equation?
Drawing a regression line is done in the same way as drawing a straight line graph
Plot the point
Substitute values for
into the equation to find values of
Connect two or more found points with a straight line
The equation of the regression line can be used to decide what type of correlation there is if there is no scatter diagram
If a is positive then the data set has positive correlation
If a is negative then the data set has negative correlation
Examiner Tips and Tricks
Remember that the value of is the gradient of the regression line, it is not the strength of the correlation.
Worked Example
The table of values below shows the number of Save My Exams question packs completed by a group of students, , and the percentage score they received in their Statistics exam,
.
No. SME question packs completed | Percentage scored on exam | ||
|---|---|---|---|
10 | 0 | ||
31 | 32 | ||
12 | 38 | ||
51 | 100 | ||
29.5 | 65 | ||
24.5 | 35 | ||
39 | 59 | ||
50 | 92 | ||
30.5 | 76 | ||
60 | 78 |
(a) Find the equation of the regression line of on
in the form
Input the values into your calculator and calculate the line of regression
The scatter graph of the results is shown below.
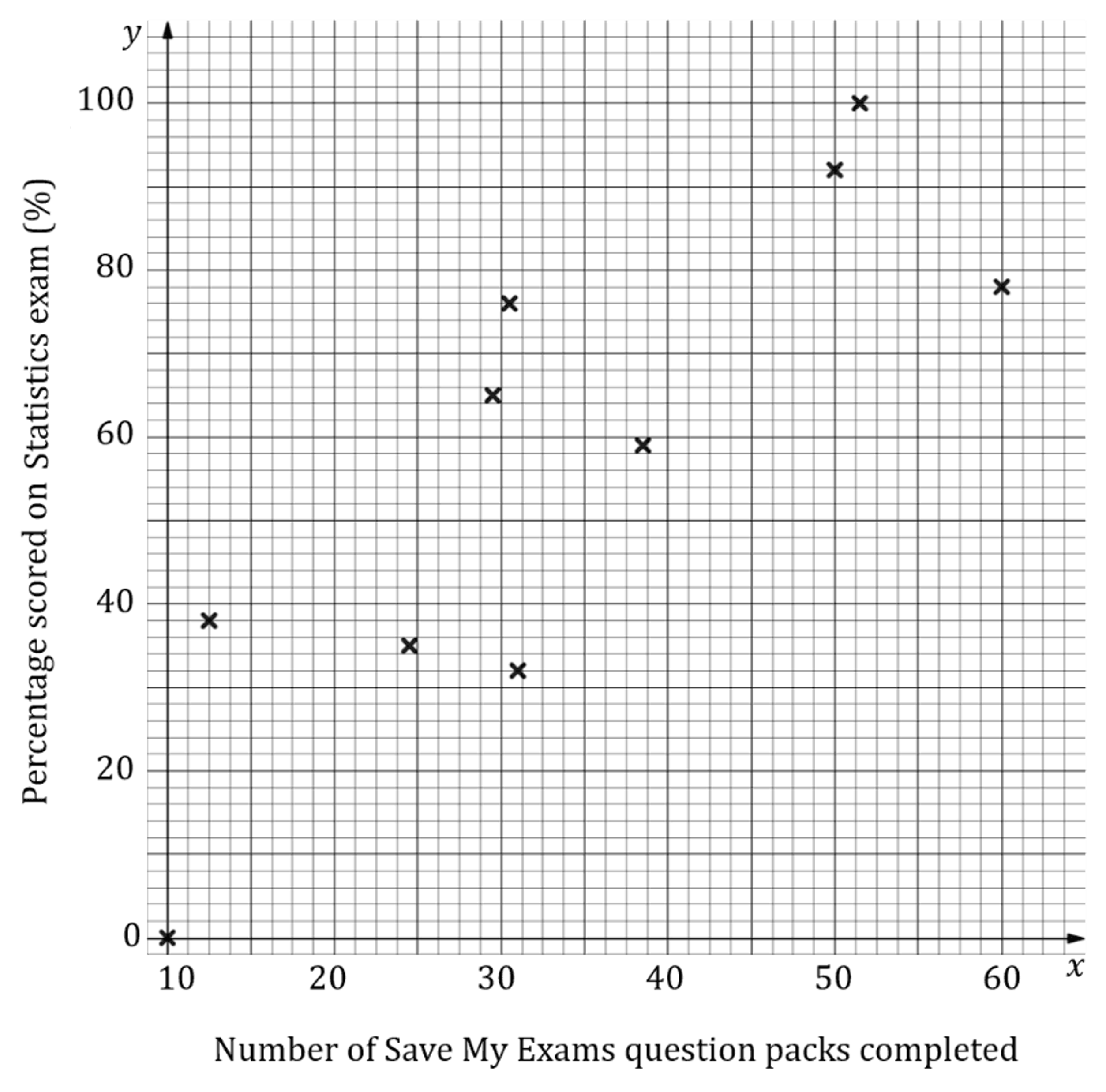
(b) Draw the regression line onto the scatter diagram.
Substitute values into the equation
When ,
When ,
Plot points on the graphs and draw a straight line through them
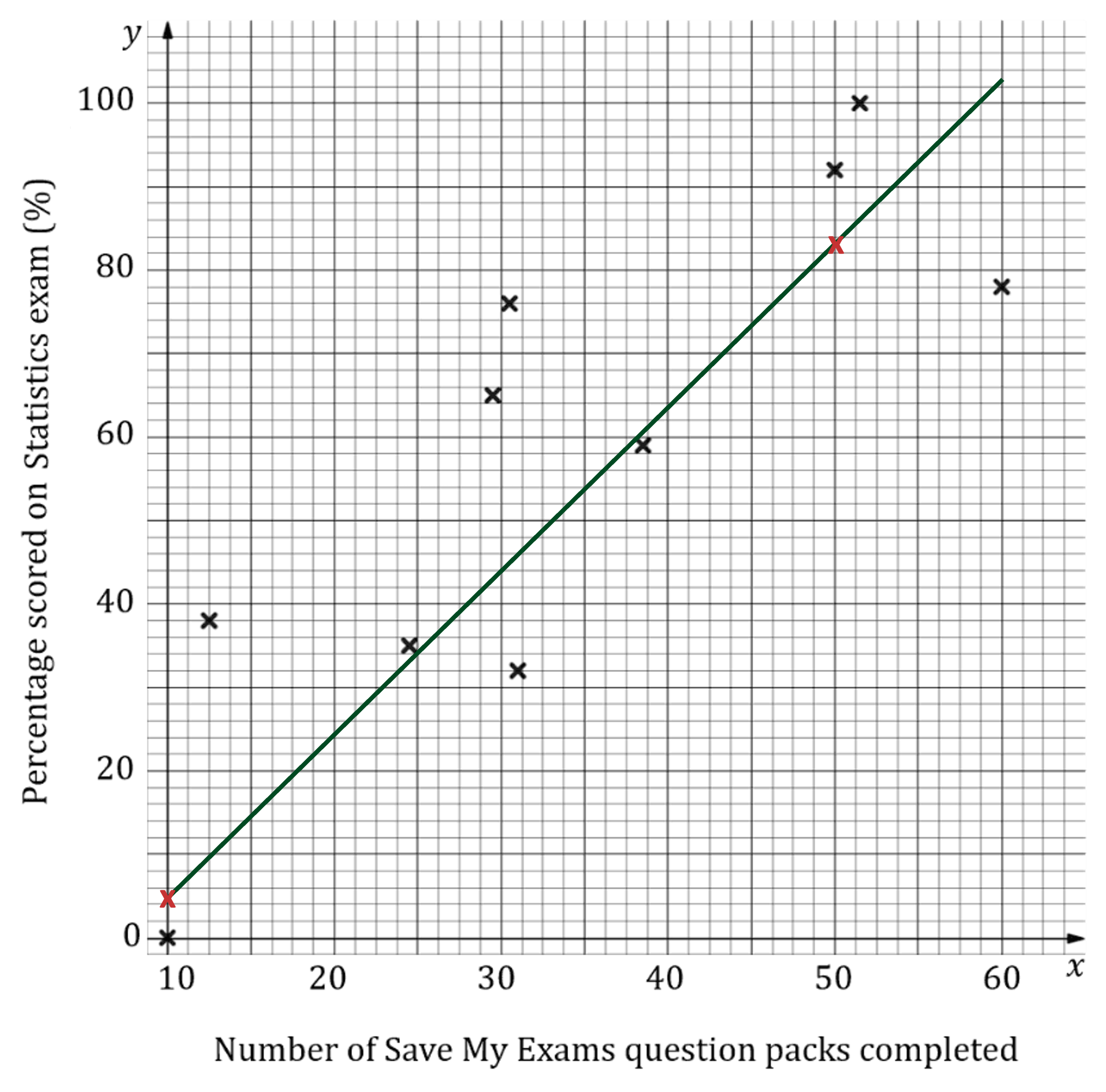
(c) Explain, in context, the meaning of the values of and
.
is the
-intercept, it is the value for
when
is the score (4.66%) that a person would expect to get in their Statistics exam if they competed no SME question packs
is the gradient of the line, it is the change in
over the change in
is the increase in percentage score (1.57%) in their Statistics exam for every completed SME question pack
Interpolation & Extrapolation
The equation of the regression line can also be used to predict the value of a dependent variable (y) from an independent variable (x)
The equation should only be used to make predictions for y
Using a y on x line to predict x is not always reliable
Predictions should only be made for values of the dependent variable that are within the range of the given data
Making a prediction within the range of the given data is called interpolation
Making a prediction outside of the range of the given data is called extrapolation and is much less reliable
The prediction will be more reliable if the number of data values in the original sample set is bigger
Worked Example
The table below shows the daily mean pressure, (hPa), and daily total sunshine,
(hrs), in Camborne for a random sample of 12 days in 2015.
1007 | 1023 | 1011 | 1022 | 1011 | 1019 | 1017 | 1016 | 1022 | 997 | 1030 | 1023 | |
0 | 6.3 | 2.4 | 6.2 | 1.7 | 8.4 | 1.9 | 6.7 | 7.7 | 2.3 | 10.3 | 4.1 |
The equation of the regression line of on
is
(a) Give an interpretation of the value of the gradient of the regression line.
For unit on the -axis there is a 0.271 increase in the
-axis
0.271 hour increase in sunshine for every 1 hPa pressure increase
(b) Use the regression line equation to find an estimate for the daily total sunshine in hours when the daily mean pressure is 1003.
Substitute into the equation of the regression line
hours
(c) Explain why the regression line given should not be used to estimate the daily total hours of sunshine when the daily mean pressure is 1035.
The value of the pressure is outside of the sample range (extrapolating), so result would be less likely to be accurate
is outside the range of the of values for
,

Unlock more, it's free!
Did this page help you?