Break-Even Analysis (AQA A Level Business): Revision Note

The value of break-even analysis

• Break Even analysis is a financial tool used to determine the point at which the business revenue equals its expenses, resulting in neither profit nor loss

• It helps businesses understand the minimum level of sales or output they need to achieve in order to cover all costs

  • This helps managers make informed decisions about pricing and production volumes

• It is particularly useful for communicating with stakeholders, including investors or lenders

  • It demonstrates the financial viability of the business and gives an insight into potential returns on investment

Revenue and costs

• Break Even analysis takes into account three main components

The components of break-even analysis

Sales revenue

• Sales Revenue is the value of the units sold by a business over a period of time

  • E.g the revenue earned by Apple Music from sales of music downloads 

  • Sales revenue is a key business performance measure and must be calculated to identify profit

  • Sales revenue is calculated using the formula

  
   

  • Sales revenue increases as the sales volume increases

Costs

• In preparing goods and services for sale, businesses incur a range of costs

  • Some examples of these these costs include purchasing raw materials, paying staff salaries and wages, and paying utility bills such as electricity  

• These costs can be broken into different categories

  • Fixed costs (FC) are costs that do not change as the level of output changes

    • These have to be paid whether the output is zero or 5000 

  • Variable costs (VC) are costs that vary directly with the output

    • These increase as output increases & vice versa

  • Total costs (TC) are the sum of the fixed + variable costs 

Fixed costs (FC)

• The firm has to pay its fixed costs which do not change, irrespective if the output is 0 or 100,000 units

• The fixed costs for this firm are $4,000

Variable costs (VC)

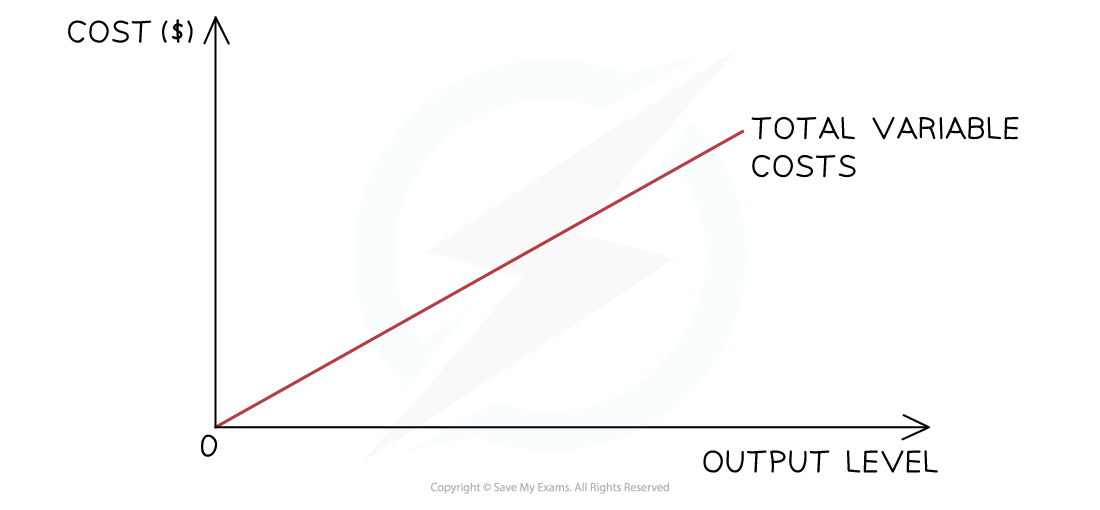
• The variable costs initially rise proportionally with output, as shown in the diagram

• At some point, the firm will benefit from a purchasing economy of scale and the rise will no longer be proportional

Total costs (TC)

• The total cost is the sum of the variable and fixed costs at each level of output

• Total costs cannot be 0, as all firms have some level of fixed costs

Constructing and interpreting break-even charts

• A break-even chart is a visual representation of the break-even point and is used to identify the following:

  • Fixed costs, total costs and revenue over a range of output

  • The break even point - where total costs are equal to revenue

  • Profit or loss made at each level of output

  • The margin of safety

Diagram: break even chart

Diagram analysis 

• Fixed costs do not change as output increases

  • A2B's fixed costs are £8,000 and these do not change whether the business produces 0 units or 500 units 

• Total costs are made up of fixed and variable costs

  • At 0 units of output, they are made up exclusively of fixed costs

  • At 500 units the total variable costs equate to £11,800

  • This line slopes upwards because total variable costs increase as output increases 

• The revenue line also slopes upwards

  • At 0 units of output, the revenue is £0

  • At 500 units the total revenue equates to £11,800

  • Revenue will increase with the output

  • The line will slope more steeply than the total costs and will cross the total costs line at some point 

• The break even point is the point at which the total costs and the revenue lines cross each other

  • The break even level of output for A2B is 324 units

• The margin of safety can be identified as the difference on the x-axis between the actual level of output (in this case 450 units) and the break even point (324 units)
  

• The profit made at a specific level of output can be identified as the space between the revenue and total costs lines

  • In this instance the profit made at 450 units of output is £14,400 - £11,250 = £3,150

Illustrating changes to price, output and costs on the break-even chart

• Changing any of the variables of break-even (selling price, variable cost per unit or total fixed costs) changes the break-even point and level of profit it can expect to achieve

Changes in variables and the break-even point

Increased selling price

• An increase in the selling price increases revenue at each level of output from R₁ to R₂

• The break-even point falls from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is increased

Decreased selling price

• A decrease in the selling price reduces revenue at each level of output from R₁ to R₂

• The break-even point rises from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is decreased

Increased variable costs

• An increase in variable costs increases total costs at each level of output from TC₁ to TC₂

• The break-even point increases from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is decreased

Decreased variable costs

• A decrease in variable costs decreases total costs at each level of output from TC₁ to TC₂

• The break-even point falls from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is increased

Increased fixed costs

• An increase in fixed costs increases total costs at each level of output from TC₁ to TC₂

• The break-even point increases from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is decreased

Decreased fixed costs

• A decrease in fixed costs reduces total costs at each level of output from TC₁ to TC₂

• The break-even point falls from BEP₁ to BEP₂

• Profit on each unit of output greater than the break-even point is increased

The benefits and limitations of break-even analysis

Benefits of break-even analysis

Limitations of break-even analysis

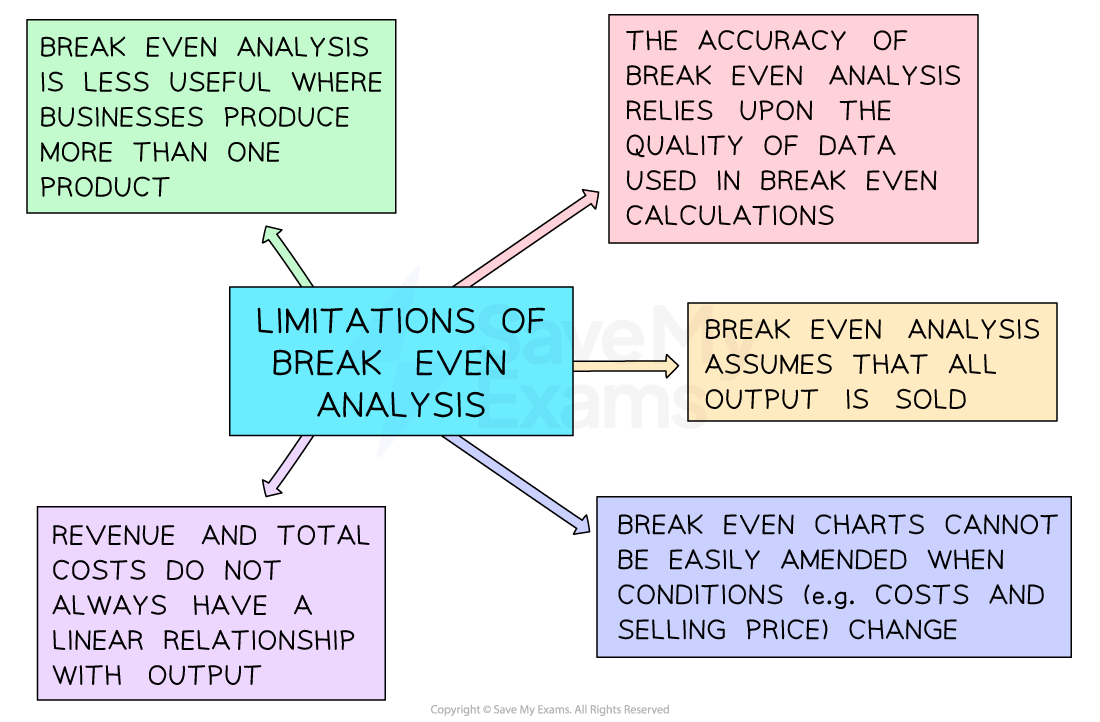
Using break-even analysis to inform decisions