Quadratic Inequalities (Edexcel A Level Maths) : Revision Note

Quadratic Inequalities

Quadratic inequalities

• Similar to quadratic equations quadratic inequalities just mean there is a range of values that satisfy the solution

• Sketching a quadratic graph is essential

Can involve the discriminant or applications in mechanics and statistic

How do I solve quadratic inequalities?

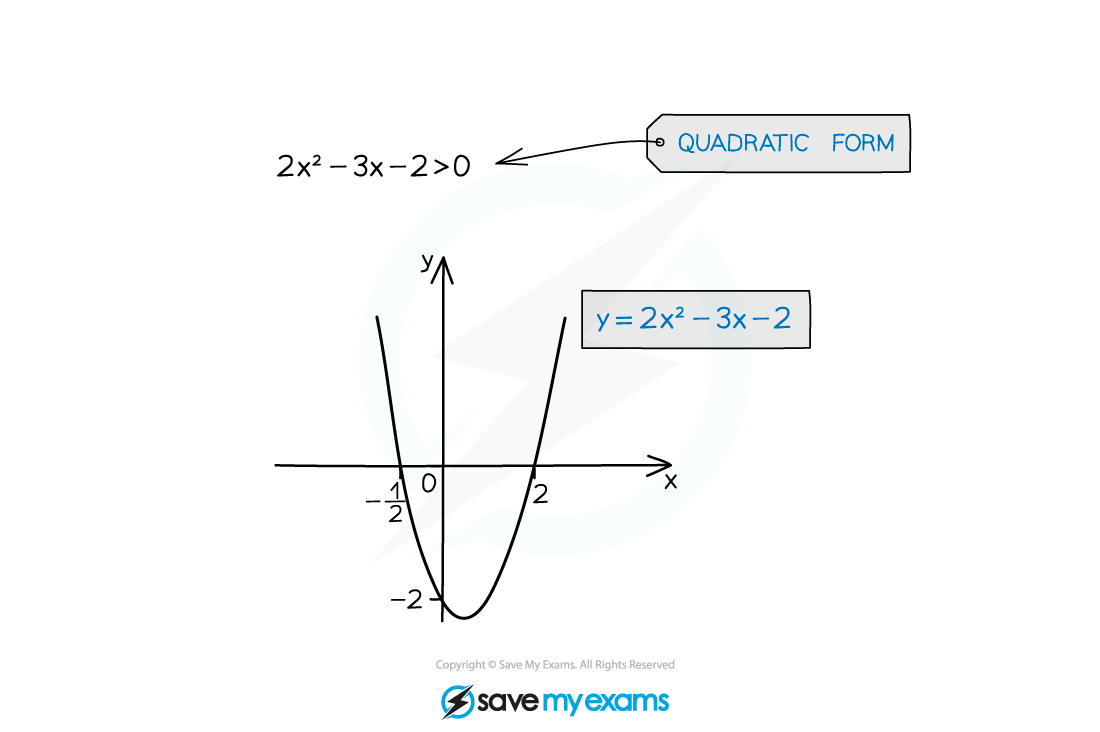
• STEP 1: Rearrange the inequality into quadratic form with a positive squared term

  • ax² + bx + c > 0 (>, <, ≤ or ≥)

• STEP 2: Find the roots of the quadratic equation

  • Solve ax² + bx + c = 0 to get x₁ and x₂ where x₁ < x₂

• STEP 3: Sketch a graph of the quadratic and label the roots

  • As the squared term is positive it will be "U" shaped

• STEP 4: Identify the region that satisfies the inequality

  • For ax² + bx + c > 0 you want the region above the x-axis

    • The solution is x < x₁ or x > x₂ 

  • For ax² + bx + c < 0 you want the region below the x-axis

    • The solution is x > x₁ and x < x₂  

    • This is more commonly written as x₁ < x < x₂

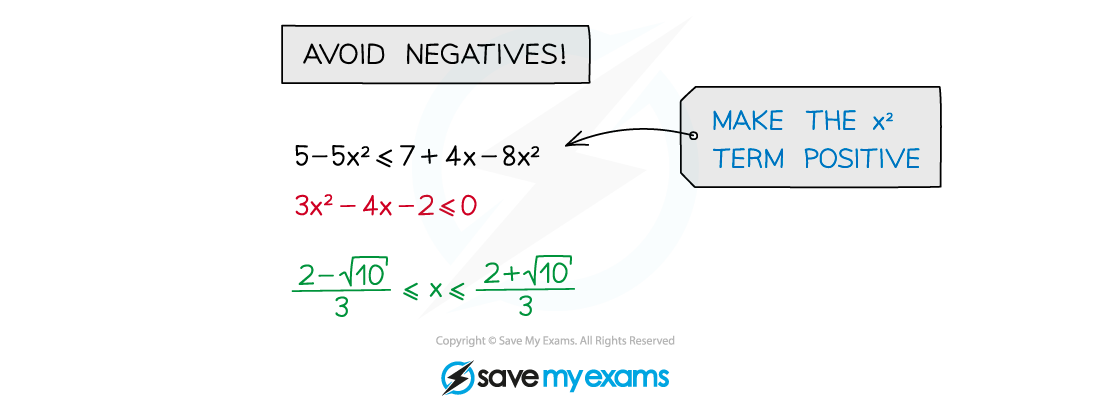
• avoid multiplying or dividing by a negative number

  if unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc

  • avoid multiplying or dividing by a variable (x) that could be negative

    (multiplying or dividing by x² guarantees positivity (unless x could be 0) but this can create extra, invalid solutions)

  • do rearrange to make the x² term positiveBe careful:

Solving quadratic inequalities on a calculator

• Be aware of unconventional ways calculators can display an answer

  eg        8 > x > 2 rather than 2 < x < 8