Newton-Raphson Method (Edexcel A Level Maths): Revision Note
Exam code: 9MA0
Did this video help you?
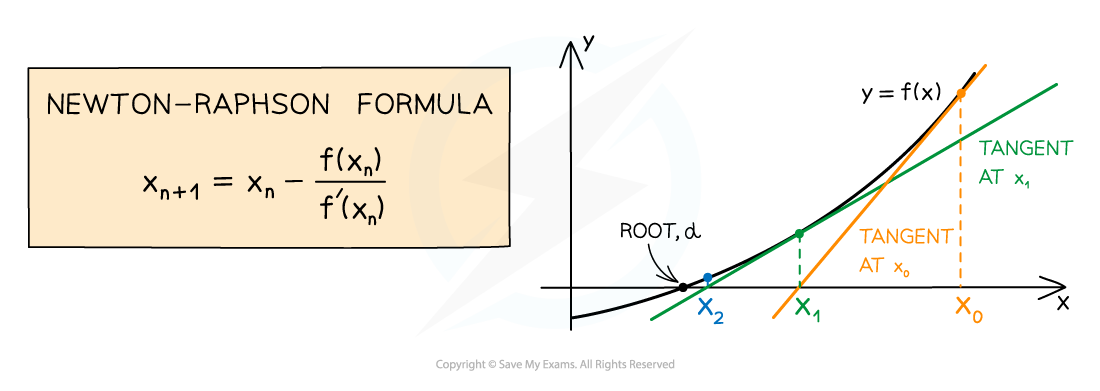
Newton-Raphson method
What is the Newton-Raphson method?
The Newton-Raphson method finds roots of equations in the form f(x) = 0
It can be used to find approximate solutions when an equation cannot be solved using the usual analytical methods
It works by finding the x-intercept of tangents to f(x) to get closer and closer to a root
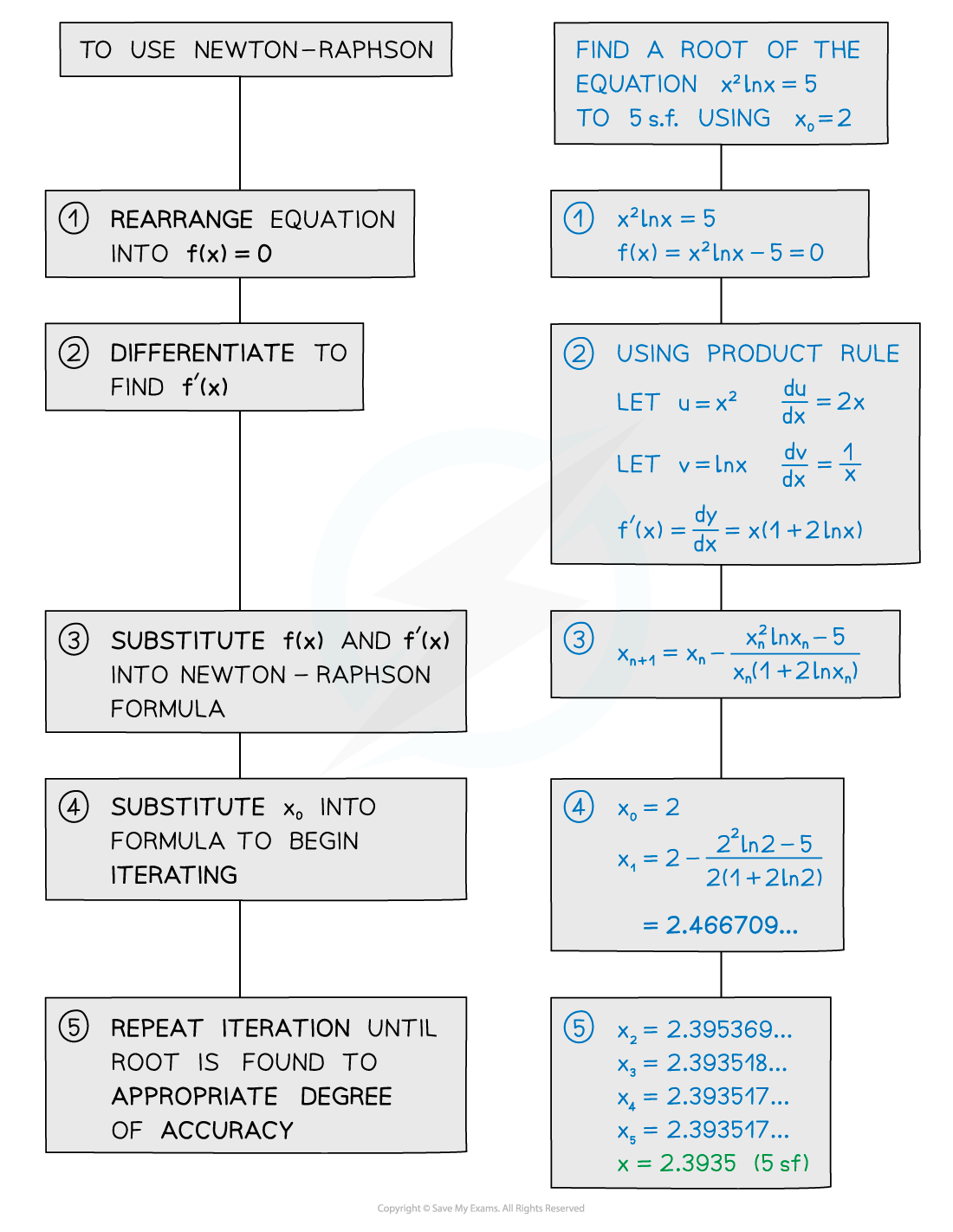
How do I use the Newton-Raphson method?
The formula for Newton-Raphson uses the same xn + 1 = f(xn) notation as used in iteration and other recurrence relations
After using differentiation to find f’(x) the formula uses iteration to come to an ever more accurate solution
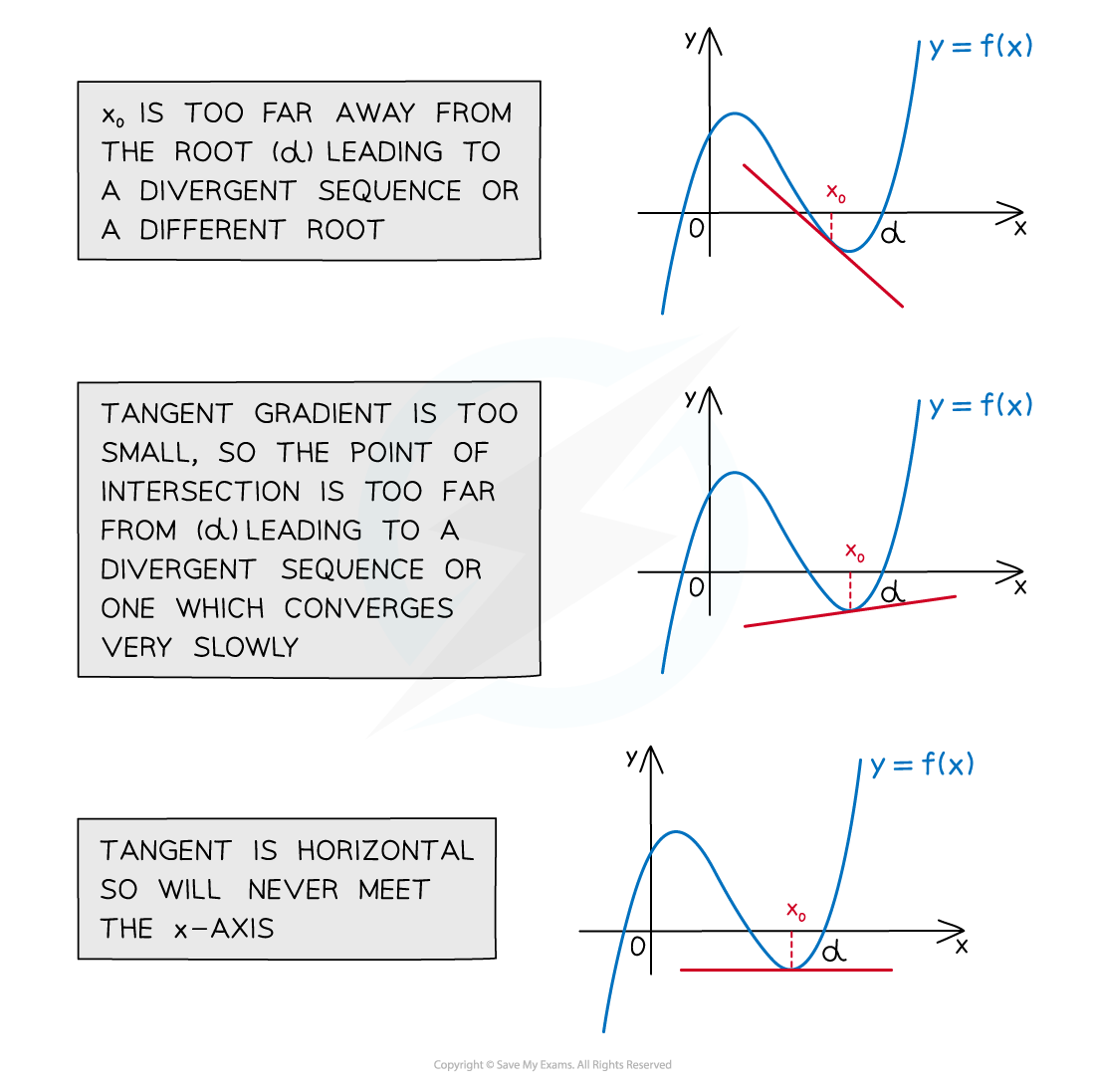
Can the Newton-Raphson method fail?
The Newton-Raphson method can fail when:
the starting value x0 is too far away from the root leading to a divergent sequence or a different root
the tangent gradient is too small, where f’(x) close to 0 leading to a divergent sequence or one which converges very slowly
the tangent is horizontal, where f’(x) = 0 so the tangent will never meet the x‑axis
the equation cannot be differentiated (or is awkward and time-consuming to do)
Examiner Tips and Tricks
The formula for the Newton-Raphson method is given in the formula booklet.
Use ANS button on your calculator to calculate repeated iterations.
Keep track of your iterations using x2, x3… notation.
Newton-Raphson questions may be part of bigger numerical methods questions.
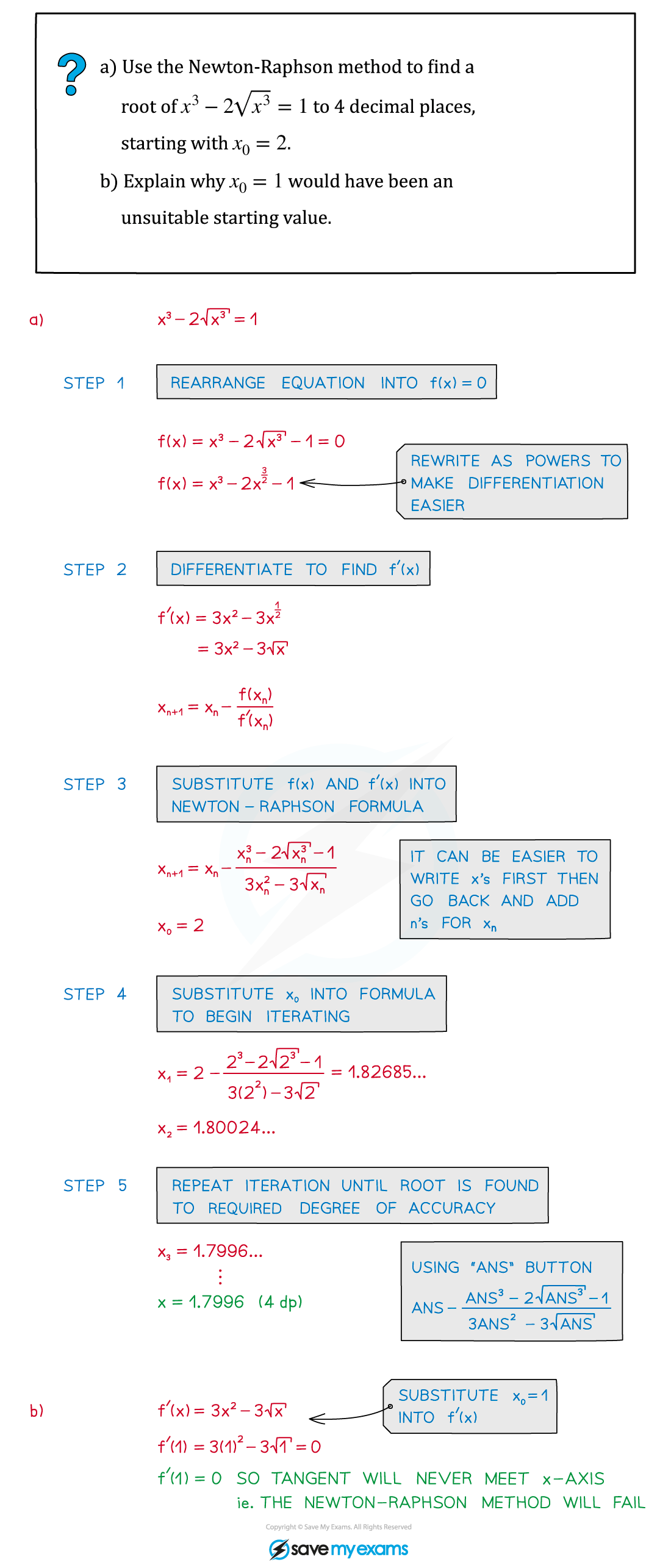
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?