Sample Mean Distribution (OCR A Level Maths A): Revision Note
Exam code: H240
Did this video help you?
Sample mean distribution
What is the distribution of the sample means?
For any given population it can often be difficult or impractical to find the true value of the population mean, µ
The population could be too large to collect data using a census or
Collecting the data could compromise the individual data values and therefore taking a census could destroy the population
Instead, the population mean can be estimated by taking the mean from a sample from within the population
If a sample of size n is taken from a population, X, and the mean of the sample,
is calculated then the distribution of the sample means,
, is the distribution of all values that the sample mean could take
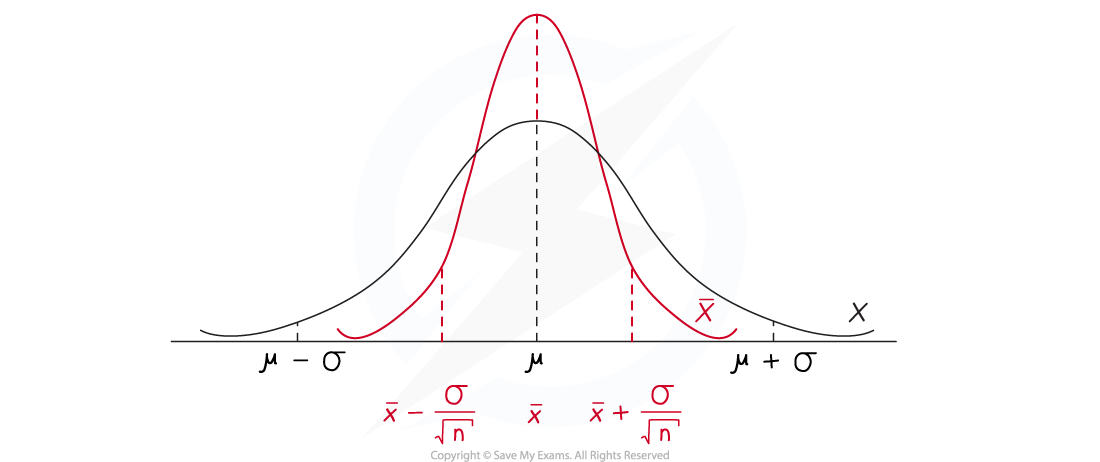
If the population, X, has a normal distribution with mean, µ , and variance, σ2 , then the mean expected value of the distribution of the sample means,
would still be µ but the variance would be reduced
Taking a mean of a sample will reduce the effect of any extreme values
The greater the sample size, the less varied the distribution of the sample means would be
The distribution of the means of the samples of size taken from the population, will have a normal distribution with:
Mean,
= µ
Variance
Standard deviation
For a random variable
the distribution of the sample mean would be
The standard deviation of the distribution of the sample means depends on the sample size, n
It is inversely proportional to the square root of the sample size
This means that the greater the sample size, the smaller the value of the standard deviation and the narrower the distribution of the sample means
Worked Example
A random sample of 10 observations is taken from the population of the random variable and the sample mean is calculated as
. Write down the distribution of the sample mean,
.
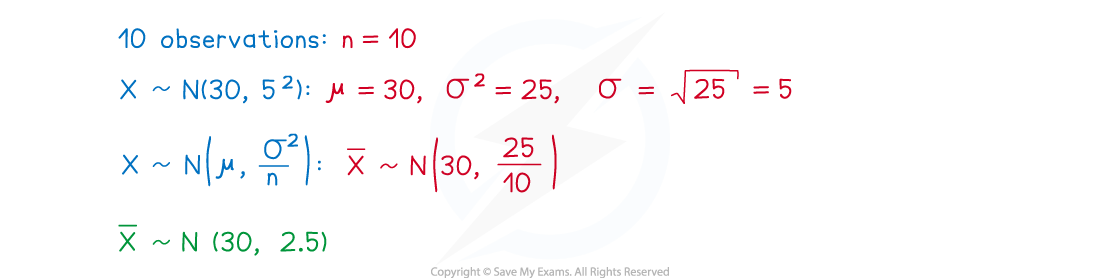
Examiner Tips and Tricks
Look carefully at the distribution given to determine whether the variance or the standard deviation has been given.

Unlock more, it's free!
Did this page help you?