Points of Intersection (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on 2 May 2024

Graphical Solutions

How do I use graphs to solve linear simultaneous equations?

The point of intersection of the two graphs is the solution to the pair of simultaneous equations
Plot both equations on the same set of axes using straight line graphs $y = m x + c$
Find where the lines intersect (cross)
- The $x$ and $y$ solutions to the simultaneous equations are the $x$ and $y$ coordinates of the point of intersection
For example:
- To solve $2 x - y = 3$ and $3 x + y = 7$ simultaneously, first plot them both on the same graph as shown below
- Find the point of intersection: (2, 1)
- The solution is therefore $x = 2$ and $y = 1$

Points of intersection of 2x-y=3 and 3x+y=7

How do I use graphs to solve simultaneous equations where one is a quadratic?

Plot both functions on the same graph, and find their points of intersection
For example:
- To solve $y = x^{2} + 4 x - 12$ and $y = 1$ simultaneously, first plot them both on the same graph as shown below
  - Find the points of intersection: (-6.1, 1) and (2.1, 1) to 1 decimal place
    - Solutions using graphs will often only be approximate
  - The solutions are therefore approximately $x = - 6.1$ , $y = 1$ and $x = 2.1$ , $y = 1$
    - There are two pairs of $x$ , $y$ solutions as there are two points of intersection
    - To find the exact solutions, you could use algebra instead

Points of intersection of y = x^2 + 4x - 12 and y=1

How do I use graphs to solve other equations?

The solution to a pair of equations is their point of intersection
Solutions of $f (x) = 0$ are where the graph of $y = f (x)$ crosses the $x$ -axis
If asked to use the graph of $y = f (x)$ to solve a different equation
- Rearrange the equation to be solved into $f (x) = g (x)$ , where $g (x)$ is a different equation and both $f (x)$ and $g (x)$ can be drawn
- The solutions are the $x$ -coordinates of where $f (x)$ and $g (x)$ intersect
For example:
- If given the curve for $y = x^{3} + 2 x^{2} + 1$ and asked to solve $x^{3} + 2 x^{2} - x - 1 = 0$ then:
  - Rearrange $x^{3} + 2 x^{2} - x - 1 = 0$ to $x^{3} + 2 x^{2} + 1 = x + 2$
  - Draw the line $y = x + 2$ on the curve $x^{3} + 2 x^{2} + 1$
  - Read the $x$ -values of where the line and the curve cross
    In this case there would be 3 solutions
    Approximately $x = - 2.2$ , $x = - 0.6$ and $x = 0.8$

Points of intersection of y=x^3 + 2x^2 + 1 and y=x+2

Examiner Tips and Tricks

When solving a pair of linear simultaneous equations, remember to give an $x$ and a $y$ value for your final answer
Questions may use other variables, e.g. $h$ and $t$ to model height and time
- Make sure you are certain which variable is measured on which axis

Worked Example

Two electricians, Paul and Claire, charge an hourly rate and a call-out fee (the price to travel to a job) to their customers.

Paul charges £85 per hour, with a £10 call-out fee.

Claire charges £54 per hour, with a £50 call-out fee.

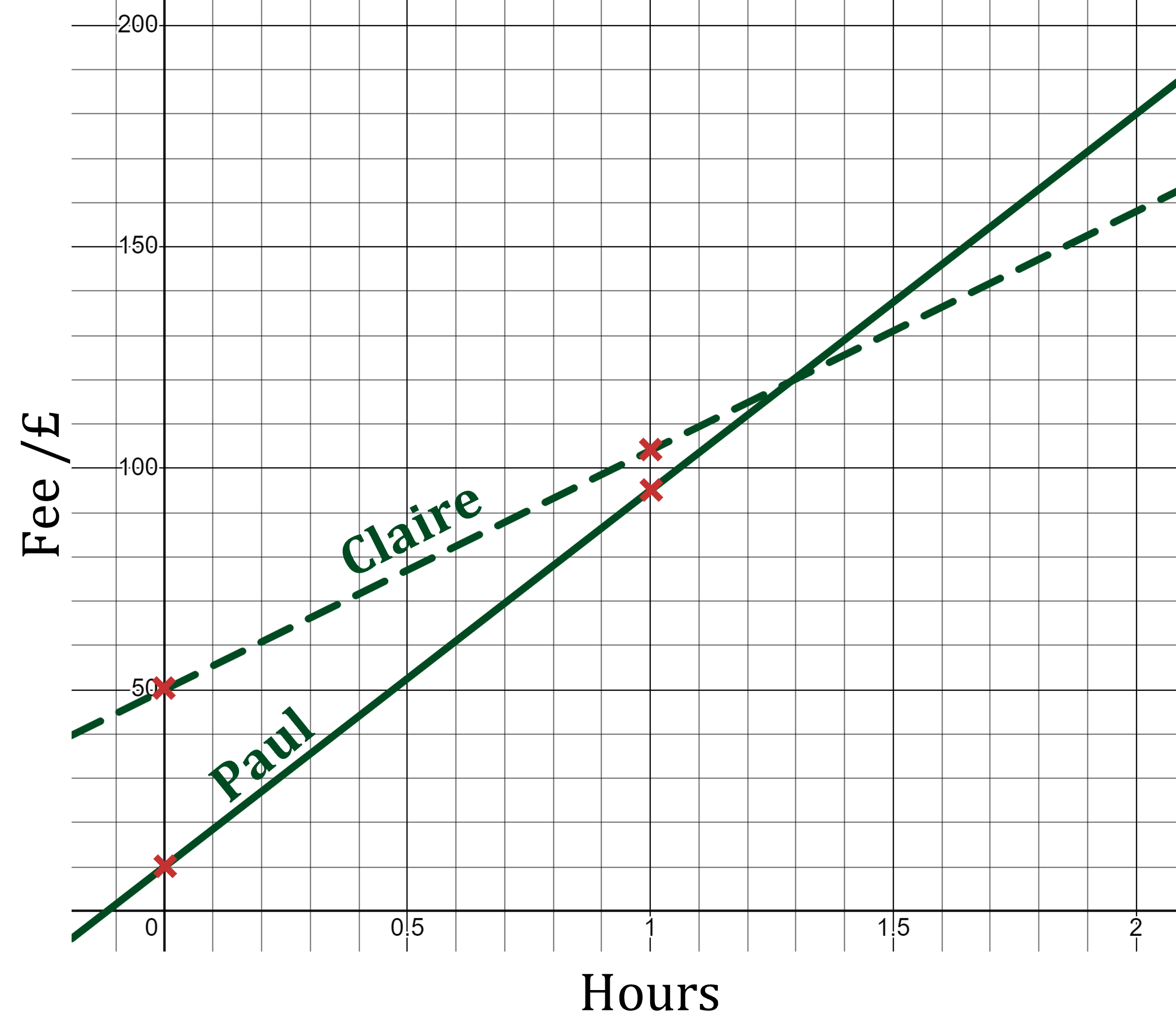
(a) Plot a line for each electrician showing the fee charged to customers for jobs lasting between 0 and 2 hours.

Show the number of hours on the $x$ -axis, and the fee on the $y$ -axis.

For Paul, the $y$ -intercept will be 10, as £10 is charged before a job is started (call-out fee)
The gradient for Paul will be 85, as £85 is charged per hour
The easiest points to plot are (0,10) and (1,95), and then join these to form a straight line

For Claire, the $y$ -intercept will be 50, and the gradient will be 54
Plot the points (0,50) and (1,104) and join them to form a straight line

Label the lines you plot

Two linear graphs; y=85x+10 and y=54x+50

(b) It is suggested that Paul is cheaper for a "short job" and Claire is cheaper for longer jobs.

Use your graph to find an approximate upper limit for the length of a "short job".

The point of intersection of the lines is where Paul and Claire charge the same amount in total, for the same length job

Read the point of intersection from the graph

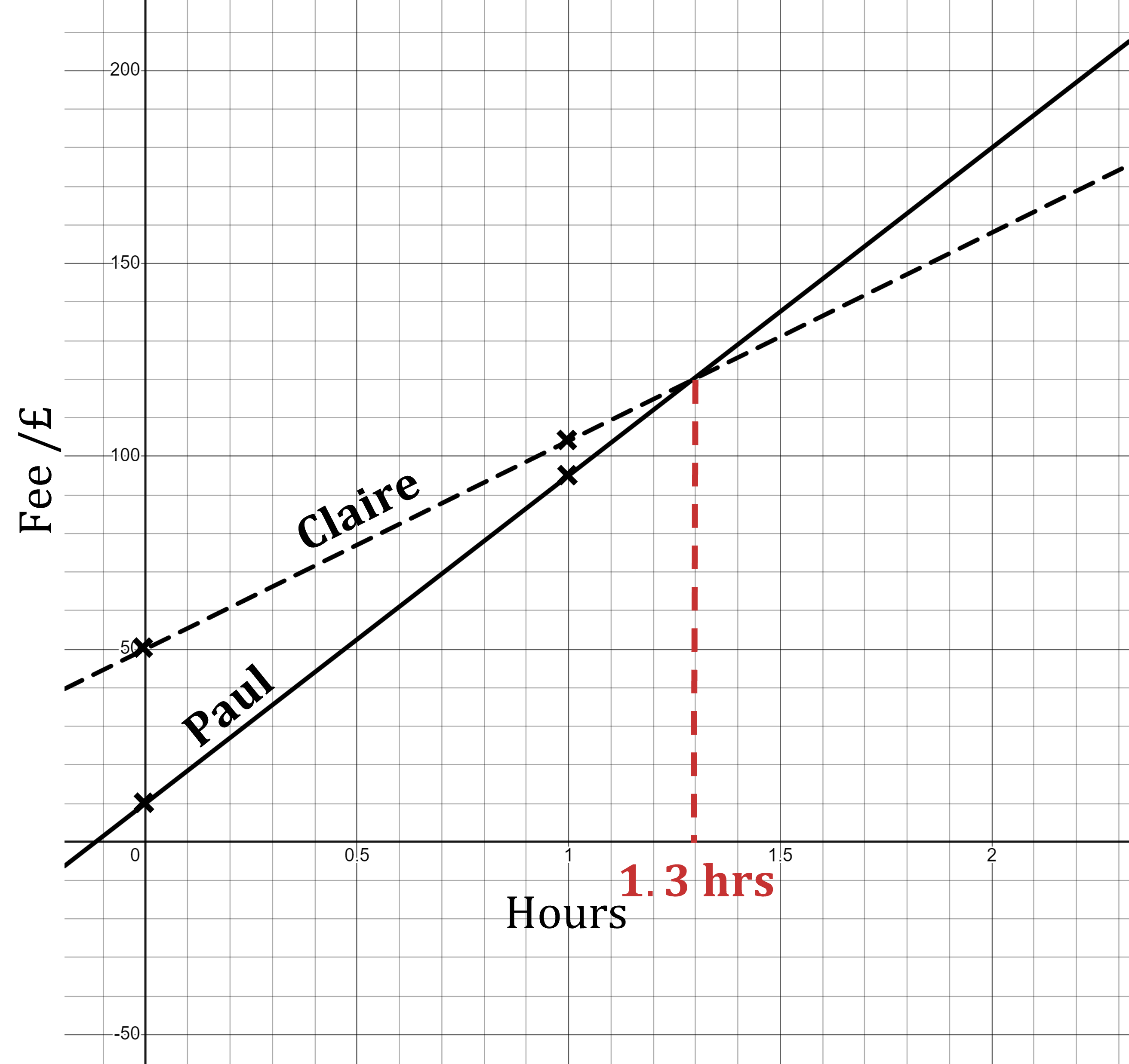
Finding x coordinate of intersection of y=85x+10 and y=54x+50, approximately x=1.3

For smaller values of $x$ than this, Paul's line is below Claire's, so Paul is cheaper

A short job is up to approximately 1.3 hours

The true value is 1.2903... hours that can be found using algebra
The question does not require you to find this however, it only asks you to approximate using the graph

Worked Example

Martina is using a graphical method to solve $2 x^{3} - 5 x^{2} - 6 x + 9 = 0$ .

She draws the graph of $y = 2 x^{3} - 5 x^{2}$ and a straight line graph on the same grid.

Here is the graph of $y = 2 x^{3} - 5 x^{2}$ .

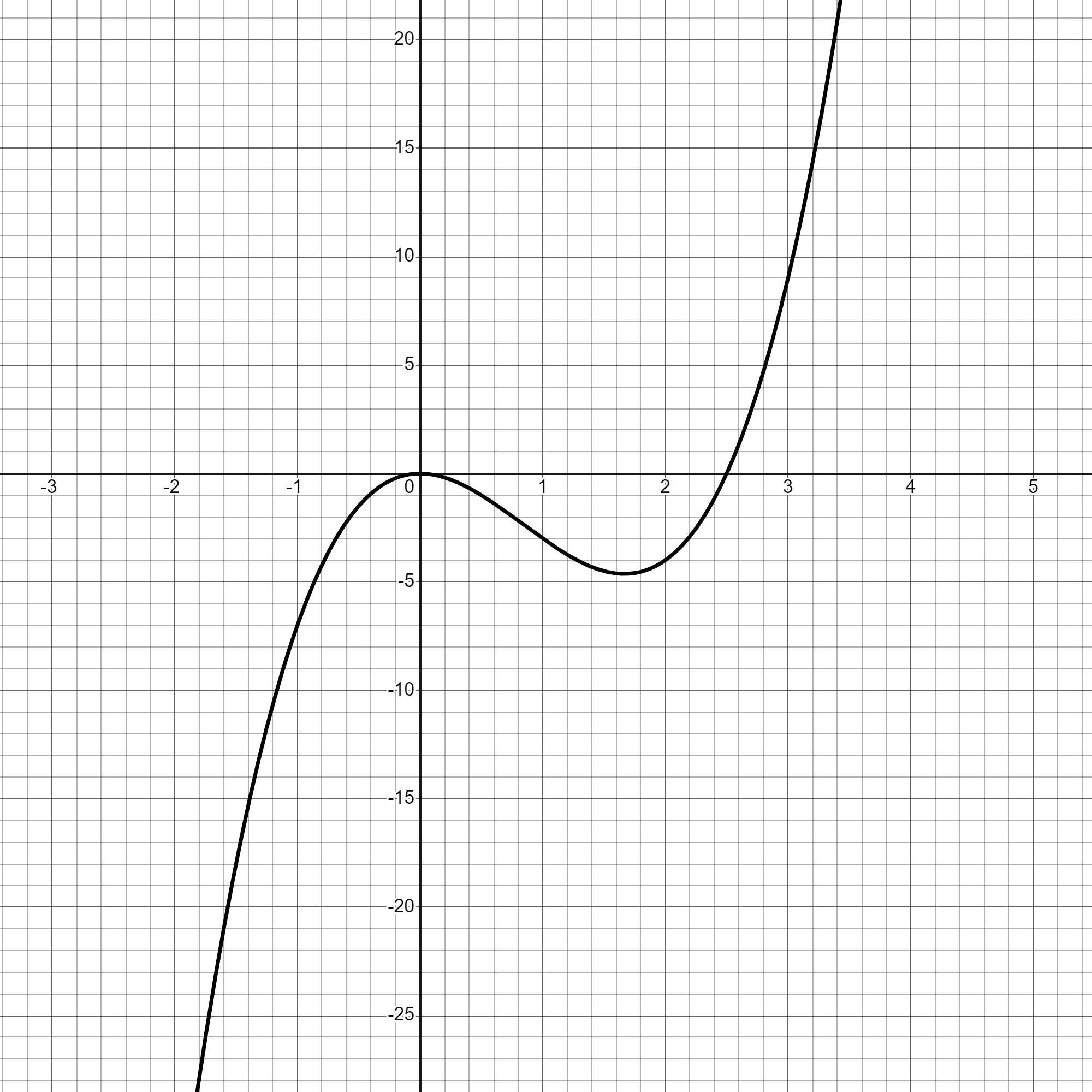
Complete her method to solve $2 x^{3} - 5 x^{2} - 6 x + 9 = 0$ .

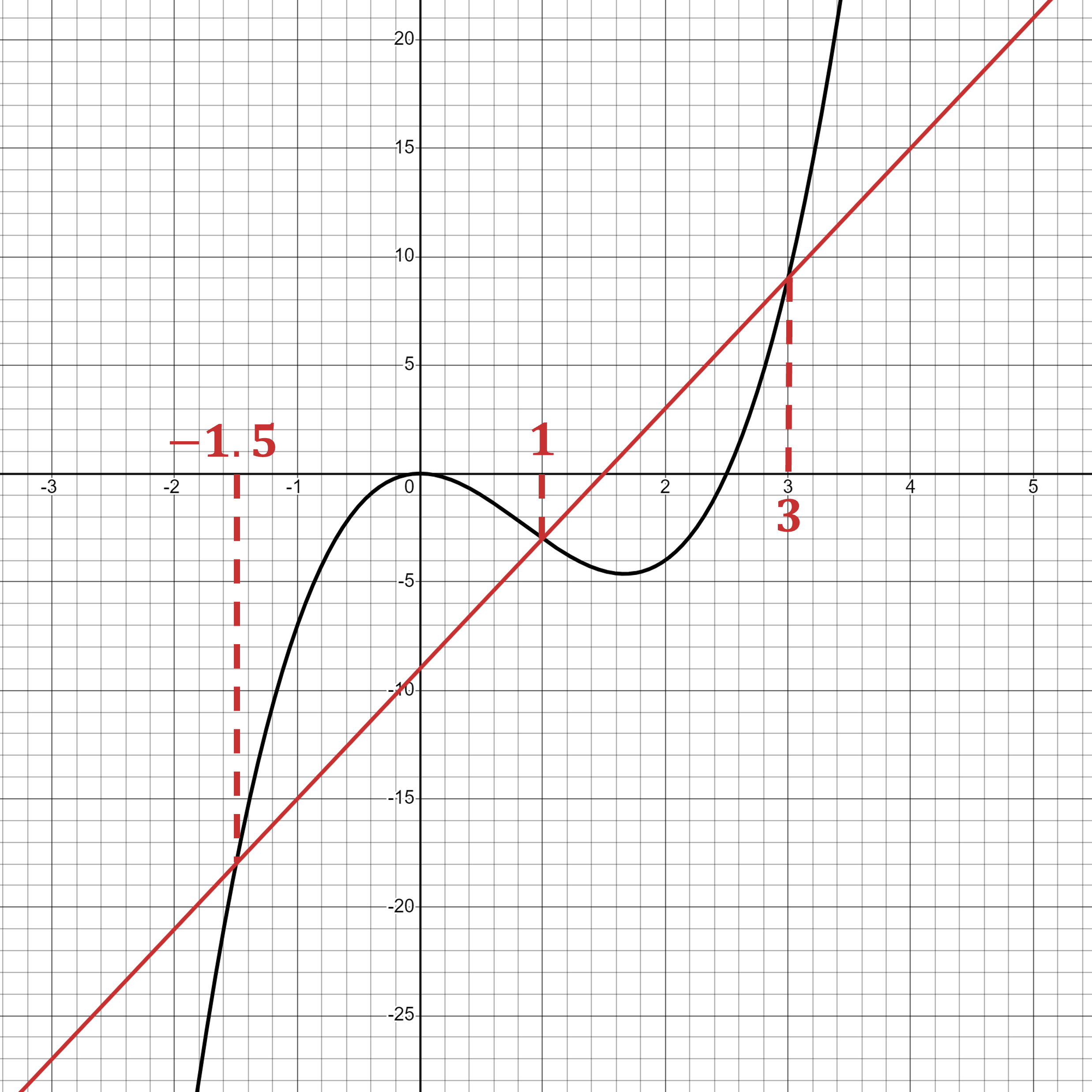
Rearrange $2 x^{3} - 5 x^{2} - 6 x + 9 = 0$ so that one side of the equation features the graph that has been plotted, $2 x^{3} - 5 x^{2}$

$\begin{array}{rcl} 2 x^{3} - 5 x^{2} - 6 x + 9 & = & 0 \\ 2 x^{3} - 5 x^{2} & = & 6 x - 9 \end{array}$

This shows that the solutions to $2 x^{3} - 5 x^{2} - 6 x + 9 = 0$ are the same as the solutions to $\begin{array}{rcl} 2 x^{3} - 5 x^{2} & = & 6 x - 9 \end{array}$

The solutions to $\begin{array}{rcl} 2 x^{3} - 5 x^{2} & = & 6 x - 9 \end{array}$ can be found by plotting the cubic $y = 2 x^{3} - 5 x^{2}$ , which is already plotted, and the straight line, $y = 6 x - 9$ , and then finding their points of intersection

As we are only solving an equation in terms of $x$ , we only need the $x$ -coordinates

intersection points of 2x^3 - 5x^2 and 6x-9 at x=-1.5, 1, and 3

$x = - 1.5 x = 1 x = 3$

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Shapes of Exponential GraphsNext:Modelling with Graphs

Points of Intersection (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note

Graphical Solutions

How do I use graphs to solve linear simultaneous equations?

How do I use graphs to solve simultaneous equations where one is a quadratic?

How do I use graphs to solve other equations?

Examiner Tips and Tricks

Worked Example

Worked Example

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Critical Analysis of Data & Models

Critical Analysis of Data & Models

Presenting Logical & Reasoned Arguments

Communicating Mathematical Approaches

Analysing Critically

Graphical Methods

Graphical Methods

Shapes of Linear, Quadratic & Cubic Graphs

Shapes of Exponential Graphs

Points of Intersection

Modelling with Graphs

Rates of Change

Rates of Change

Gradients & Rates of Change

Velocity & Acceleration

Exponential Functions

Exponential Functions

Exponential Functions & Logarithms

The Number e

Exponential Growth & Decay

Author: Jamie Wood

Reviewer: Dan Finlay