Revision NotesPast Papers
Level 3MathsAQAMathematical Studies (Core Maths)Paper 2C: Graphical TechniquesRevision NotesGraphical MethodsGraphical MethodsShapes of Exponential Graphs

Shapes of Exponential Graphs (AQA Level 3 Mathematical Studies (Core Maths)) : Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

Shapes of Exponential Graphs

What is an exponential?

  • An exponential is a function where the power is a variable, usually x

    • y equals 3 to the power of x is an example of an exponential

  • You may encounter exponentials in either of the following forms

    • y equals a to the power of x

    • y equals a to the power of negative x end exponent

    • Where a is a positive rational number, and x is a variable

    • All of the following are examples of exponentials

      • y equals 0.3 to the power of x

      • y equals 3.8 to the power of negative x end exponent

      • y equals 4.1 to the power of x

      • y equals 0.34 to the power of negative x end exponent

What does an exponential graph look like?

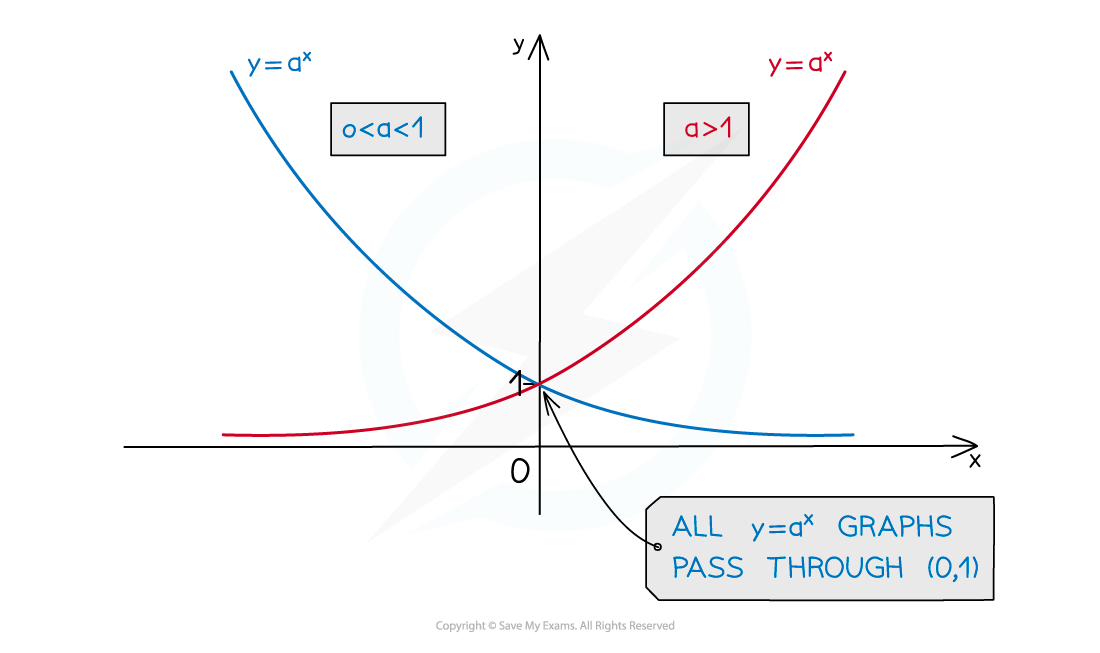
  • A graph of the form y equals a to the power of x where a is positive and larger than 1 will be increasing as x increases

    • y equals 5 to the power of x is increasing

  • A graph of the form y equals a to the power of italic minus x end exponent where a is positive and larger than 1 will be decreasing as x increases

    • y equals 7 to the power of negative x end exponent is decreasing

  • If a is between 0 and 1, then the opposite is true

    • y equals 0.4 to the power of x is decreasing

    • y equals 0.6 to the power of negative x end exponent is increasing

  • The bold italic y-intercept of y equals a to the power of x and y equals a to the power of negative x end exponent will be stretchy left parenthesis 0 comma space 1 stretchy right parenthesis

    • You can show this by substituting x equals 0 into the equation

    • Substituting x equals 0 into y equals a to the power of x or y equals a to the power of negative x end exponent will reduce both to y equals a to the power of 0 equals 1

  • The graphs do not cross the x-axis anywhere

  • Exponential graphs do not have any minimum or maximum points

    • They are either always increasing, or always decreasing

graphs of 3^x and 2^x
graphs of 0.3^x and 0.2^x

How can I find the equation of an exponential graph?

  • You may be given one or two co-ordinates that lie on a curve, and an approximate form for the equation of the graph

    • E.g. y equals a to the power of negative x end exponent or y equals k to the power of x

  • Remember that all co-ordinates on the curve must satisfy the equation

  • You can therefore substitute each coordinate into the given equation, and solve to find any unknown constants

Worked Example

C is a curve with an equation of the form  y equals a to the power of negative x end exponent where a is a positive constant.

C passes through the point (3, 125).

Find the value of y when x equals 7.

The value of a can be found by substituting the coordinate (3,125) into the equation

table row cell y space end cell equals cell space a to the power of negative x end exponent end cell row cell 125 space end cell equals cell space a to the power of negative 3 end exponent end cell end table

Solve to find a

Use laws of indices to rewrite the right hand side of the equation

table row 125 equals cell open parentheses a cubed close parentheses to the power of negative 1 end exponent end cell row 125 equals cell 1 over a cubed end cell end table

Multiply both sides by a cubed, and divide both sides by 125

table row cell 125 a cubed end cell equals 1 row cell a cubed end cell equals cell 1 over 125 end cell end table

Cube root to find a

a equals cube root of 1 over 125 end root equals 0.2

So the equation of curve C is

y equals 0.2 to the power of negative x end exponent

Find the value of y when x equals 7

y equals 0.2 to the power of negative 7 end exponent

y equals78 125


You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Shapes of Linear, Quadratic & Cubic GraphsNext:Points of Intersection
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.