Shapes of Linear, Quadratic & Cubic Graphs (AQA Level 3 Mathematical Studies (Core Maths)) : Revision Note

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on 2 May 2024

Shapes of Linear Graphs

What is the equation of a straight line?

$y = m x + c$ is the equation for any straight line
$m$ is gradient given by “difference in $y$ ” ÷ “difference in $x$ ”
- You may also see this written as $\frac{d y}{d x}$
$c$ is the y-axis intercept
An alternative form is $a x + b y + c = 0$
- Where $a$ , $b$ and $c$ are integers

linear graph showing y-axis, and how to calculate the gradient

How do I find the equation of a straight line?

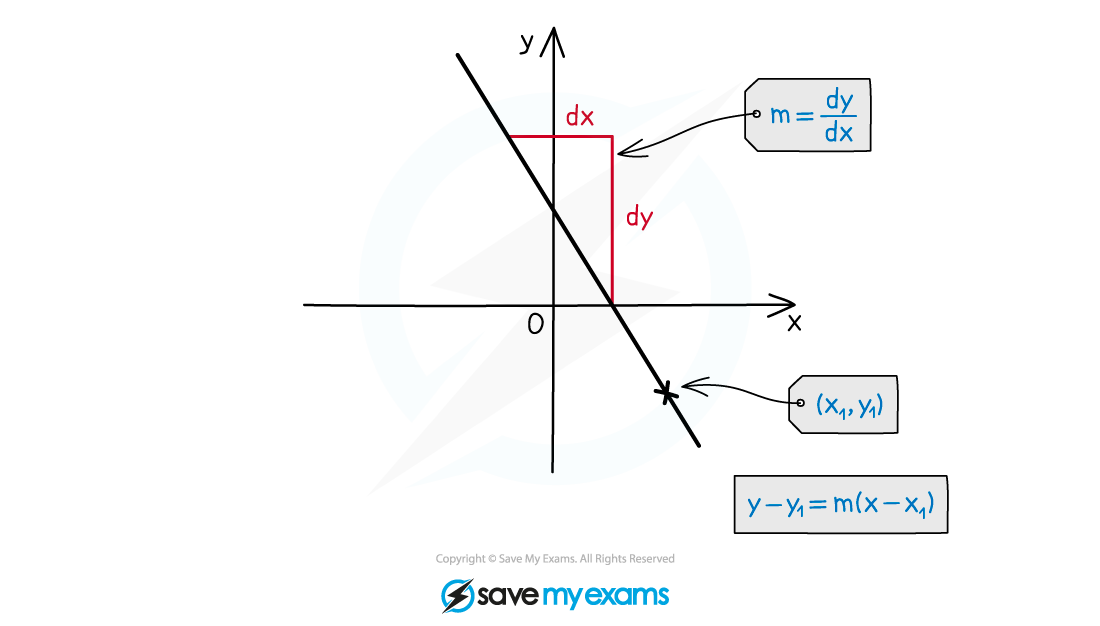
Linear graph with gradient and a point it passes through labelled

Two features of a straight line are needed
- Gradient, $m$
- A point the line passes through, $(x_{1}, y_{1})$

The equation can then be found using $y - y_{1} = m (x - x_{1})$
This can be arranged into either $y = m x + c$ or $a x + b y + c = 0$

Using a gradient and a point to write in y=mx+c or ax+by+c=0

How do I find the gradient of a straight line?

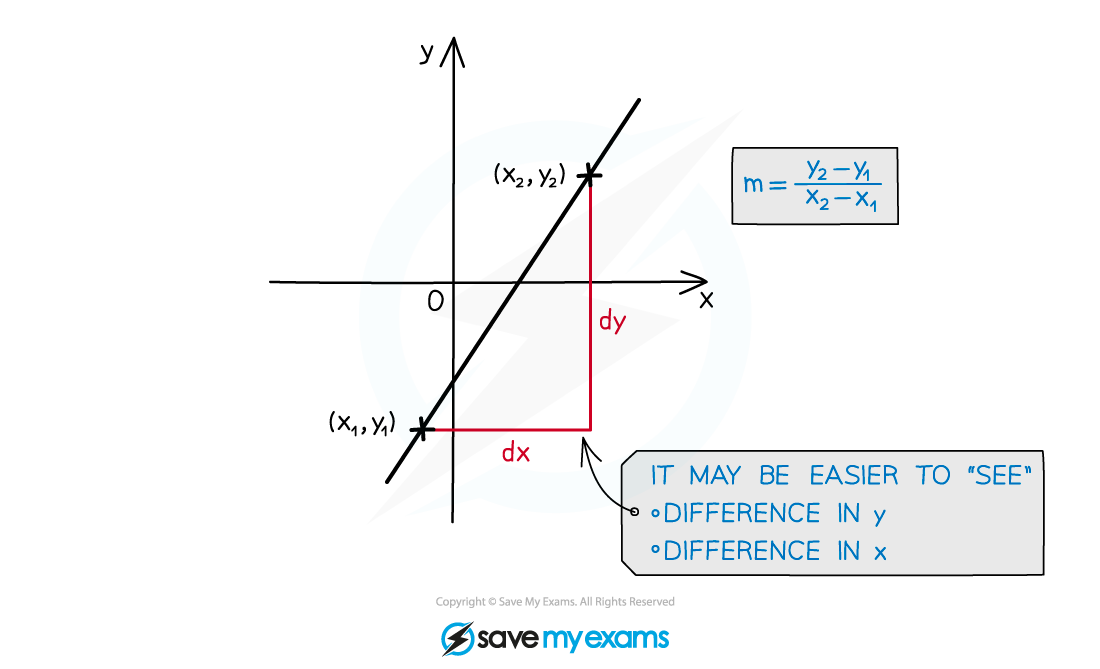
There are lots of ways to find the gradient of a line
Using two points on a line to find the change in $y$ divided by change in $x$

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

Gradient as change in y divided by change in x

Using the fact that lines are parallel or perpendicular to another line
- The gradient of parallel lines are equal
- The gradient of perpendicular lines are negative reciprocals of each other
  - E.g. $\frac{1}{3}$ and $- 3$

Gradients of parallel and perpendicular lines

Worked Example

The line $l$ passes through the points $(- 2, 5)$ and $(6, - 7)$ .

Find the equation of $l$ , giving your answer in the form $a x + b y = c$ where $a, b$ and $c$ are integers to be found.

First find the gradient of the line

$m = \frac{- 7 - 5}{6 - (- 2)} = \frac{- 12}{8} = - \frac{3}{2}$

Substitute the gradient and the coordinates of one of the points into $y - y_{1} = m (x - x_{1})$

$\begin{array}{rcl} y - 5 & = & - \frac{3}{2} (x - (- 2)) \\ y - 5 & = & - \frac{3}{2} (x + 2) \\ y - 5 & = & - \frac{3}{2} x - 3 \end{array}$

Multiply both sides of the equation by 2 to get rid of the fraction

$\begin{array}{rcl} 2 (y - 5) & = & 2 (- \frac{3}{2} x - 3) \\ 2 y - 10 & = & - 3 x - 6 \end{array}$

Rearrange into the required form

$3 x + 2 y = 4$

Shapes of Quadratic Graphs

What is a quadratic?

A quadratic is a function of the form $y = a x^{2} + b x + c$ where $a$ is not zero
- They are a very common type of function in mathematics, so it is important to know their key features

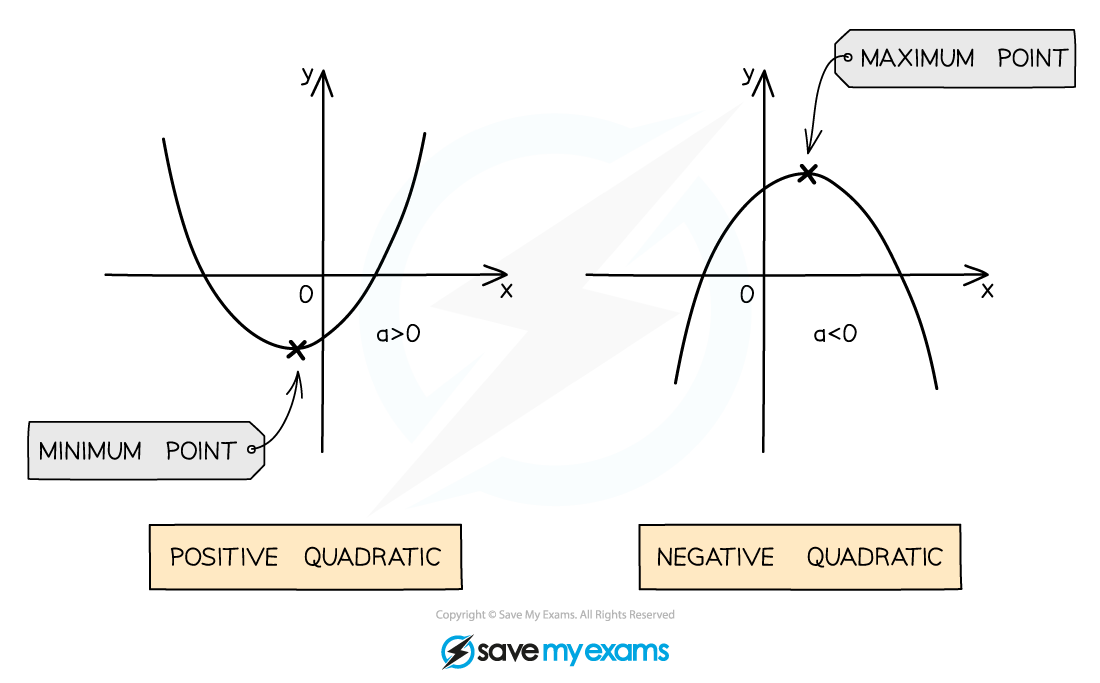
What does a quadratic graph look like?

The shape made by a quadratic graph is known as a parabola
The parabola shape of a quadratic graph can either look like a “u-shape” or an “n-shape”
- A quadratic with a positive coefficient of $x^{2}$ will be a u-shape
- A quadratic with a negative coefficient of $x^{2}$ will be an n-shape
A quadratic will always cross the $y$ -axis
A quadratic may cross the $x$ -axis twice, once, or not at all
- The points where the graph crosses the $x$ -axis are called the roots
If the quadratic is a u-shape, it has a minimum point (the bottom of the u)
If the quadratic is an n-shape, it has a maximum point (the top of the n)
Minimum and maximum points are both examples of turning points

A u shaped graph which is a positive quadratic, and an n shaped graph which is a negative quadratic

How do I sketch a quadratic graph?

We could create a table of values for the function and then plot it accurately, however we often only require a sketch to be drawn, showing just the key features
The most important features of a quadratic are
- Its overall shape; a u-shape or an n-shape
- Its $y$ -intercept
- Its $x$ -intercept(s), these are also known as the roots
- Its minimum or maximum point (turning point)
If it is a positive quadratic ( $a$ in $a x^{2} + b x + c$ is positive) it will be a u-shape
If it is a negative quadratic ( $a$ in $a x^{2} + b x + c$ is negative) it will be an n-shape
The $y$ -intercept of $y = a x^{2} + b x + c$ will be $(0, c)$
The roots, or the $x$ -intercepts will be the solutions to $y = 0$ ; $a x^{2} + b x + c = 0$
- You can solve a quadratic by factorising, completing the square, or using the quadratic formula
- There may be 2, 1, or 0 solutions and therefore 2, 1, or 0 roots
The minimum or maximum point of a quadratic can be found by completing the square
- Once the quadratic has been written in the form $y = p {(x - q)}^{2} + r$ , the minimum or maximum point is given by $(q, r)$
- Be careful with the sign of the x-coordinate
  - E.g. if the equation is $y = {(x - 3)}^{2} + 2$ then the minimum point is $(3, 2)$ but if the equation is $y = {(x + 3)}^{2} + 2$ then the minimum point is $(- 3, 2)$

Worked Example

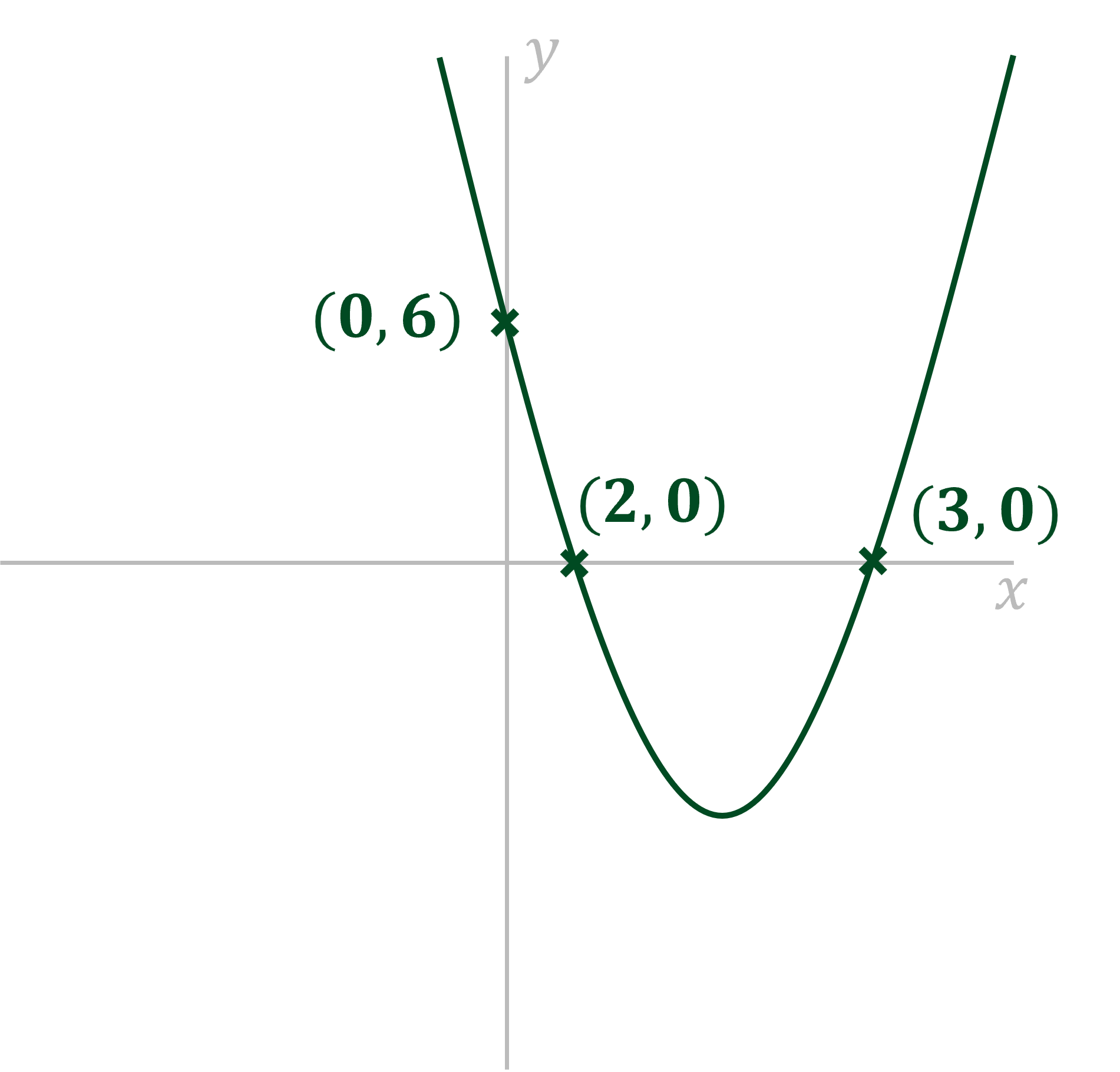
(a) Sketch the graph of $y = x^{2} - 5 x + 6$ showing the $x$ and $y$ intercepts.

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at

(0,6)

Factorise

$y = (x - 2) (x - 3)$

Solve $y = 0$

$(x - 2) (x - 3) = 0$

$x = 2 or x = 3$

So the roots of the graph are

(2,0) and (3,0)

(b) Sketch the graph of $y = x^{2} - 6 x + 13$ showing the $y$ -intercept and the turning point.

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the y-axis at

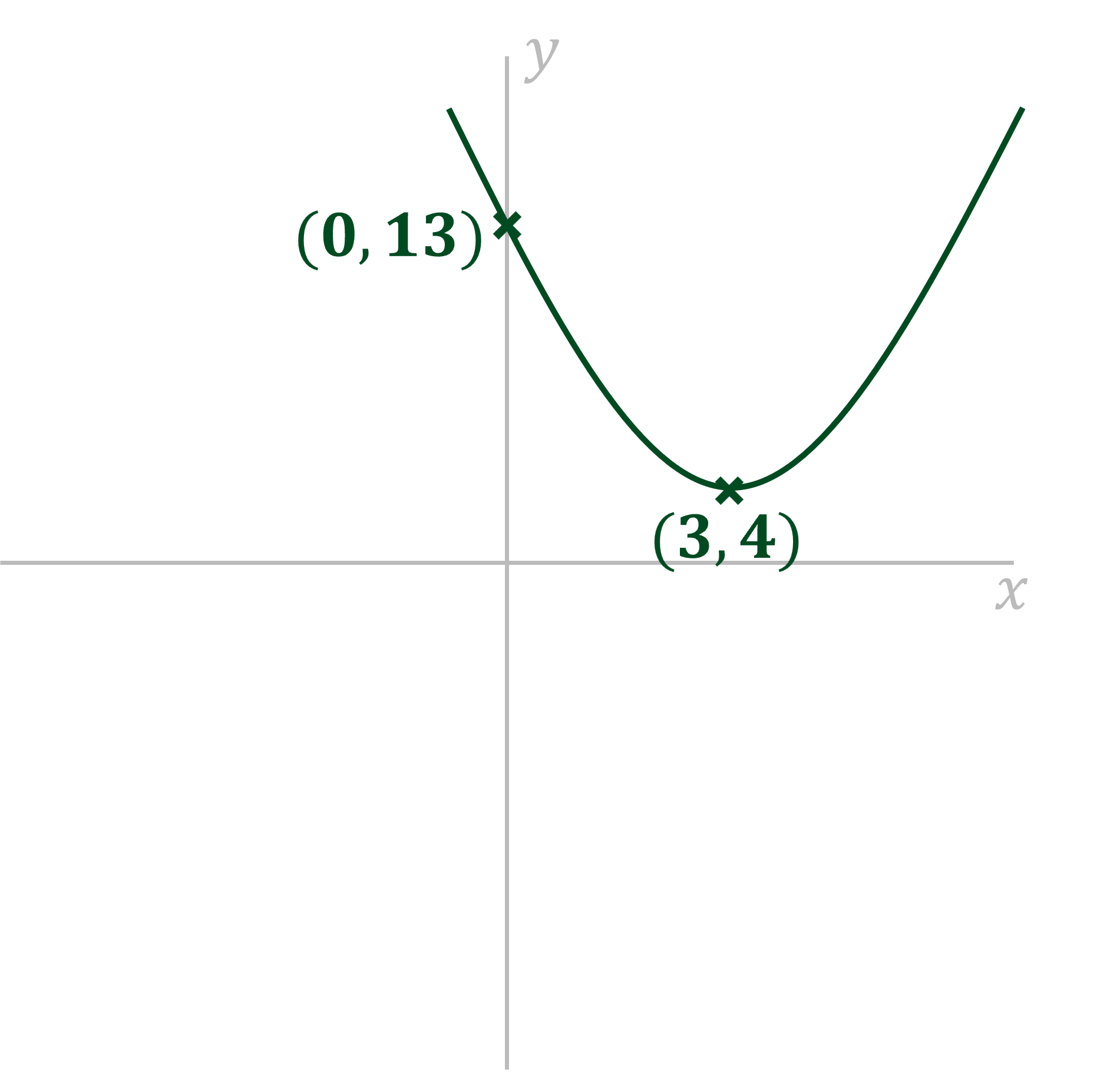
(0,13)

We can find the minimum point (it will be a minimum as it is a positive quadratic) by completing the square

$\begin{array}{rcl} x^{2} - 6 x + 13 & = & {(x - 3)}^{2} - 9 + 13 \\ = & {(x - 3)}^{2} + 4 \end{array}$

This shows that the minimum point will be

(3,4)

As the minimum point is above the $x$ -axis, this means the graph will not cross the $x$ -axis, i.e. it has no roots

We could also show that there are no roots by trying to solve $x^{2} - 6 x + 13 = 0$

If we use the quadratic formula, we will find that $x$ is the square root of a negative number
This is not a real number, which means there are no real solutions, and hence there are no roots

It is a negative quadratic, so will be an n-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at

(0, -4)

We can find the maximum point (it will be a maximum as it is a negative quadratic) by completing the square

$- x^{2} - 4 x - 4 = - 1 (x^{2} + 4 x + 4) = - 1 ({(x + 2)}^{2} - 4 + 4) = - {(x + 2)}^{2}$

This shows that the maximum point will be

(-2, 0)

As the maximum is on the $x$ -axis, there is only one root

We could also show that there is only one root by solving $- x^{2} - 4 x - 4 = 0$

If you use the quadratic formula, you will find that the two solutions for $x$ are the same number; in this case -2

Shapes of Cubic Graphs

What is a cubic?

A cubic polynomial is a function of the form $a x^{3} + b x^{2} + c x + d$
- $a, b, c$ and $d$ are constants
- It is a polynomial of degree 3
  - So $b, c$ and/or $d$ could be zero
To sketch the graph of a cubic polynomial it will need to be in factorised form
- E.g. $(2 x - 1) (x + 2) (x - 3)$ is the factorised form of $2 x^{3} - 3 x^{2} - 11 x + 6$

What does the graph of a cubic polynomial look like?

In general the graph of a cubic polynomial will take one of the four forms
- All are smooth curves that take some practice to sketch!

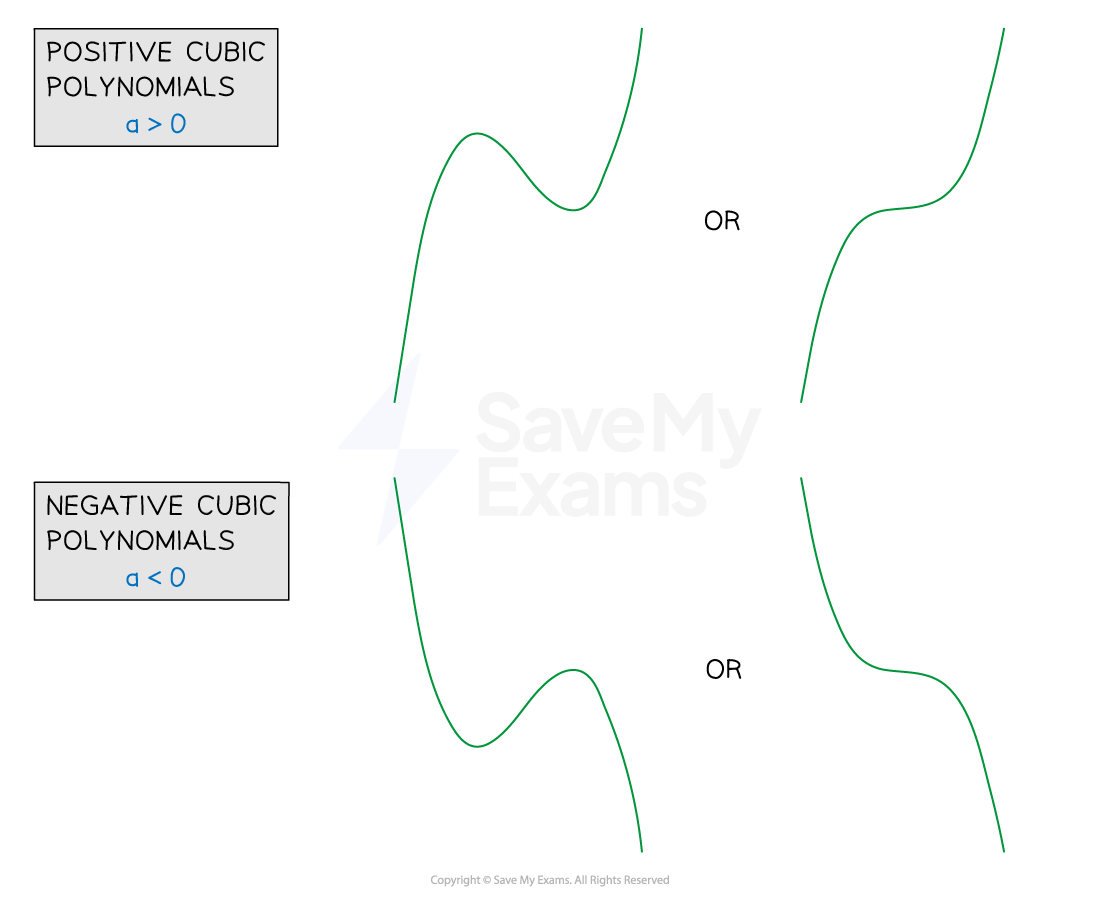
general shape of positive and negative cubic graphs

The exact form a particular cubic polynomial will depend on:
- The number (and value) of roots ( $x$ -axis intercepts) of the cubic polynomial
- The $y$ -axis intercept
- The sign of the coefficient of the $x^{3}$ term ( $a$ )
  - If $a > 0$ the graph is a positive cubic ('starts' in the third quadrant, 'ends' in the first)
  - If $a < 0$ the graph is a negative cubic ('starts' in the second quadrant, 'ends' in the fourth)
- The turning points

Key features of a polynomial graph - shape, intercept, turning points

How do I sketch the graph of a cubic polynomial?

STEP 1
Find the $y$ -axis intercept by setting $x = 0$
STEP 2
Find the $x$ -axis intercepts (roots) by setting $y = 0$
Any repeated roots will mean the graph touches, rather than crosses, the $x$ -axis
STEP 3
Consider the shape of the graph; is it a positive cubic or a negative cubic?
Where does the graph 'start' and 'end'?
STEP 4
Consider where any turning points should go
STEP 5
Sketch the graph with a smooth curve, labelling points where the graph intercepts the $x$ and $y$ axes

Worked Example

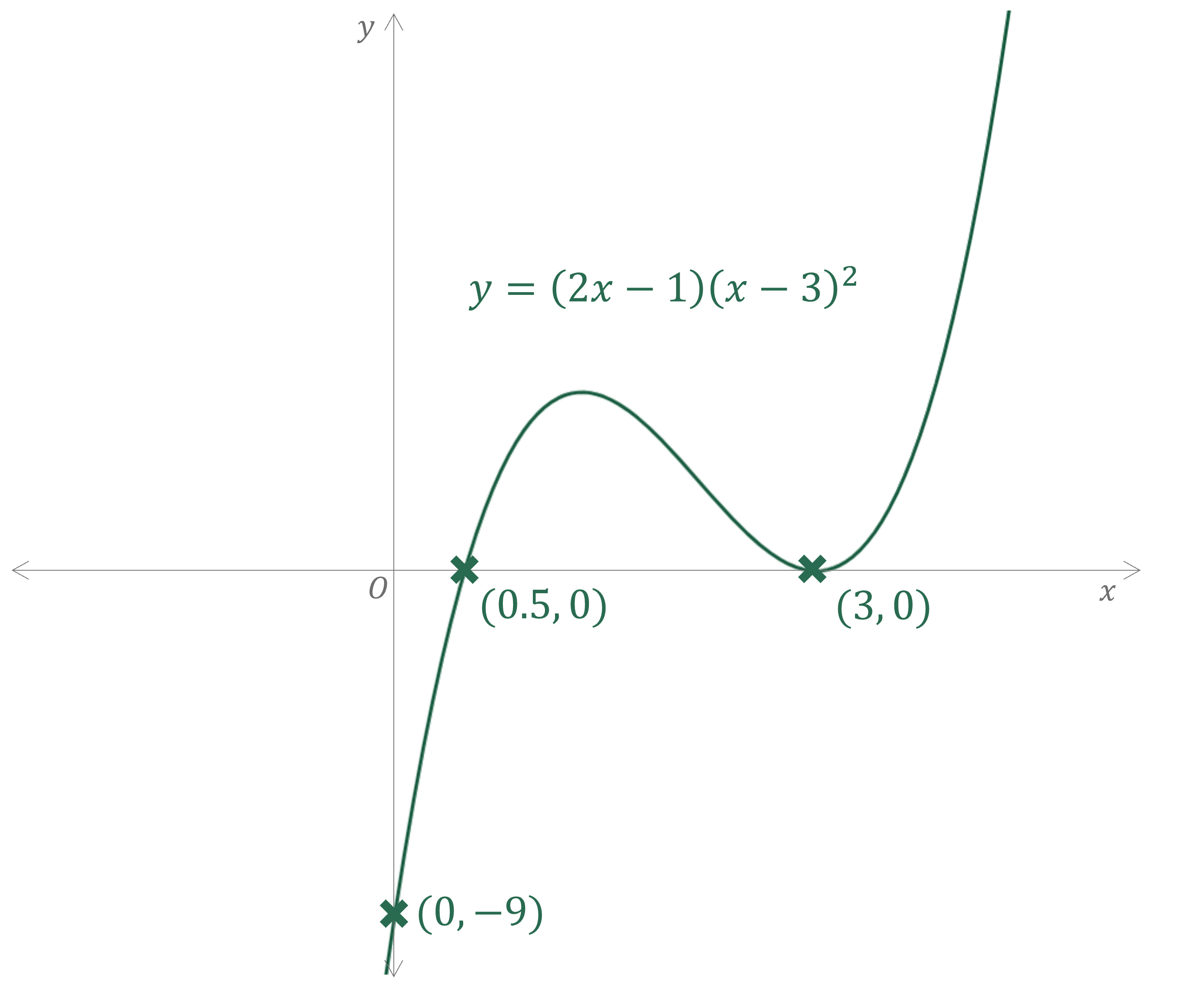
Sketch the graph of $y = (2 x - 1) {(x - 3)}^{2}$ .

Find the $y$ -axis intercept by substituting in $x = 0$

$y = (- 1) {(- 3)}^{2} = - 9$

Find the $x$ -axis intercepts by solving $y = 0$
Either bracket can be equal to zero

$\begin{array}{rcl} (2 x - 1) & = & 0 \\ x & = & \frac{1}{2} \end{array}$

$\begin{array}{rcl} {(x - 3)}^{2} & = & 0 \\ x & = & 3 \end{array}$
(repeated solution, as there are two $(x - 3)$ brackets

Consider the shape, and the 'start' and 'end' points

$a > 0 (a = 2)$ so it is a positive cubic
$x = 3$ is a repeated root so the graph will touch the $x$ -axis at this point

Consider the turning points

One turning point (minimum) will need to be where the curve touches the $x$ -axis
The other (maximum) will need to be between the two roots $x = \frac{1}{2}$ and $x = 3$

Sketch a smooth curve with labelled intercepts

worked example - final answer sketch of cubic showing intersections

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Analysing CriticallyNext:Shapes of Exponential Graphs

Shapes of Linear, Quadratic & Cubic Graphs (AQA Level 3 Mathematical Studies (Core Maths)) : Revision Note

Shapes of Linear Graphs

What is the equation of a straight line?

How do I find the equation of a straight line?

How do I find the gradient of a straight line?

Shapes of Quadratic Graphs

What is a quadratic?

What does a quadratic graph look like?

How do I sketch a quadratic graph?

Shapes of Cubic Graphs

What is a cubic?

What does the graph of a cubic polynomial look like?

How do I sketch the graph of a cubic polynomial?

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Critical Analysis of Data & Models

Critical Analysis of Data & Models

Presenting Logical & Reasoned Arguments

Communicating Mathematical Approaches

Analysing Critically

Graphical Methods

Graphical Methods

Shapes of Linear, Quadratic & Cubic Graphs

Shapes of Exponential Graphs

Points of Intersection

Modelling with Graphs

Rates of Change

Rates of Change

Gradients & Rates of Change

Velocity & Acceleration

Exponential Functions

Exponential Functions

Exponential Functions & Logarithms

The Number e

Exponential Growth & Decay

Author: Jamie Wood

Reviewer: Dan Finlay