Velocity & Acceleration (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note

Distance-time Graphs

How do I use a distance-time graph?

• Distance-time graphs show the distance travelled at different times

  • Distance is on the vertical axis

  • Time is on the horizontal axis 

• The gradient of the graph is the speed

  • 

  • The units for speed are usually metres per second

    • Or m/s or ms^-1

• The steeper the line or curve, the faster the object is moving

  • Lines or curves with positive gradients represent objects moving away from the start point

  • Lines or curves with negative gradients represent objects moving towards the start point

  • Lines that are horizontal represent rest

    • The object is stationary (not moving)

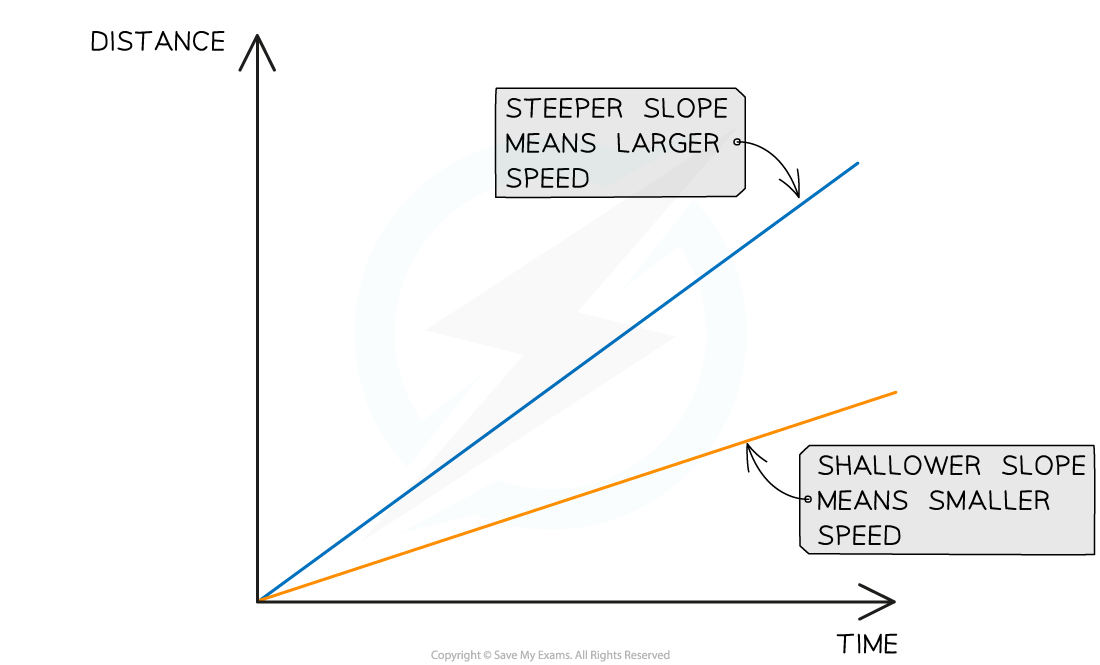
• Remember that the gradient of a distance-time graph is equal to the speed

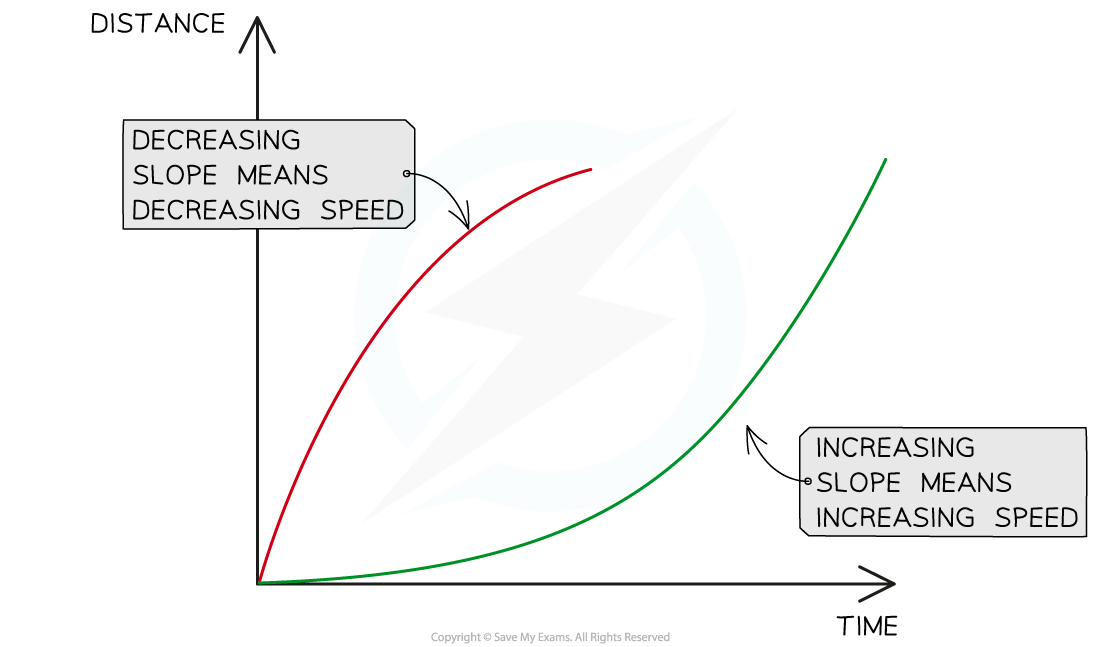
  • If the gradient decreases (becomes less steep) the speed is decreasing

  • If the gradient increase (becomes more steep) the speed is increasing

How do I work out the overall average speed?

• The overall average speed for the whole journey is

• The total time includes any rests

• This can be applied to journeys with multiple parts

How do I work with curved distance-time graphs?

• The gradient of a linear distance-time graph is constant

  • This means the speed is constant throughout

  • It is equal to the average speed for the journey

• A curved distance-time graph has a gradient which is constantly changing

  • This means the speed is constantly changing

• The gradient can be estimated at a point to find the speed at that point in time

  • This is done by drawing a tangent at that point and finding its gradient

• The gradient can also be estimated between two points (using a chord) to find the average speed between those two points

• See Gradients & Rates of Change for how to do this

• If a curve has a point where the tangent is horizontal (a stationary point) it may be referred to as "instantaneously at rest"

  • At a stationary point, the object will be changing direction

  • This is because the gradient (speed) will be changing from positive to negative, or vice-versa

Velocity-time Graphs

What is a velocity-time graph?

• Velocity describes the speed and direction of an object

  • E.g. A velocity of -3 ms^-1 is equivalent to a speed of 3 ms^-1

• You may see speed-time graphs or velocity-time graphs

  • The direction that an object is travelling in does not matter for a speed-time graph

  • Speed-time graphs and velocity-time graphs follow the same principles

• Velocity-time graphs show the velocity of an object at different times

  • Velocity is on the vertical axis

  • Time is on the horizontal axis 

• The gradient of the graph is the acceleration

  • 

  • The units for acceleration are usually metres per second squared

    • Or m/s² or ms^-2

• The steeper the line or curve, the faster the object is accelerating

  • Lines or curves with positive gradients above the x-axis, represent objects increasing their velocity (accelerating)

  • Lines or curves with negative gradients above the x-axis, represent objects decreasing their velocity (decelerating)

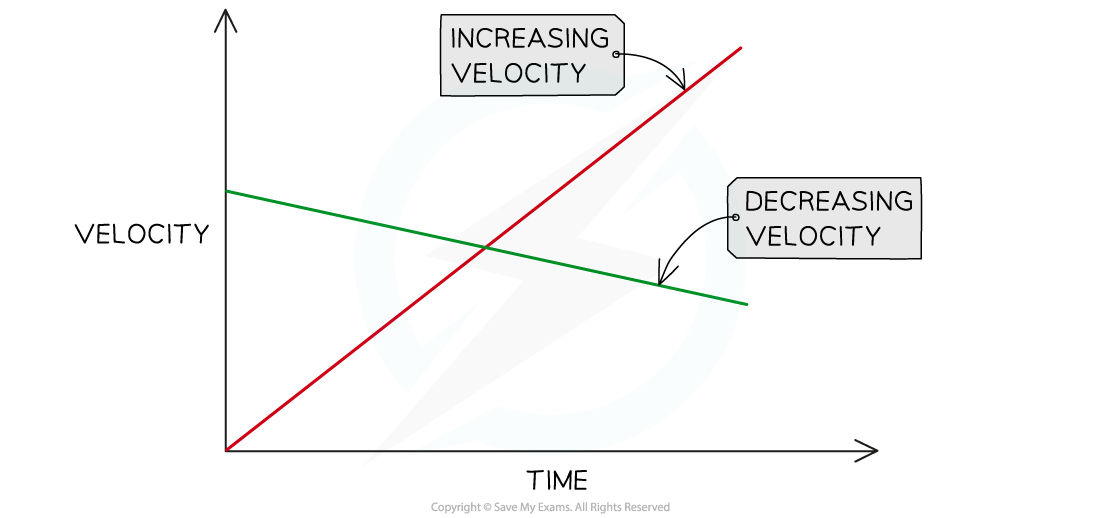
• Lines that are horizontal represent constant speed

• The object is at rest at points on the horizontal axis (where speed is zero)

How do I work with curved velocity-time graphs?

• The gradient of a linear velocity-time graph is constant

  • This means the acceleration is constant throughout

  • It is equal to the average acceleration for the journey

• A curved velocity-time graph has a gradient which is constantly changing

  • This means the acceleration is constantly changing

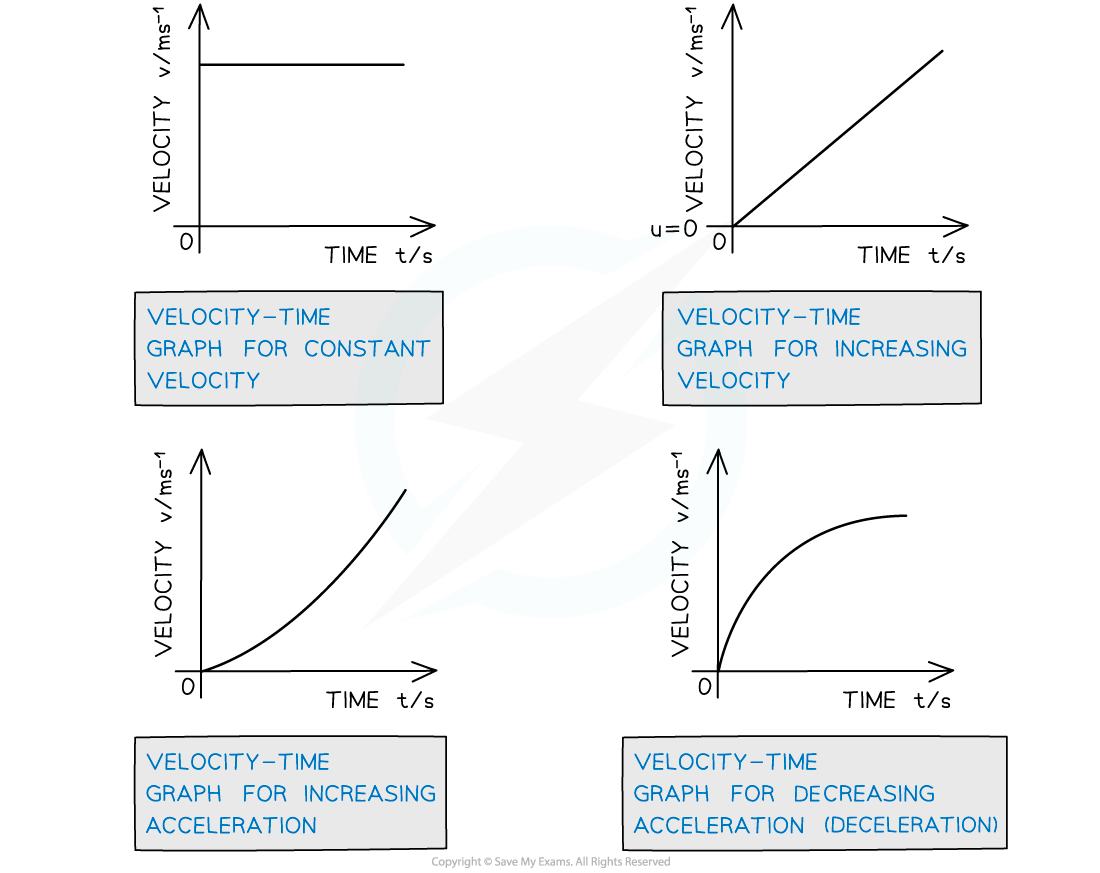
• The gradient can be estimated at a point to find the acceleration at that point in time

  • This is done by drawing a tangent at that point and finding its gradient

• The gradient can also be estimated between two points (using a chord) to find the average acceleration between those two points

• See Gradients & Rates of Change for how to do this