Calculus with Polar Coordinates (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Finding tangents to polar curves
What is the gradient/tangent of a polar curve?
Gradients (and tangents) are the same as using Cartesian coordinates
i.e. a gradient of 1 in Cartesian coordinates is still a gradient of 1 in polar coordinates
a 45° line from “bottom left” to “top right” is a gradient of 1 in both systems
the equation of a tangent to a polar curve should be written in polar form
How do I find the tangents to a polar curve?
Finding the gradient - and so the equation of a tangent - to a polar curve is based on parametric differentiation in Cartesian form
Since
,
and
, it follows that
Then, using parametirc differentiation the gradient is given by
From which the Cartesian equation can be found
Which can then be converted into polar form using
and
How do I find horizontal and vertical tangents to a polar curve?
Many questions only concern tangents that are horizontal and/or vertical to the curve
Horizontal tangents are described as being “parallel to the initial line”
Horizontal tangents occur where
Vertical tangents are described as being “perpendicular to the initial line”
Vertical tangents occur where
Questions require finding the coordinates of points that have horizontal or vertical tangents (rather than finding the equations of the tangents)
Coordinates should be in polar form, i.e.
In some cases, both
and
at a particular point
Under these cases the polar curve has a cusp
But vice versa is not necessarily true
A polar curve with a cusp does not necessarily mean
and
Examiner Tips and Tricks
If not provided, sketch the graph of the polar curve
This will help you to spot how many horizontal/vertical tangents there are
You could use a graphical calculator to help you do this
Worked Example
A sketch of the polar curve , with equation
, where
is shown below.
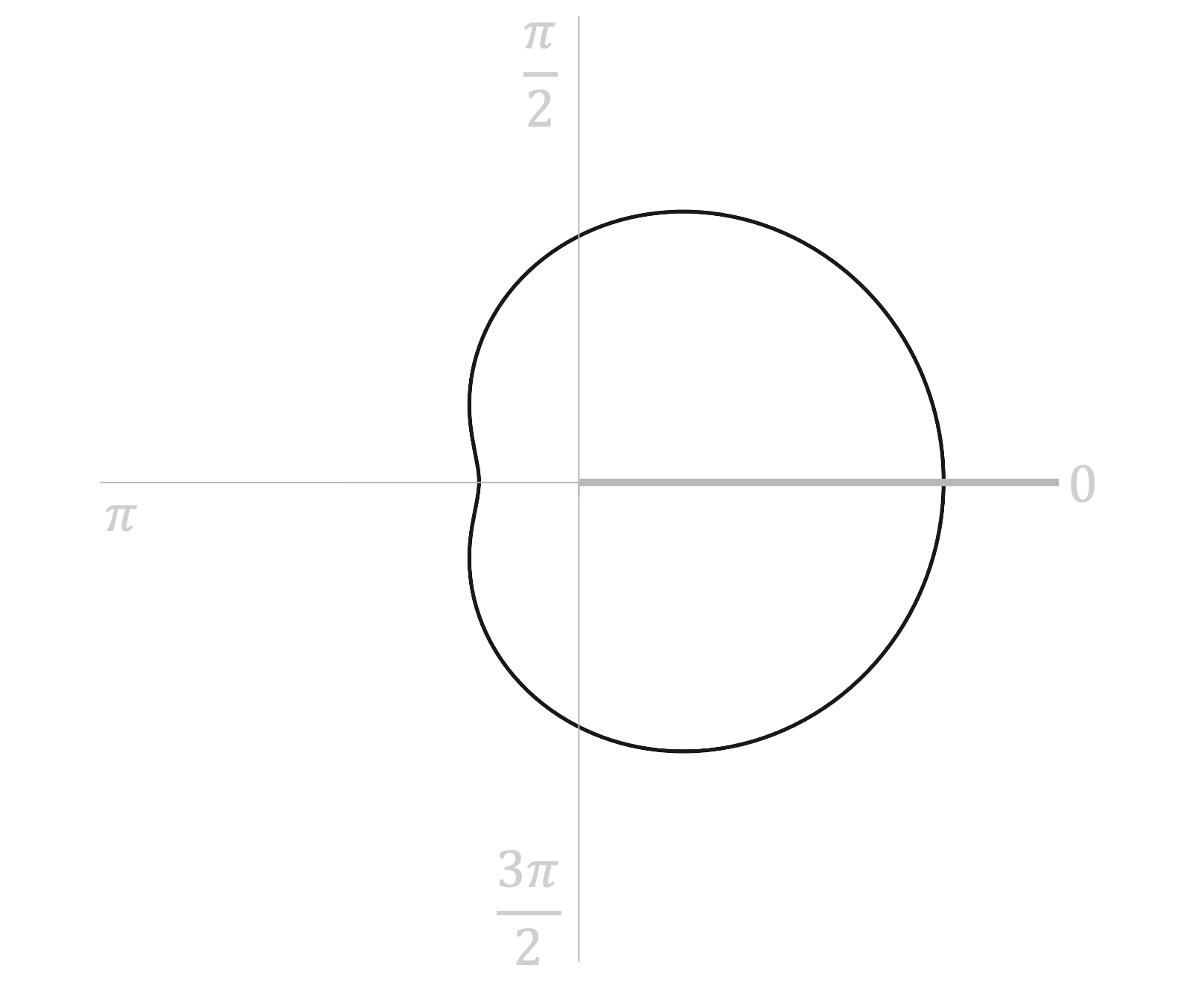
Find the coordinates of the points on where the tangents are (i) parallel, (ii) perpendicular to the initial line, giving values to 2 significant figures where appropriate.
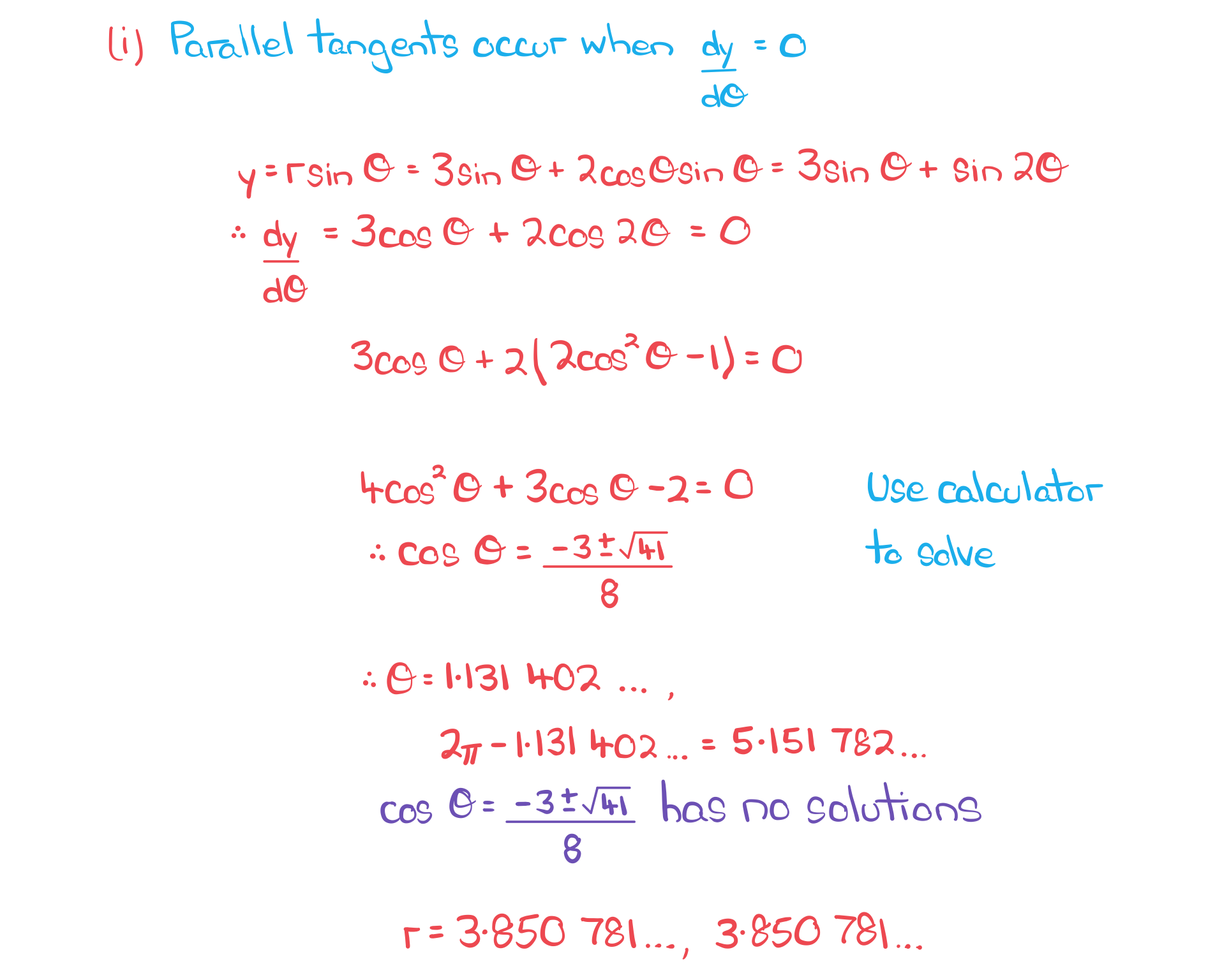

Finding areas enclosed by polar curves
To find the area enclosed by a polar curve (or part of) it is first crucial to know how to find the area of a sector in polar coordinates
How do I find the area of a sector given by a polar curve?
In polar coordinates, the area of a sector, A, is given by
where and
The sector is bounded by the curve
and the two half-lines
and
This is given in the formula booklet
If
is constant then the formula gives the area of the sector of a circle with centre angle
What is meant by the area enclosed by a polar curve?
The area enclosed by a polar curve refers to an area bounded by a curve
between the half-lines
and
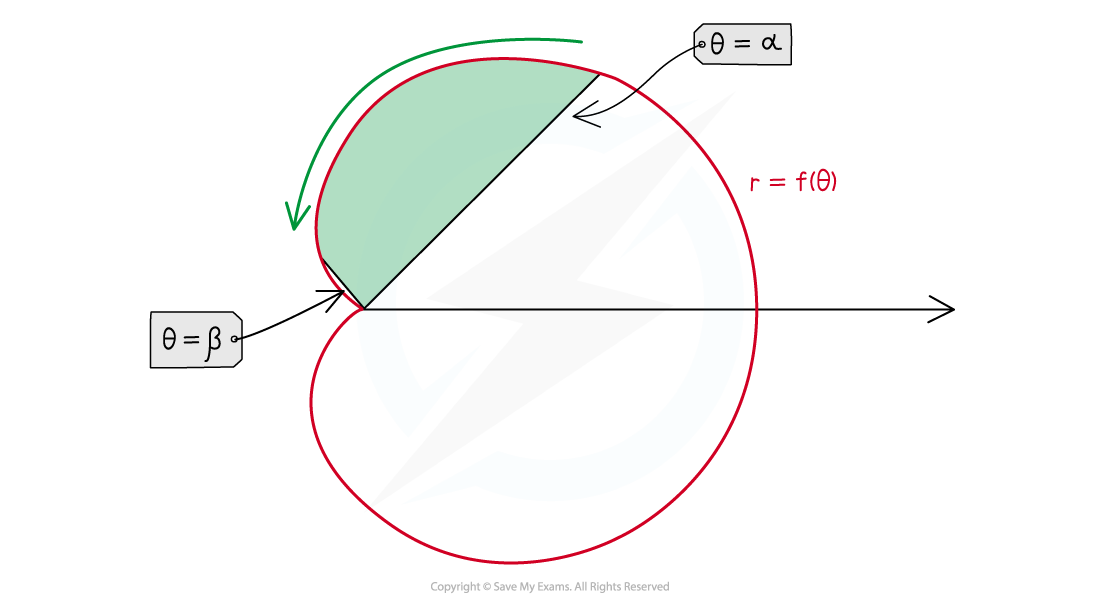
This can be considered as the area created by a 'sweeping' hand of a clock (but going anticlockwise!) moving between
and
The integral calculates the sum of an infinite number of sectors which start at
and end at
This is the polar equivalent of the sum of an infinite number of rectangles under a curve in Cartesian coordinates
How do I find the area enclosed by a polar curve?
STEP 1
If not given, a sketch of the curve is helpful
Identify the half-linesand
between which the area lies
This may involve solving equations
Always look for symmetry – many problems can be found by finding “half the area” and “doubling” – for example only finding an area above the initial lineSTEP 2
Findand manipulate it into an integrable form This may involve using trigonometric identities and/or common integration techniques such as reverse chain rule, 'adjust and compensate'
Set up the integral using the formulaSTEP 3
Evaluate the integral and interpret the answer Remember to double/scale-up the integral value to find the area if symmetry has been used
Examiner Tips and Tricks
The use of symmetry in these problems can make them a lot easier so do always look to use it
Calculators may be able to evaluate integrals but remember they usually expect x to be the ‘input’ variable
Calculators may not always produce exact values so check what is required by the question
Worked Example
Find the exact area of one loop of the curve with polar equation .

Finding areas enclosed by multiple polar curves
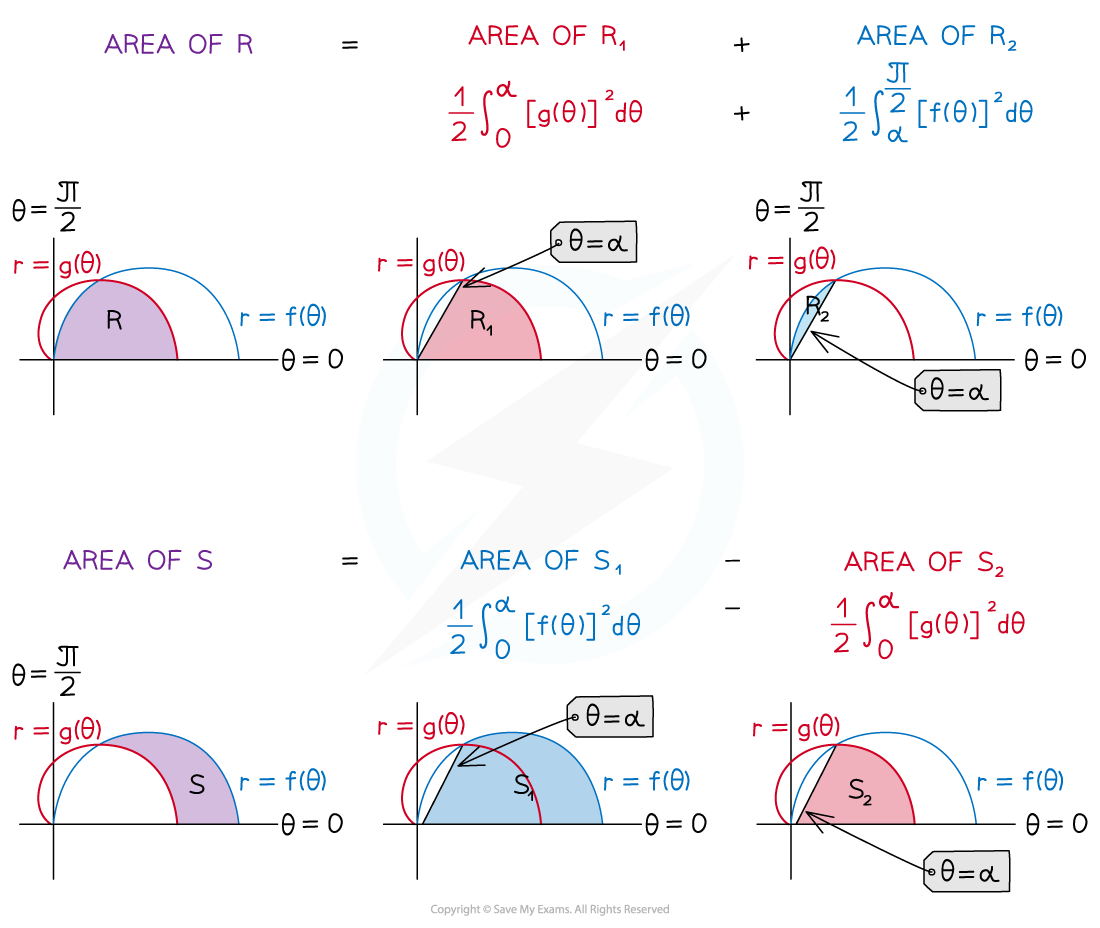
What is meant by the area enclosed by multiple polar curves?
An area enclosed by multiple polar curves could be
an area between two polar curves
an area partially enclosed by one polar curve and partially enclosed by another
How do I find the area enclosed by multiple polar curves?
STEP 1
If not given, a sketch, on the same diagram, of the curves is helpful
Identify any half-lines that are needed by looking for intersections between the curves
Identify any relevant values of θ such that r=0 (i.e. intersections with the pole)
This may involve solving equations in relevant ranges of θ
Look for symmetry to simplify the problemSTEP 2
Findfor both curves, manipulating them into integrable forms
This may involve using trigonometric identities and or common integration techniques such as reverse chain rule, ‘adjust and compensate’
Set up an integral for each partial area using the formula
STEP 3
Evaluate the integrals
Double/scale-up each integral as necessary if symmetry has been used
Total the partial integrals to find the entire area required
Examiner Tips and Tricks
Graph sketches do not have to be accurate, but should enable you to visualise the problem and get an idea of where intersections and half-lines are
Look out for when exact areas are required and whether your calculator can produce these using its integration function
Worked Example
A sketch of the polar curves defined by the following equations is shown below
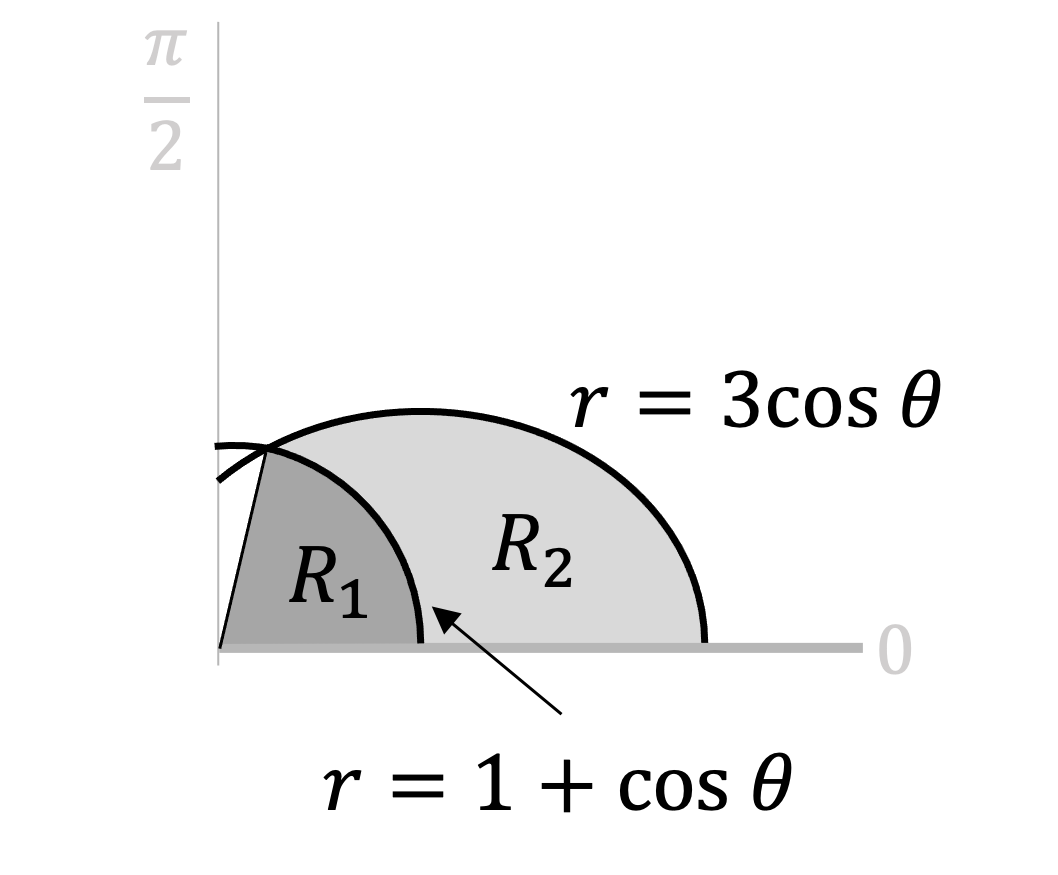
a) Find the area labelled .

a) Find the area labelled .


Unlock more, it's free!
Did this page help you?