Calculating Binomial Probabilities

Throughout this section we will use the random variable $X ~ B (n, p)$ . For binomial, the probability of a X taking a non-integer or negative value is always zero. Therefore any values mentioned in this section will be assumed to be non-negative integers.

Where does the formula for a binomial distribution come from?

The formula for calculating an individual binomial probability is
- $P (X = r) = p_{r} = (\begin{matrix} n \\ r \end{matrix}) p^{r} {(1 - p)}^{n - r}$
  - If there are r successes then there are $(n - r)$ failures
  - The number of times this can happen is calculated by the binomial coefficient
  - $(\begin{matrix} n \\ r \end{matrix}) = {}^{n}C_{r} = \frac{n!}{r! (n - r)!}$
This can be seen by considering a probability tree diagram with n trials, where p is the probability of success and the tree diagram is being used to find r successes
$(\begin{matrix} n \\ r \end{matrix})$ is the number of pathways through the tree there would be exactly r successes within the n trials
The formula allows statisticians to quickly find probabilities for larger values of n without needing to draw the whole tree diagram
Your calculator may have a function that would allow you to calculate binomial probabilities
- You can learn how to use this to check your work but it is important you always show your working using the formula to get the marks in the exam

How do I calculate the cumulative probabilities for a binomial distribution?

Most of the time you will be required to calculate cumulative binomial probabilities rather than individual ones
Use the formula to find the individual probabilities and then add them up
Make sure you are confident working with inequalities for discrete values
- Only integer values will be included so it is easiest to look at which integer values you should include within your calculation
- Sometimes it is quicker to find the probabilities that are not being asked for and subtract from one
$P (X \leq r)$ is asking you to find the probabilities of all values up to and including r
- This means all values that are at most r
- Don’t forget to include P(X = 0)
- It could also be written as $P (X \leq r) = 1 - P (X > r)$
$P (X < r)$ is asking you to find the probabilities of all values up to but not including r
- This means all values that are less than r
- Stop at r - 1
- It could also be written as $P (X < r) = 1 - P (X \geq r)$
$P (X \geq r)$ is asking you to find the probabilities of all values greater than and including r
- This means all values that are at least r
- It could also be written as $P (X \geq r) = 1 - P (X < r)$
$P (X > r)$ is asking you to find the probabilities of all values greater than but not including r
- This means all values that are more than r
- Start at r + 1
- It could also be written as $P (X > r) = 1 - P (X \leq r)$
If calculating $P (a \leq X \leq b)$ pay attention to whether the probability of a and b should be included in the calculation or not
- For example, $P (4 < X \leq 10)$ :
  - You want the integers 5 to 10

Worked example

If $X$ is the random variable $X ~ B (10, 0.35)$ . Find:

(i)

P (X = 3)

(ii)

P (X \leq 3)

(iii)

P (X > 3)

(iv)

P (3 < X < 6)

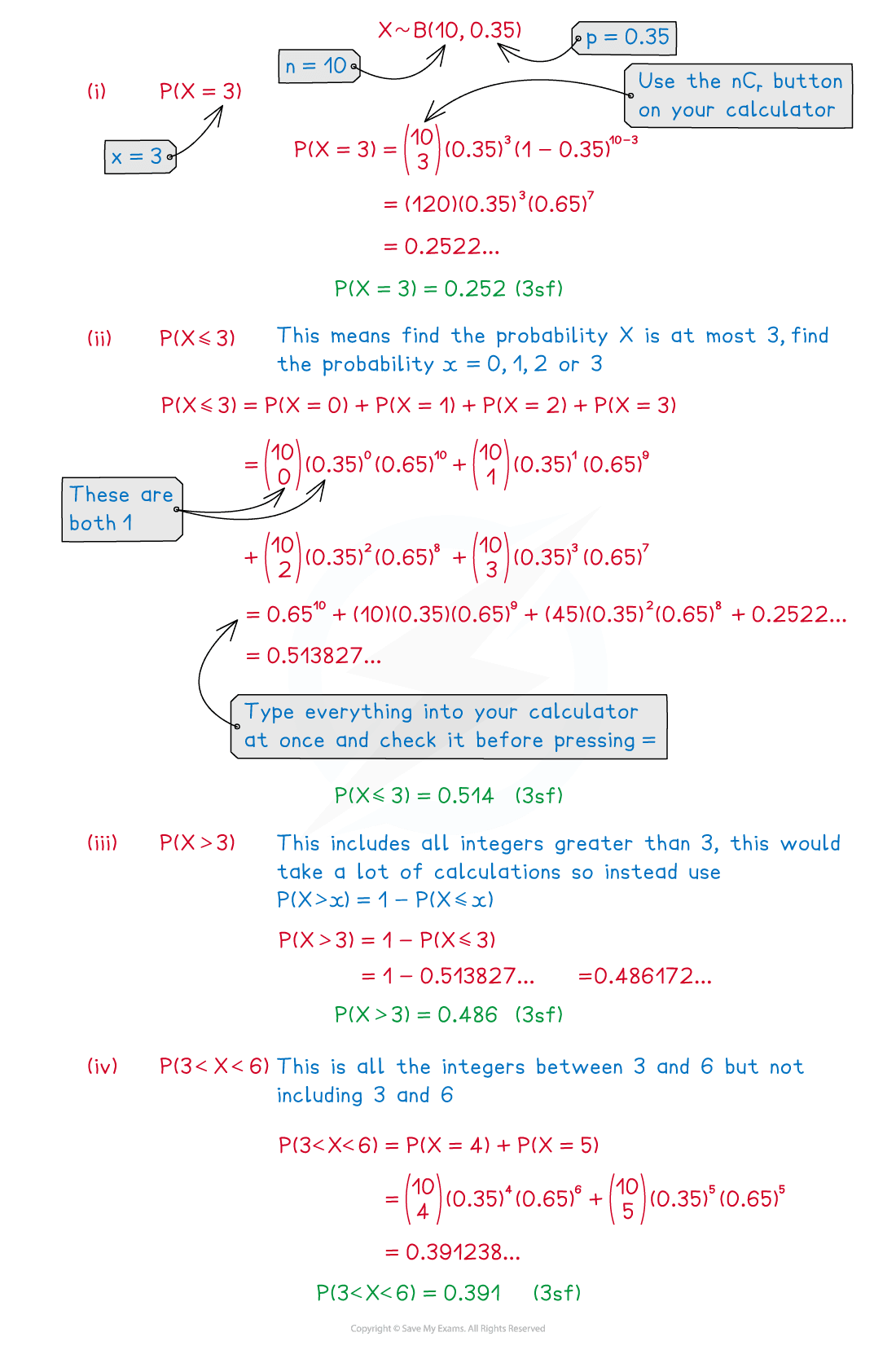
3-2-2-calculating-binomial-probabilities-we-solution

Examiner Tip

Looking carefully at the inequality within the probability is key here, make sure you consider which integers should be counted within your calculations.

Calculating Binomial Probabilities (CIE A Level Maths: Probability & Statistics 1)

Revision Note

Calculating Binomial Probabilities

Where does the formula for a binomial distribution come from?

How do I calculate the cumulative probabilities for a binomial distribution?

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Amber