Solving Equations with Modulus Functions (OCR A Level Maths A): Revision Note
Exam code: H240
Did this video help you?
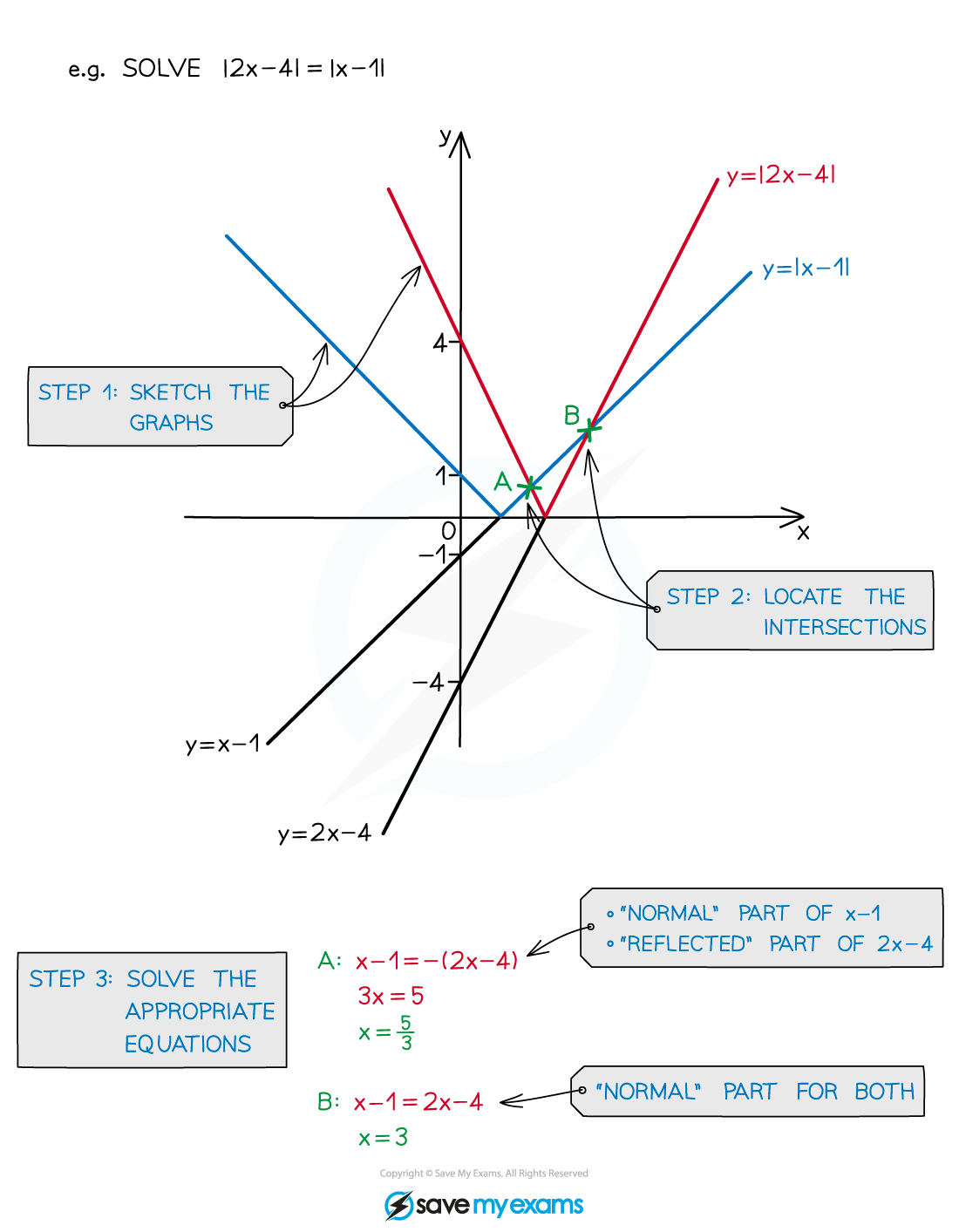
Solving equations with modulus functions
How do I sketch modulus equations?
Two non-parallel straight-line graphs would intersect once
If a modulus is involved there could be more than one intersection
Deducing where these intersections are is crucial to solving equations

How do I solve modulus equations?
STEP 1 Sketch the graphs including any modulus (reflected) parts
(see Modulus Functions – Sketching Graphs)
STEP 2 Locate the graph intersections
STEP 3 Solve the appropriate equation(s) or inequality
For
the two possible equations are
and
Examiner Tips and Tricks
Sketching the graphs is important as solving algebraically can lead to invalid solutions.
For example, x = 1 is a solution to
but it is not a solution to
(substitute x = 1 into both sides and see why it does not work).
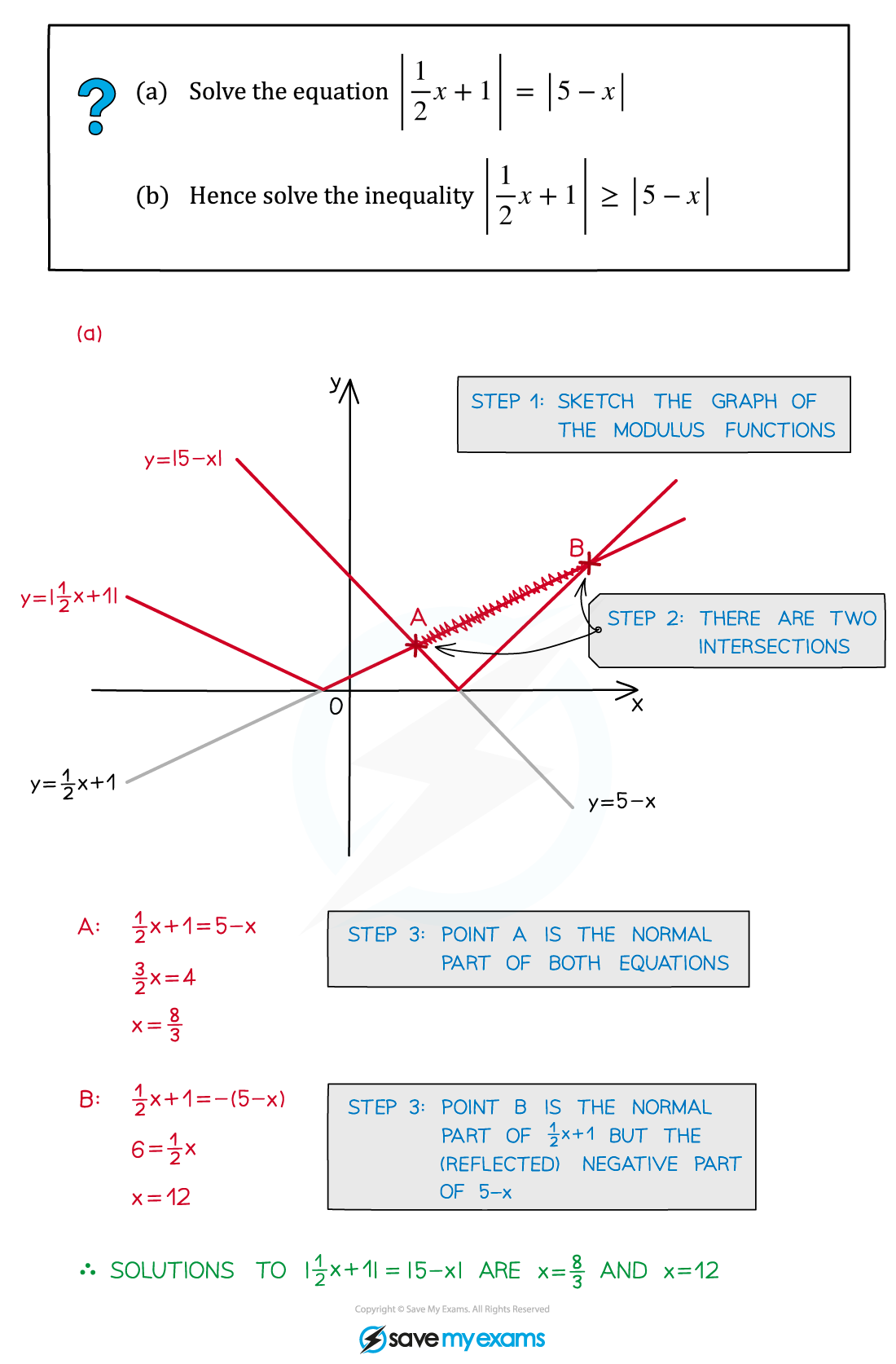
Worked Example


Unlock more, it's free!
Did this page help you?