Continuous Uniform Distribution (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Continuous Uniform Distribution
What is meant by the continuous uniform distribution?
This is a special case of a probability density function for a continuous random variable
The normal distribution is another special case covered in S1
The uniform, or rectangular, distribution is a p.d.f. that is constant and non-zero over a range of values but zero everywhere else
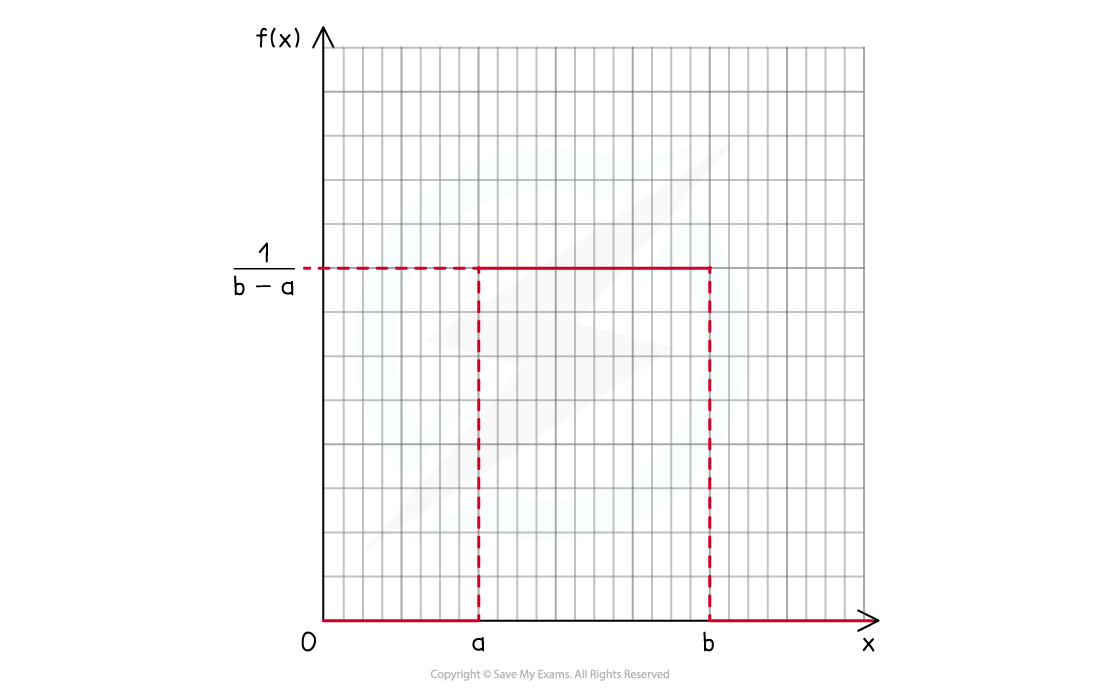
Since the area under the graph has to total 1, the height of the uniform distribution would be
Therefore the probability density function is given by
How do I find probabilities for a continuous uniform distribution?
Sketch the graph of y= f(x)
Probabilities are the area under the graph, all such areas will now be rectangles
Finding the area of a rectangle is likely to be easier than integration!
The symmetrical properties of rectangles may also be used to find probabilities
How do I find the mean, median, mode and variance of a continuous uniform distribution?
The mean, or expected value, is given by
This is the (vertical) axis of symmetry of the rectangle
Should the above be forgotten,
can still be applied
You be may asked to use this to prove the result
The median can also be found by symmetry and will be equal to the mean
There is no mode as f(x) is equal - and so at its greatest - for all values of x
The variance is given by
Should the above be forgotten,
or
can still be applied
You may be asked to use this to prove the result
The standard deviation is the square root of the variance
Worked Example
A continuous random variable, , is modelled by the uniform distribution such that
for
and
otherwise.
a is a constant.
(a) Show that the value of a is 1.5 .
(b) Find
(i)
(ii)
(c) Find the standard deviation of X, giving your answer in the form , where a is a rational number.

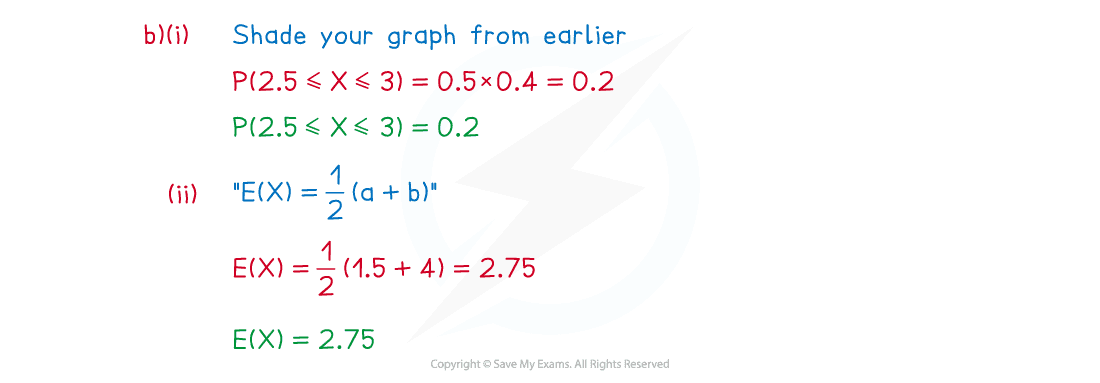

Examiner Tips and Tricks
A sketch of the graph of a uniform distribution is quick and will highlight the symmetry in a uniform distribution
Use areas of rectangles to find probabilities rather than integrating

Unlock more, it's free!
Did this page help you?