Exponential Growth & Decay (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note

Modelling Exponential Growth & Decay

What is exponential growth and decay?

• Exponential growth and exponential decay occur when the rate of change is proportional to the size of the variable itself

  • A population of rabbits will grow faster if there are more rabbits in total

  • A radioactive substance decays slower when there is less of the substance remaining

What is the equation for exponential growth or decay?

• Exponential growth and decay may be written in the forms:

  • 

  • 

    • Where are constants and is the exponential function

  • stretches the graph vertically by scale factor

  • determines the direction and rate of change

    • If it is an exponential growth

    • If it is an exponential decay

  • also determines the direction and rate of change

    • If it is an exponential growth

    • If it is an exponential decay

  • translates the graph vertically upwards by (after the vertical stretch)

  • The -intercept (when =0) for both forms will be equal to

• is an example of exponential growth

• is an example of exponential decay, as is negative

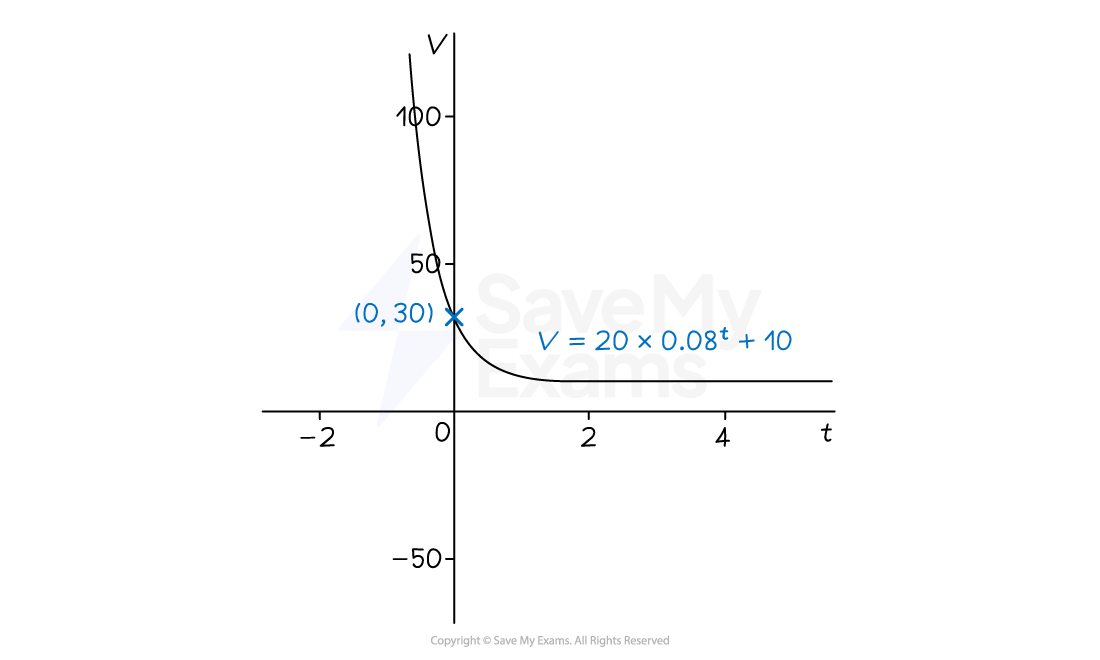
• is an example of exponential growth

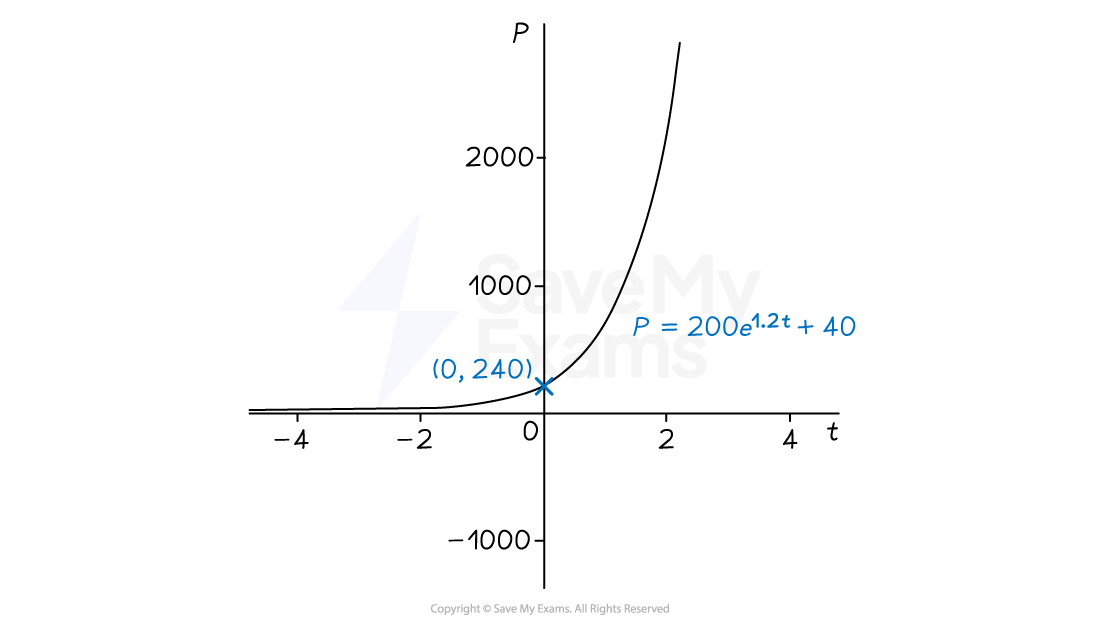
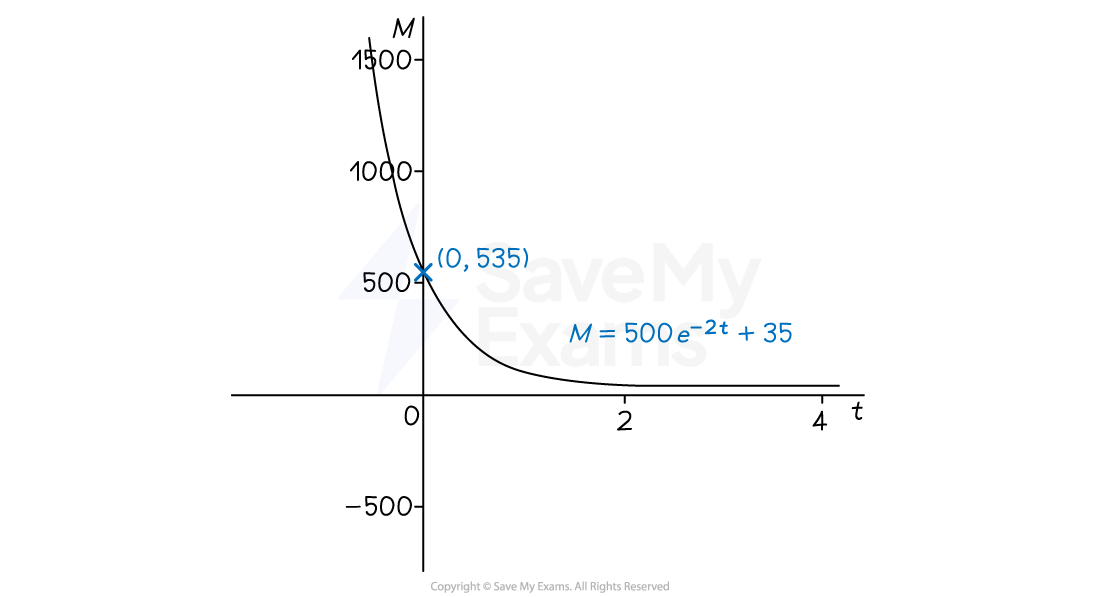
• is an example of exponential decay, as is negative

• You may also see equations of exponential growth and decay written in a factorised form

  • E.g. could be written as

What can an exponential model be used for?

• Similar to other types of graphical model, exponential models can be used to estimate or predict data points that are not known

  • The graph and model can be used to interpolate values that were not directly measured from the scenario

  • Remember that interpolation has a much greater validity than extrapolation

  • Extrapolating exponential functions can lead to large errors as they can increase (or decrease) very rapidly

• Predicted values can be found by substituting in the relevant known quantity

  • E.g. Substituting in a time to find a mass

• When finding an unknown power, you may need to use logarithms to do this

  • E.g. When substituting in a mass to find a time

What is a half-life?

• In an exponential decay, the half-life is the time taken the for value of a function to halve

• The half-life is constant throughout the decay

  • E.g. For a decaying substance,

    • The time taken to decay from 100 grams to 50 grams,

    • is exactly the same as the time taken to decay from 50 grams to 25 grams