Revision NotesPast Papers
International A Level (IAL)Further MathsEdexcelFurther Pure 1Revision NotesCoordinate SystemsCoordinate SystemsThe Parabola

The Parabola (Edexcel International A Level (IAL) Further Maths) : Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

The Equation of a Parabola

What is a parabola?

  • A parabola is a U-shaped quadratic curve with a line of symmetry

    • y equals x squared is a parabola

      • The line of symmetry is the y-axis

    • x equals y squared is a parabola

      • The line of symmetry is the x-axis

  • A parabola is part of a family of curves called the conics (or conic sections)

    • Conics are parabolae, hyperbolae and ellipses

What is the general equation of a parabola?

The general parabola
The general parabola

  • The general equation for a parabola is

    • y squared equals 4 a x in Cartesian form

    • x equals a t squared comma space space y equals 2 a t in Parametric form

      • where a is a positive constant

  • The x-axis is the line of symmetry, as shown

  • The general equation can be rearranged

    • y equals plus-or-minus square root of 4 a x end root

      • y equals square root of 4 a x end root is the branch above the x-axis

      • y equals negative square root of 4 a x end root is the branch below the x-axis

Examiner Tips and Tricks

You are given the Cartesian and parametric equations of a parabola in the Formulae Booklet.

Worked Example

A parabola has the parametric equations x equals a t squared and y equals 2 a t where a greater than 0.

Show that its Cartesian equation is y squared equals 4 a x.

To find the Cartesian equation, eliminate t from the parametric equations
It is easier to make t the subject of y equals 2 a t

t equals fraction numerator y over denominator 2 a end fraction

Substitute this into the equation for x and simplify

table row x equals cell a open parentheses fraction numerator y over denominator 2 a end fraction close parentheses squared end cell row x equals cell fraction numerator a y squared over denominator 4 a squared end fraction end cell row x equals cell fraction numerator y squared over denominator 4 a end fraction end cell end table

Make y squared the subject

y squared equals 4 a x

The Focus & Directrix of a Parabola

What are the focus and directrix of a parabola?

  • The focus of the parabola y squared equals 4 a x is the point  open parentheses a comma space 0 close parentheses on the x-axis

  • The directrix is the vertical line x equals negative a

  • For example, the parabola y squared equals 12 x where a equals 3 has

    • a focus at open parentheses 3 comma space 0 close parentheses

    • the directrix x equals negative 3

What is the focus-directrix property?

  • The focus-directrix property says that:

    • “Points on a parabola are the same distance from the focus as they are horizontally from the directrix”

  • In other words:

    • If S is the focus of a parabola

    • and P is any point on the parabola

    • and X is the point on the directrix horizontally from P

    • Then the distance PS equals PX

      • PS = PX

  • This property is an example of a locus of points

Examiner Tips and Tricks

You are given the focus and directrix of a parabola in the Formulae Booklet, but not the focus-directrix property.

Worked Example

The diagram shows the point S open parentheses a comma 0 close parentheses, the vertical line x equals negative a and a general point P open parentheses x comma y close parentheses that can move in the plane.

The focus S, directrix x=-a and a general point P

If P is restricted to always be the same distance from S as it is horizontally from the vertical line, use coordinate geometry to prove that it must lie on the parabola y squared equals 4 a x.

It helps to add the point X on to the diagram, on the line x equals negative a  horizontally from P
The question says that PS  = PX
The distance PS  can be found using Pythagoras' theorem 

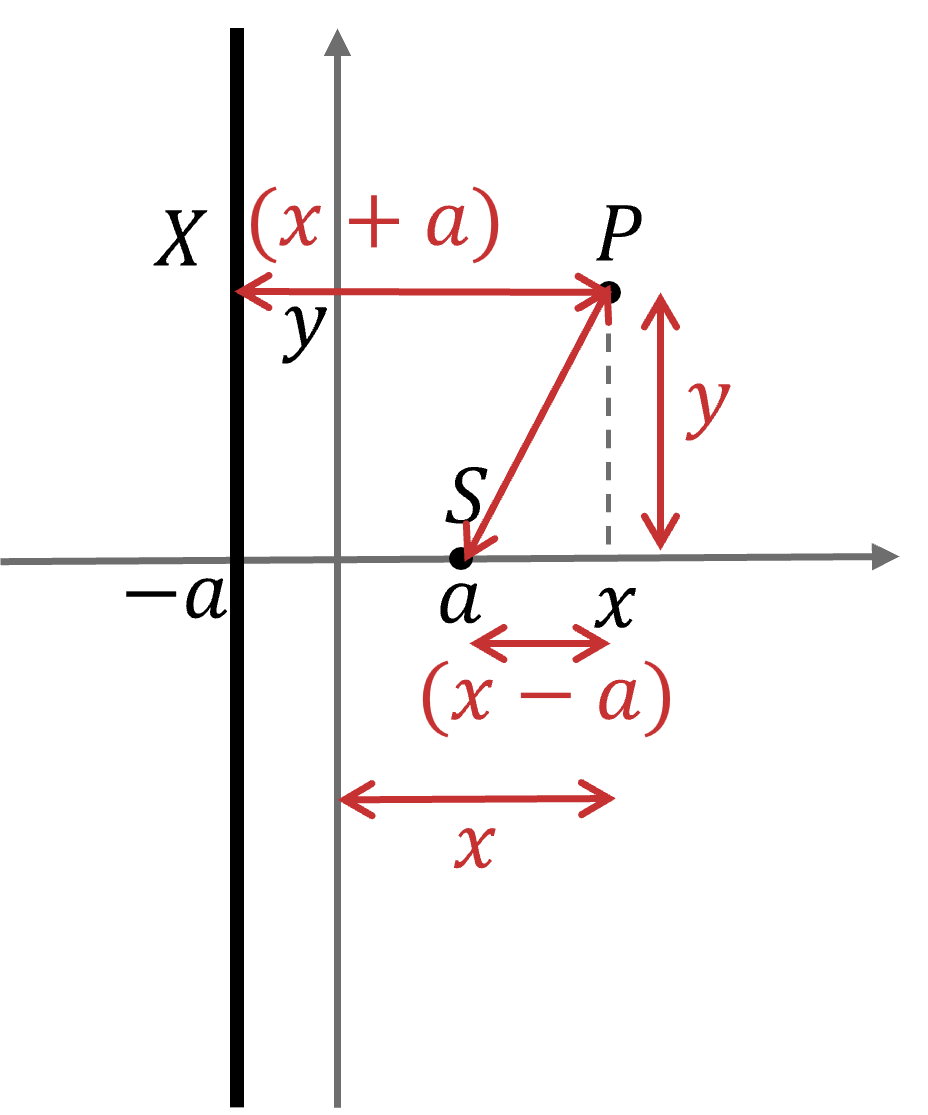
Using the focus-directrix property to prove its a parabola

P S squared equals open parentheses x minus a close parentheses squared plus y squared

The distance PX  can be found from the diagram

P X equals x plus a

Square PS  = PX  and substitute in the results above

table row cell P S squared end cell equals cell P X squared end cell row cell open parentheses x minus a close parentheses squared plus y squared end cell equals cell open parentheses x plus a close parentheses squared end cell end table

Expand and simplify both sides

table row cell x squared minus 2 a x plus a squared plus y squared end cell equals cell x squared plus 2 a x plus a squared end cell row cell negative 2 a x plus y squared end cell equals cell 2 a x end cell row cell y squared end cell equals cell 4 a x end cell end table

P open parentheses x comma space y close parentheses must lie on this curve

y squared equals 4 a x

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Newton-Raphson MethodNext:The Rectangular Hyperbola
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.