Composite Functions (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Did this video help you?
Composite functions
What is a composite function?
A composite function is where one function is applied after another function

The ‘output’ of one function will be the ‘input’ of the next one
Sometimes called function-of-a-function
A composite function can be denoted
All of these mean “
of
”

How do I use composite functions?

Recognise the notation
fg(x) means “f of g of x”
The order matters
First apply g to x to get
Then apply f to the previous output to get
Always start with the function closest to the variable
is not usually equal to
What are special cases of composite functions?

fg(x) and gf(x) are generally different but can sometimes be the same
ff(x) is written as f2(x)
Inverse functions ff-1(x) = f-1f(x) = x
Examiner Tips and Tricks
Domain and range are important.In fg(x), the ‘output’ (range) of g must be in the domain of f(x), so fg(x) could exist, but gf(x) may not (or not for some values of x).
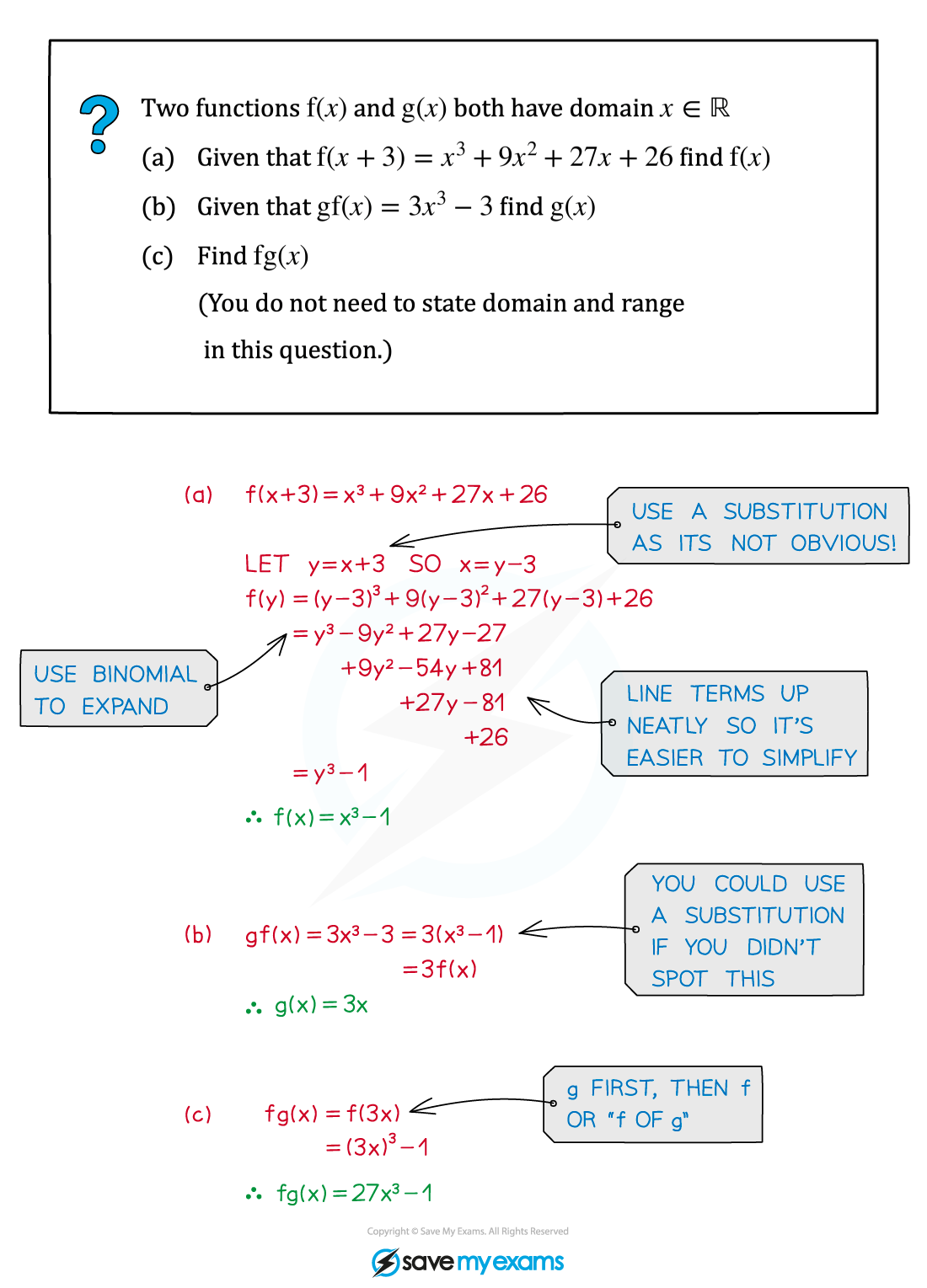
Worked Example

Unlock more, it's free!
Did this page help you?