Sketching Graphs of Modulus Functions (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Did this video help you?
Sketching graphs of modulus functions
What is the modulus function?
The modulus function makes any ‘input’ positive
|x| = x if x ≥ 0 |f(x)| = f(x) if f(x) ≥ 0
|x| = -x if x < 0 |f(x)| = -f(x) if f(x) < 0
For example: |5| = 5 and |-5| = 5
Sometimes called absolute value
How do I sketch the straight line modulus graph y = a|x+p|+q?
The graph will look like a “ꓦ” if a > 0 or a “ꓥ” if a < 0
There will be a vertex at the point (-p, q)
There could be 0, 1 or 2 roots
This depends on the location of the vertex and the orientation of the graph (ꓦ or ꓥ)
Compare this to the completed square form of a quadratic a(x + p)² + q
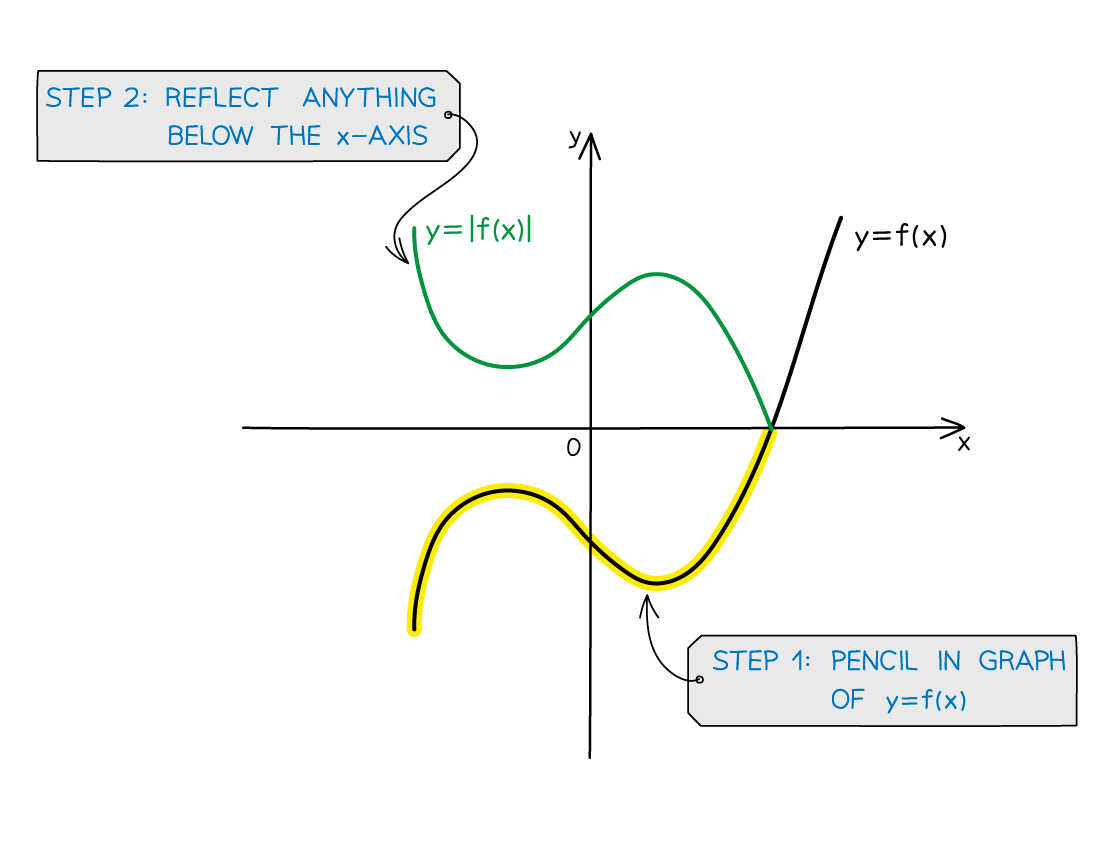
How do I sketch the modulus of a function y = |f(x)|?
STEP 1 Pencil in the graph of y = f(x)
STEP 2 Reflect anything below the x-axis, in the x-axis, to get y = |f(x)|
How do I sketch functions of mod x, y = f(|x|)?
STEP 1 Sketch the graph of y = f(x) only for x ≥ 0
STEP 2 Reflect this in the y-axis

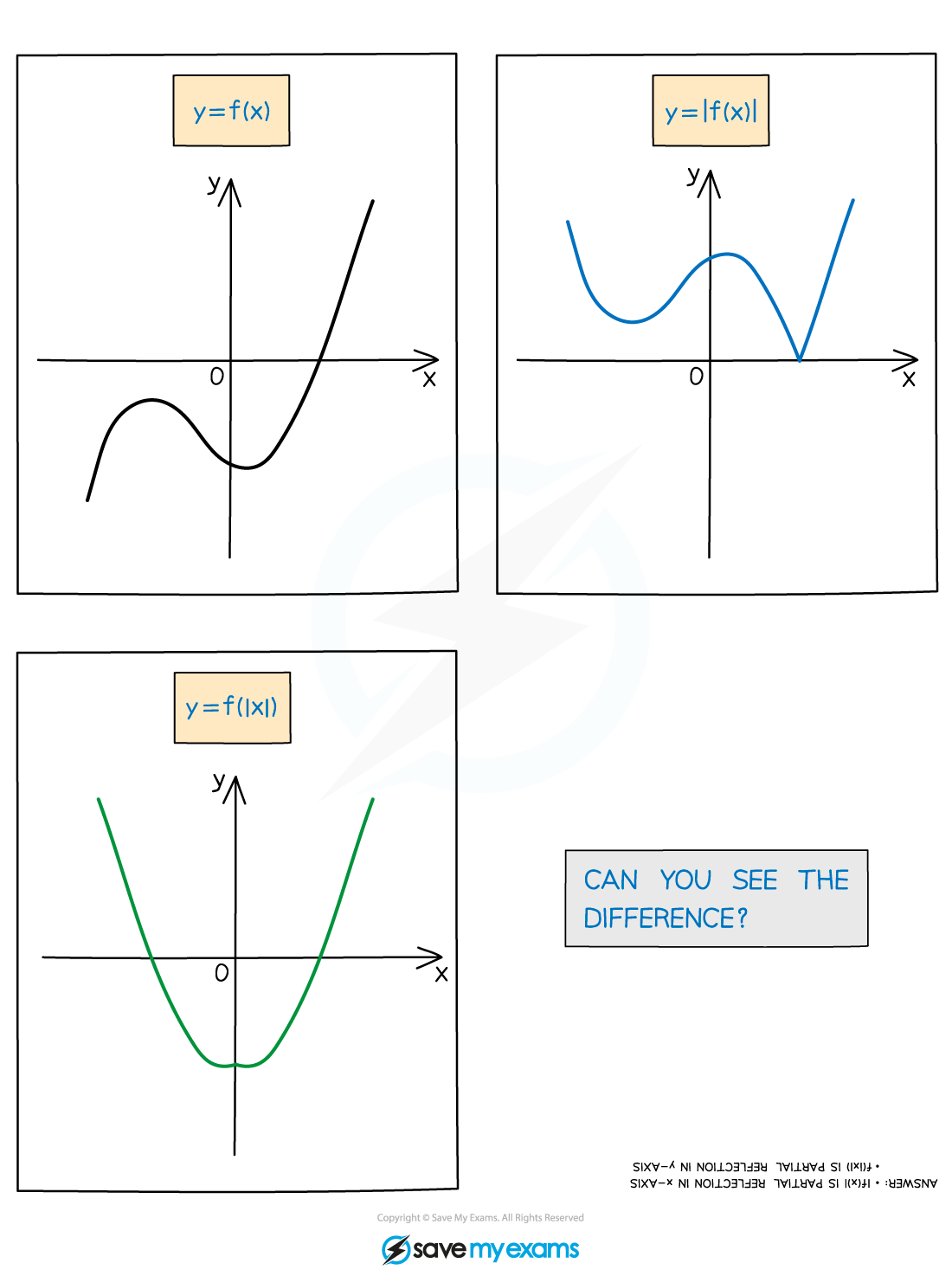
What is the difference between y = |f(x)| and y = f(|x|)?
There is a difference between y = |f(x)| and y = f(|x|)
The graph of y = |f(x)| never goes below the x-axis
It does not have to have any lines of symmetry
The graph of y = f(|x|) is always symmetrical about the y-axis
It can go below the y-axis
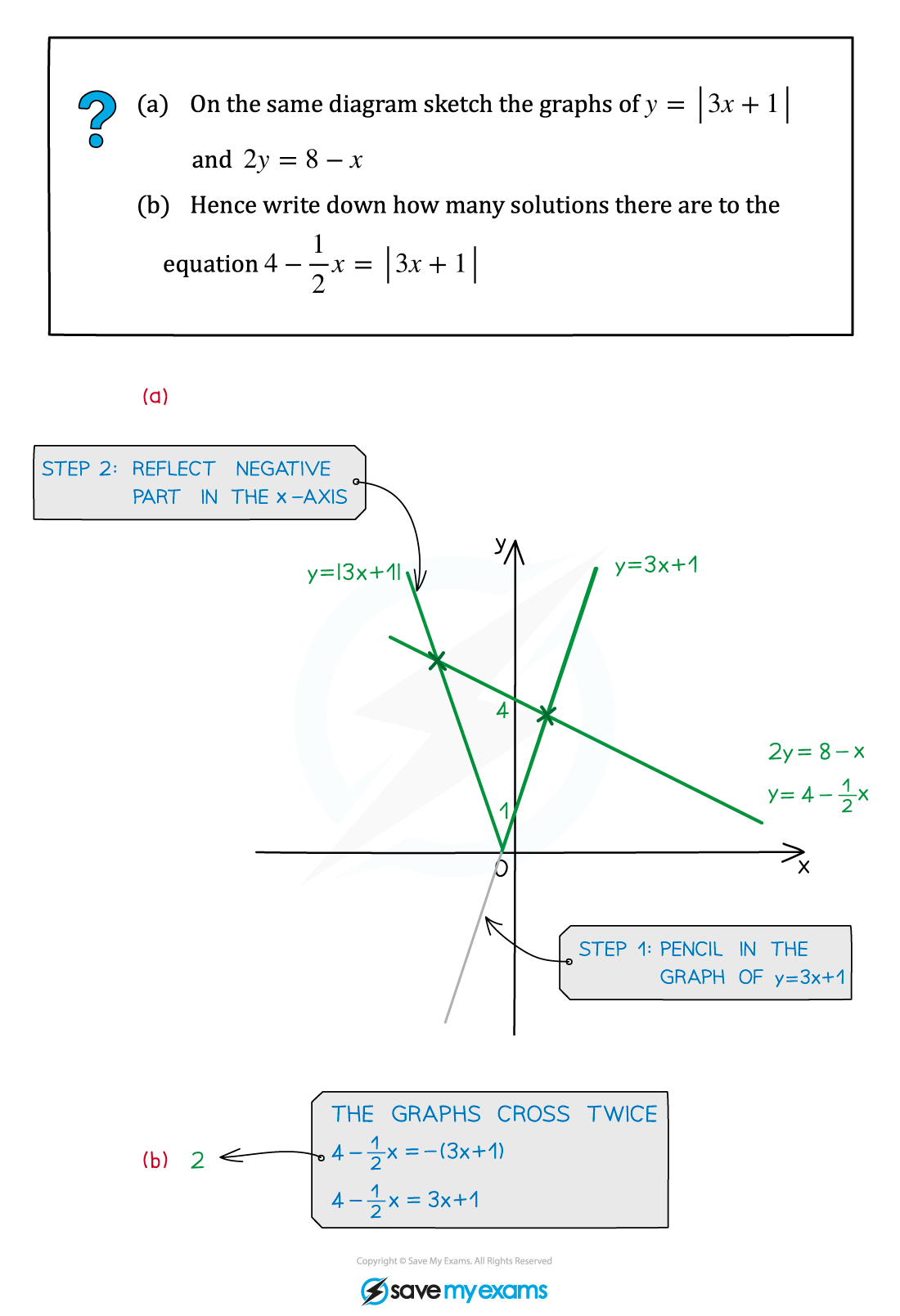
Worked Example

Unlock more, it's free!
Did this page help you?