Sorting Algorithms (Edexcel International AS Maths): Revision Note
Exam code: XMA01
Introduction to Sorting Algorithms
Sorting algorithms arrange items into ascending or descending order
Items that are usually sorted include values, letters or words
As a list of items becomes larger, it becomes increasingly difficult for a human to sort
A computer can be programmed with a sorting algorithm
This makes the process both accurate and efficient
With sorting algorithms in particular, it is important to stay in 'robot mode'
Follow each step of the algorithm precisely, in order, exactly as a robot would
Do not be tempted to take shortcuts or miss parts of the algorithm out because the answer can be 'seen'
Bubble Sort
What is the bubble sort algorithm?
The bubble sort algorithm arranges items into either ascending or descending order
Items are usually values
They could also be letters or words or similar
For questions given in context, values will be measures such as weights, lengths, scores or times
How does the bubble sort algorithm work?
Bubble sort works by comparing pairs of items on the working list
Comparisons are made working from left to right
The first item is compared to the second, the second to the third, and so on
A swap occurs if a pair of items are not in order
A pair of equal items does not count as a swap
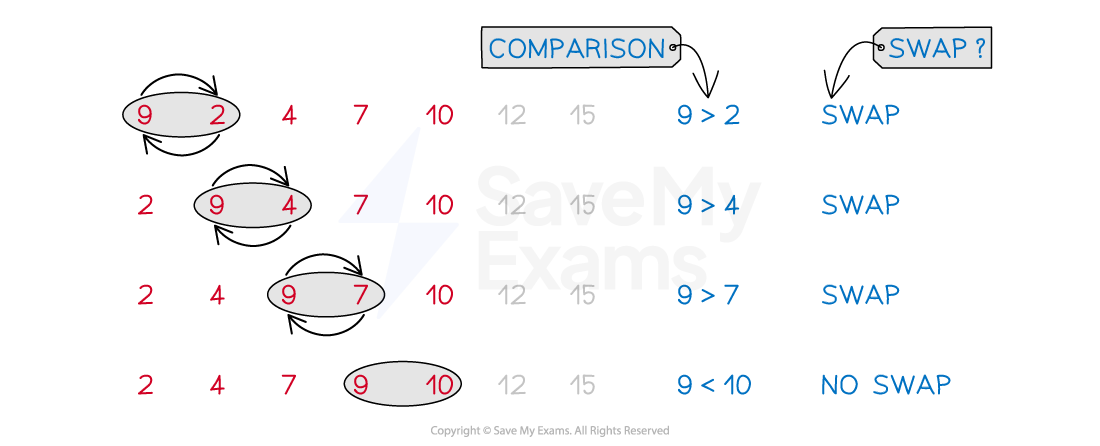
This comparison of pairs and swaps continues until the end of the working list is reached
This is called a pass
Several passes are usually required to order a list of items
At the end of each pass, the item at the end of the working list is in the correct place
For ascending order, the highest value 'bubbles' to the end
Bubble sort, for
items, is complete when either
a pass involves no swaps, or
after the
pass
I.e. when only one item would remain on the working list
What is the working list?
The working list is the list of unordered items that a pass of the bubble sort algorithm will apply to
For the first pass every item on the list is in the working list
After the first pass, the final item is in the correct place
This item is removed from the working list
You may 'see' that other items are in the correct places
However, the algorithm ensures the highest (or smallest) item is at the end of the list
The working list is reduced by one after each pass
This keeps the bubble sort as efficient as possible by not requiring unnecessary comparisons
For a list of
items
The first pass will have
items on the working list
The second pass will have
items on the working list
(If required) the
pass will have 2 items on the working list
The ordered items may be described as the sorted list
The image below shows a list at the end of the second pass of an ascending bubble sort
Two items are on the sorted list (12 and 15)
The 10 being in the correct position is irrelevant at this stage
The third pass will confirm the position of the 10 and it will become part of the sorted list

How do I work out the (maximum) number of passes in the bubble sort algorithm?
For a list of
items
The maximum number of passes will be
After the
pass,
items will be in order
The last remaining item must be in order too
It is hard to predict how many passes the bubble sort will need
It may be possible to tell how many more passes are required when only a few items are out of order
If the item at the end of the list should be at the start then it will take
passes
This is because this item will only move one space closer to the start after each pass
How do I work out the (maximum) number of comparisons in the bubble sort algorithm?
For a list of
items
The number of comparisons at each pass will always be one less than the number of items on the working list
The first pass will have
items on the working list so there will be
comparisons
The second pass will have
comparisons
The
pass will have
comparisons
(If required) the
pass will have 1 comparison
The maximum number of comparisons for the entire bubble sort algorithm would be
or
Understanding the logic for the number of comparisons is easier than trying to remember a formula
How do I work out the (maximum) number of swaps in the bubble sort algorithm?
For a list of
items
The maximum number of swaps in a pass would be the same as the number of comparisons for that pass
I.e. if every comparison results in a swap being made
This would occur if the first item on the working list is the largest (or smallest for descending)
With a small working list it is possible to 'see' or count the number of swaps required for a pass
For a longer list, keep a tally of swaps as you perform a pass
The maximum number of swaps for the entire algorithm would be needed if a list started in reverse order
Examiner Tips and Tricks
Make it clear when you have completed the bubble sort algorithm
State how you know it is complete
E.g. "There were no swaps in the fifth pass so the algorithm is complete and the list is in order"
After completing your solution, check again if the list should be in ascending or descending order
If you've got it the wrong way round, there's no need to redo the question but
Make it clear that after the algorithm is completed, you are reversing the list
Make sure your final answer is in the order required by the question
Worked Example
The times, to the nearest second, taken by 7 participants to answer a general knowledge question are 5, 7, 4, 9, 3, 5, 6.
The times are to be sorted into ascending order using the bubble sort algorithm.
a) Write down
i) the maximum number of passes the algorithm will require,
ii) the number of comparisons required for the third pass,
iii) the number of swaps there will be in the first pass.
i) The maximum number of passes is
The maximum number of passes will be 6
ii) The pass will have
comparisons
The number of comparisons required in the third pass will be 4
iii) Carefully do this by inspection (or you can carry out the first pass to be sure but that takes time)
The first swap will be the 7 and 4
The 9, being the highest value on the list, will then swap with each of the values that follow it (3 values)
The number of swaps in the first pass is 4
b) After the second pass of the bubble sort algorithm, the times are in the order 4, 5, 3, 5, 6, 7, 9.
Perform the third pass of the bubble sort algorithm and state the number of swaps made.
As this is the third pass, the last two items on the list, 7 and 9, will already be in the correct place
The working list (that we apply a pass of the bubble sort algorithm to) will be 4, 5, 3, 5, 6
4 | 5 | 3 | 5 | 6 | 7 | 9 |
| 4 < 5, no swap |
4 | 5 | 3 | 5 | 6 | 7 | 9 |
| 5 > 3, swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| 5 = 5, no swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| 5 < 6, no swap |
4 | 3 | 5 | 5 | 6 | 7 | 9 |
| end of pass 3 |
Number of swaps: 1
c) Explain why two further passes of the bubble sort algorithm are required to ensure the list is in ascending order.
At this stage of the algorithm you should be able to deduce the answer by inspection of the current list
Using the answer to part (b), the current list is 4, 3, 5, 5, 6, 7, 9
The next pass will involve one swap - the 4 and the 3
The pass after that will involve no swaps and so the algorithm will be complete and the list will be in order
Thus, two further passes are required
It is important to state that the algorithm is complete and the reason why
Quick Sort
What is the quick sort algorithm?
The quick sort algorithm arranges items into either ascending or descending order
Items are usually values
They could be letters or words or similar
For questions given in context values will be measures such as weights, lengths, scores or times
How does the quick sort algorithm work?
Each pass of the quick sort algorithm works by splitting a sub-list of the items into two halves around a pivot
One half will be the sub-list of values that are less than the pivot
For ascending order this sub-list would come before the pivot
The other half will be the sub-list of values that are greater than the pivot
For ascending order this sub-list would come after the pivot
Values that are equal to the pivot can be listed in either half
But for consistency always list items equal to the pivot in the half greater than the pivot
On both sides of the pivot, values should be listed in the order they appear in the original list
The algorithm is complete when every item on the (original) list has been designated as a pivot
Which item is the pivot in the quick sort algorithm?
The pivot is the middle value in a sub-list of the items, without reordering
For a list containing
items, the pivot will be the
th item
For consistency round up if necessary
In the first pass, there will be one pivot
This is the middle item in the whole list
In the second pass, there could be two (new) pivots
One pivot in the lower sub-list and one in the upper sub-list
The number of pivots could double at each pass
But this will not always be the case
If a pivot is the lowest or greatest item on a sub-list
How do I apply the quick sort algorithm?
The following list of steps describes the quick sort algorithm for arranging a list of items into ascending order
Arranging into descending order would be the same
However, the 'ordering' in Step 2 would be reversed
STEP 1
Find and highlight the pivot (middle value) for each sub-list of itemsFor the first pass only, the sub-list will be the same as the entire list of items
STEP 2
List items lower than the pivot, in the order they appear, before the pivot
Then write the pivot as the next number on the listList items greater than or equal to the pivot, in the order they appear, after the pivot
STEP 3
Repeat steps 1 and 2 until every item on the original list has been designated a pivot
The original (full) list of items will now be in ascending order
Examiner Tips and Tricks
Make it clear which items you have chosen as pivots at each pass of the quick sort algorithm
Use different styles to highlight the pivots such as
underlining values using solid, dotted, wavy, double lines etc.
drawing different shaped boxes (e.g. rectangle, circle, star) around values
Do not use different colours on the exam paper as they may not show up on the examiner's scanned copy
Worked Example
The following values are to be sorted into descending order using the quick sort algorithm.
5, 3, 7, 2, 4, 5, 9, 6
Clearly showing your choice of pivots at each pass, perform the quick sort algorithm to sort the list into descending order.
STEP 1
This is the first pass so the entire list will be the sub-listThere are 8 values so the pivot will be the
rounded up to the 5th value on the list
Pass 1 (pivot 4)
5 | 3 | 7 | 2 | 5 | 9 | 6 |
STEP 2
As descending order is required, list items greater than the pivot (4) before it; items lower than the pivot after it
Keep the numbers in the order they are already in
5 | 7 | 5 | 9 | 6 | 3 | 2 |
STEP 3
There are now two sub-lists 5, 7, 5, 9, 6 and 3, 2
Repeat steps 1 and 2 on these sub-lists
Pass 2 (pivots 5 and 2)
5 | 7 | 9 | 6 | 3 |
The (repeated) 5 will go into the 'greater than or equal to' sub-list (before the pivot 5 as descending)
There will be no new sub-lists at the next pass after the pivot 5 or pivot 2 as they are the lowest values in their current sub-lists
5 | 7 | 9 | 6 | 3 |
Continuing repeating steps 1 and 2 on each new sub-list until every item has been designated a pivot
Pass 3 (pivots 9 and 3)
5 | 7 | 6 |
5 | 7 | 6 |
Pass 4 (pivot 7)
5 | 6 |
5 | 6 |
Pass 5 (pivot 6)
5 |
5 |
Pass 6 (pivot 5)
Every value has now been designated as a pivot so the algorithm is complete and the list is in descending order
9, 7, 6, 5, 5, 4, 3, 2

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?