Critical Paths (Edexcel International AS Maths): Revision Note
Exam code: XMA01
Introduction to Critical Path Analysis
What is critical path analysis?
Critical path analysis (CPA) is the use of an activity network for a project that determines
The minimum duration of the entire project
The critical activities
These are the activities that must start and finish at the earliest possible time so that the project can be completed in its minimum duration
The critical path
The path from the source node to the sink node that encompasses all the critical activities
In harder problems there may be more than one critical path
Any possible delay to starting non-critical activities
The total float of an activity is the time it can be delayed by as to not affect the minimum project duration
Earliest Event Times
What are earliest (or early) event times?
The earliest event time is the earliest time at which an activity can commence from its starting event
This will determine the minimum project duration
On an activity network, each event (node) will have two boxes that require completing
Sometimes the boxes will replace the circled event (node) number
Sometimes the boxes will be drawn next to the circled event (node) number
The top box will be the earliest event time
The bottom box is for the latest event time (see the next section of this revision note)
The earliest event times must be completed before the latest event times

How do I work out early event times?
Starting at the source node, this will be 0
This is the starting point of the project, i.e. time zero
Working forwards from the source node, look at each of the activities (arcs) leading to an event (node)
For each preceding activity of an event (node)
Add the early event time from that activity's start node to its duration
The earliest event time is then the maximum of these times
This is the earliest time an event can be moved on from

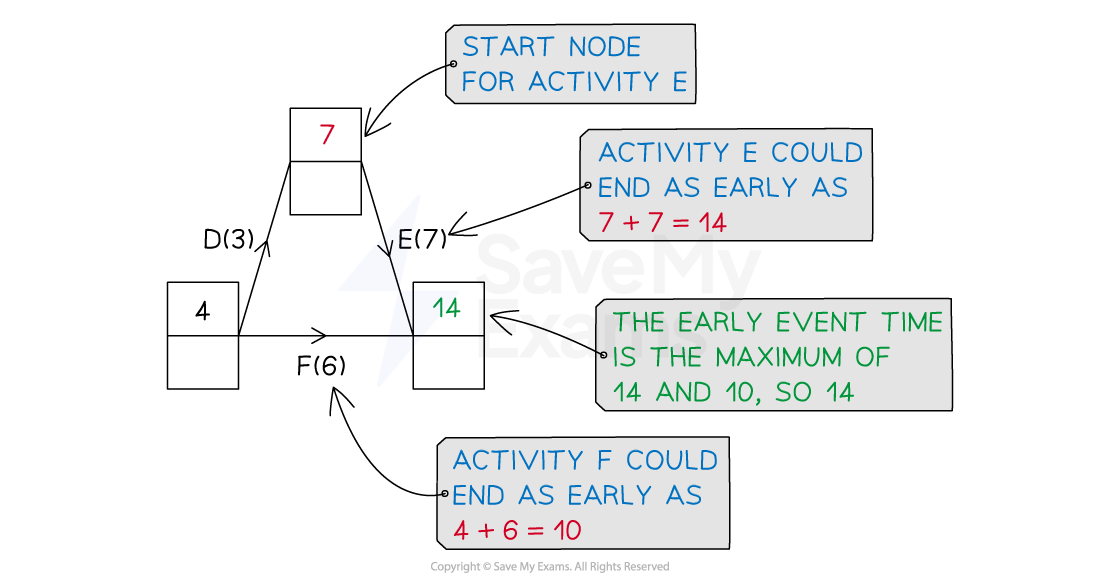
Completing the earliest event times is sometimes referred to as a forwards pass (through the activity network)
Examiner Tips and Tricks
An 'early event time' is the 'latest time' leading to a node !
Ensure you check all arcs leading to a node
Be particularly careful with dummies (they still count) as these are unlabelled with a duration of 0
Worked Example
Complete the early event times for the activity network given below.
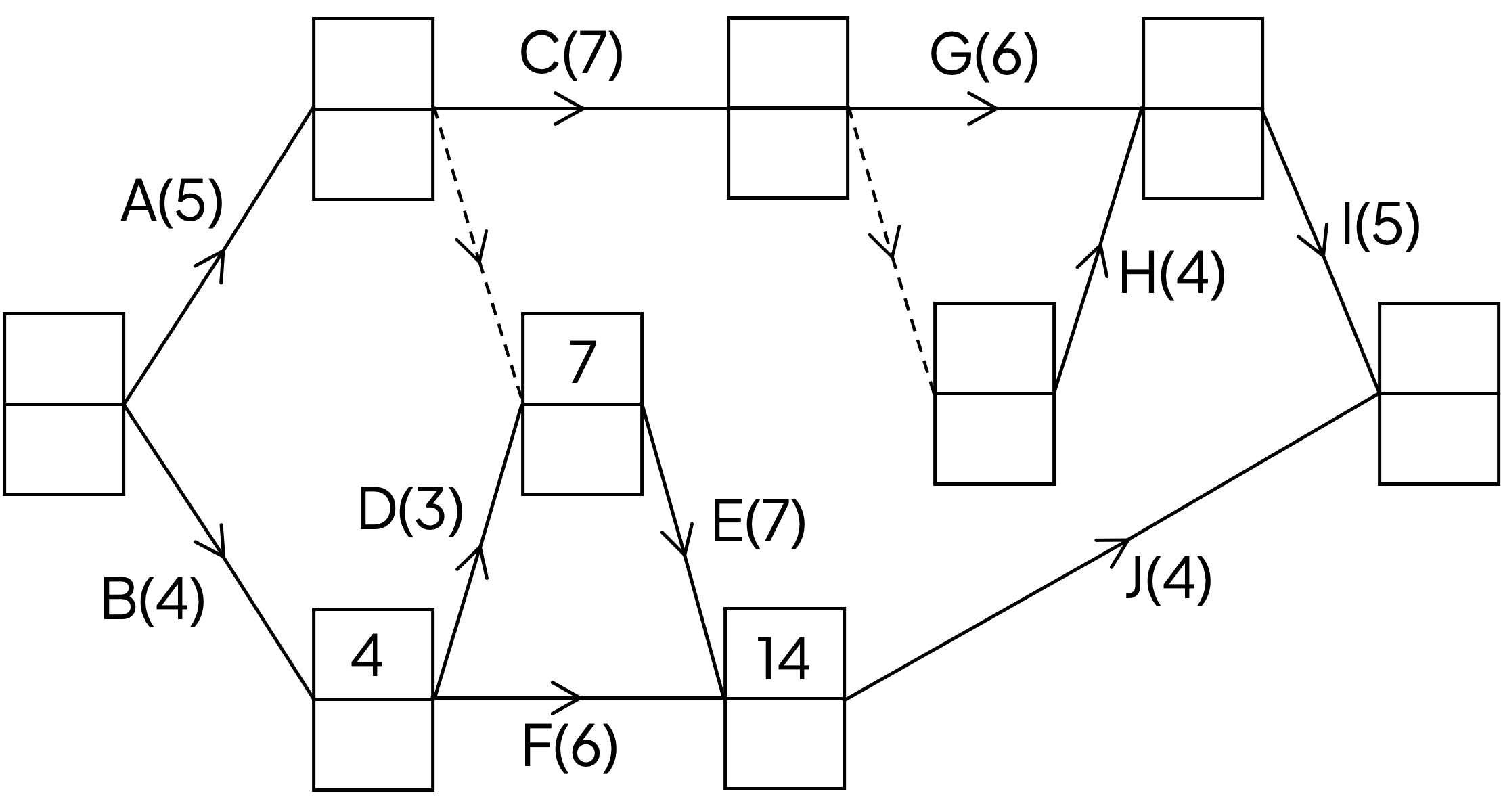
Early event times go in the top box at each node
Three of the earliest times are completed, so we just need to work along the top of the diagram
Start at the source node with early event time 0
Only activity A leads to the event (node) at the end of activity A
Similarly for activity C
(The earliest event time at the start of C is 5)
A dummy activity has a duration of 0, so the early event time at the end of the after C will also be 12
Activities G and H lead to the same event
Finally both activities I and J lead to the sink node
Complete the early event times on the network

Latest Event Times
What are latest (or late) event times?
The latest event time is the latest time at which an activity can commence from its starting event
without affecting the minimum project duration
On an activity network, each event/node will have two boxes that require completing
Sometimes the boxes will replace the circled event/node number
Sometimes the boxes will be drawn near to the circled event/node number
The bottom box will be the latest event time

The top box is for the earliest event time (see the previous section of this revision note)
The earliest event times must have been completed before the latest event times
How do I work out late event times?
Starting at the sink node, this will be the same as the early event time
This is the minimum duration of the project
I.e. The shortest time in which all activities can be completed
Working backwards from the sink node, look at each of the activities (arcs) leading back to an event (node)
For each activity after an event (node)
Subtract that activity's duration from the latest event time at its end node
The latest event time is then the minimum of these times
This is the latest time an event can be moved on from such that all activities can be completed in the minimum duration of the project

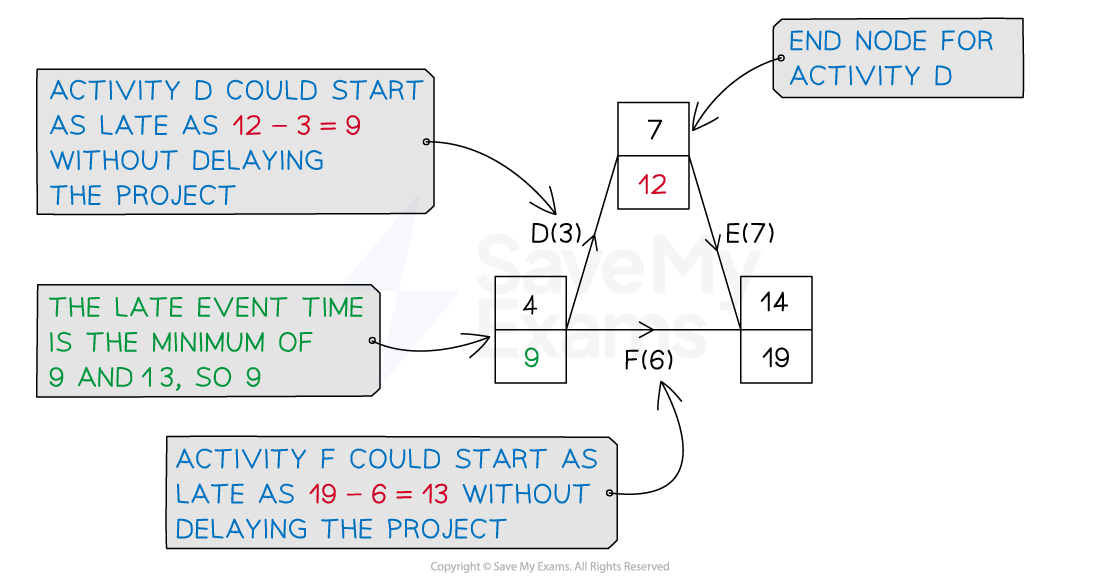
Completing the latest event times is sometimes referred to as a backwards pass (through the activity network)
Worked Example
Complete the late event times for the activity network given below.

Late event times go in the bottom box at each node
Three of the latest times are completed, so we just need to work along the top of the diagram
Start at the sink node
Its latest time will be the same as its earliest time, 23
Only activity I leads back to the event/node at the start of activity I
Similarly for activity H
(The latest event time at the end of H is 18)
Activities G and a dummy lead back to an event
Activities C and a dummy lead back to an event
Finally the source node
Complete the late event times on the network

Total Float of an Activity
What is the total float of an activity?
The total float of an activity is the time the start of an activity can be delayed
without affecting the minimum project duration
Critical activities will have zero float
How do I work out the total float of an activity?
For non-critical activities the total float can be calculated
Consider the earliest time it can commence and the latest time it can finish
In words

Formally, you may see this written as
The total float,
, of activity
, is defined to be
where
is the earliest time for event
and
is the latest time for event
Do not be put off by the word 'total'
The total float of an activity is one value for one activity!
Examiner Tips and Tricks
In many cases, the total float can just be 'seen' or thought about by considering the activity network
Where things are complicated or busy, it is best to think about the formal way of calculating them
Worked Example
The activity network below shows the duration of activities A-J and the early and late times at each event.
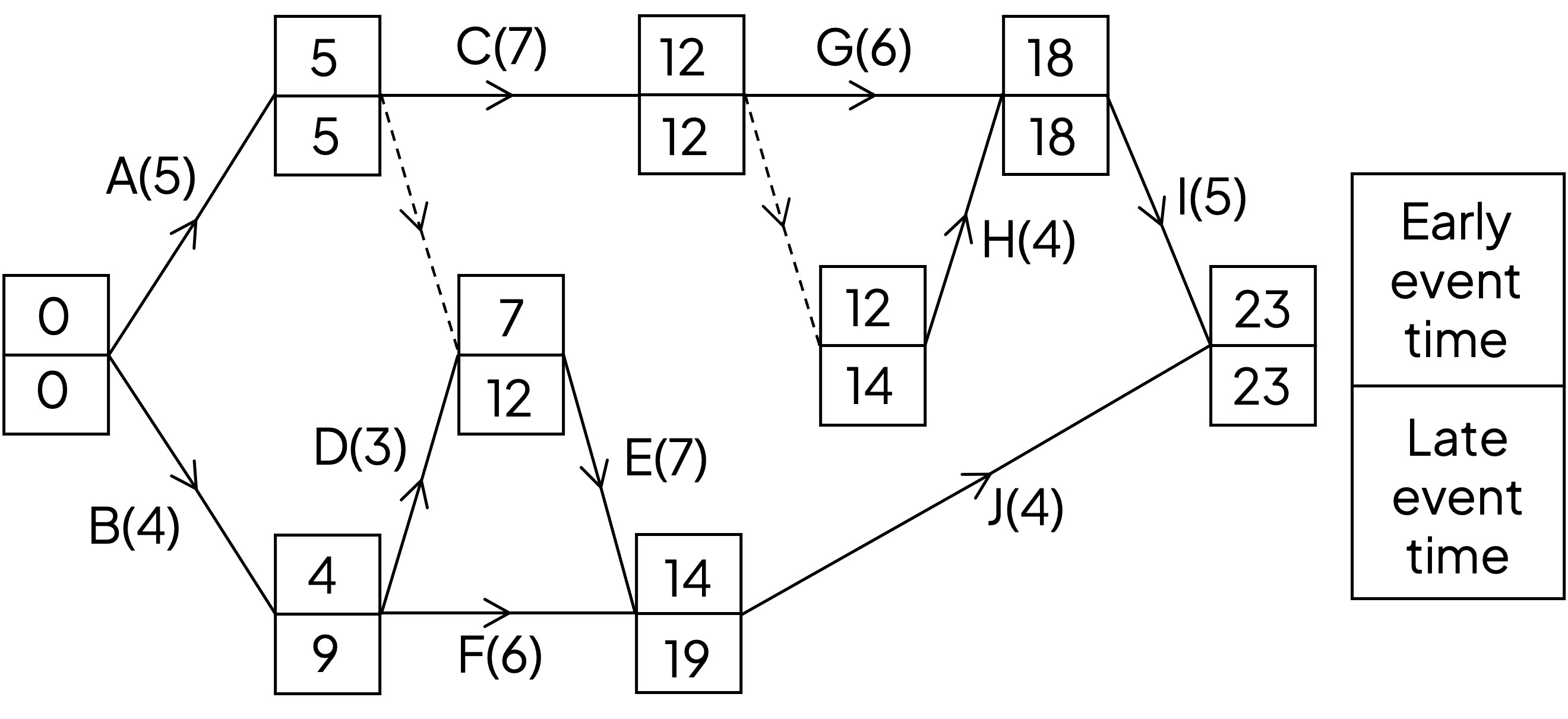
Find the total float for activities B, D, E, F and J.
For activity B, the late event time at its end node is 9, the early event time at its start node is 0, its duration is 4
Total float of B = 9 - 0 - 4 = 5
Activity D has late event time 12 at its end node, early event time 4 at its start node and duration 3
Total float of D = 12 - 4 - 3 = 5
Similarly for activities E, F and J
Total float of E = 19 - 7 - 7 = 5
Total float of F = 19 - 4 - 6 = 9
Total float of J = 23 - 14 - 4 = 5
The total floats are B:5, D:5, E:5, F:9, J:5
Critical Path & Critical Activities
What are the critical activities?
Critical activities
have a total float of zero
must commence at their earliest event time in order for the minimum project duration to be achieved
A critical event is an event where the earliest start time is equal to the latest finish time
To find the critical activities look for the critical events
If an activity is critical then the start and finish events must be critical
However the converse is not true
It is possible for a non-critical activity to be between two critical events
Critical activities should be stated as a list
E.g. the critical activities are A, C, D and G
What is a critical path?
A critical path through an activity network runs from the source node to the sink node
The activities along the path have a total float of zero
Each activity in a critical path will be critical
The critical path would be given in terms of the activities/arcs along the path
E.g. a critical path encompassing activities A, C, E, F and G would be written A - C - E - F - G
It is possible that there is more than one critical path through an activity network
E.g. A-C-D-G and A-C-E-F-G could both be critical paths
In this case the critical activities would be A, C, D, E, F, G
How do I find the minimum project duration?
The minimum project duration is the quickest time in which all activities in a project can be completed
It is found by completing the early event times for each node in an activity network
The early event time for the sink node is the minimum project duration
Examiner Tips and Tricks
Be clear about the difference between critical path and critical activities
Practically, these are found at the same time when analysing an activity network
Make sure you write both as would be expected
The critical path is a sequence of activities (sometimes written with '-' in between each)
e.g. A - B - D - F - GCritical activities would be a list, with a comma between each activity
E.g. A, B, D, F, G
Some problems may state that all activities have the same duration (without specify how long)
The critical path and critical activities can then be found by looking for the path from source node to sink node that has the fewest edges
Alternatively, pick any number (>0) for the duration of every activity and proceed as usual
1 is the most obvious choice of duration
This method would take far longer
Worked Example
The activity network below shows the duration (in days) of the activities needed to complete a project and the early and late times for each event.

Find the critical path, the critical activities and state the minimum project duration.
Start by looking at the nodes where the early and late event times are equal
Possible critical activities are A, C, G, I
Determine whether these activities have a total float of zero
Total float of A = 5 - 0 - 5 = 0
Total float of C = 12 - 5 - 7 = 0
Total float of G = 18 - 12 - 6 = 0
Total float of I = 23 - 18 - 5 = 0
Critical path is A-C-G-I
The critical activities are those that have a float of zero and lie along the critical path
Critical activities are A, C, G and I
The minimum project duration is the early (and late) event time at the sink node
Minimum project duration is 23 days

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?