Dummy Activities (Edexcel International AS Maths): Revision Note
Exam code: XMA01
Dummies
What is a dummy activity?
A dummy activity is an activity that has a weight of zero
Dummies are not assigned names (letters)
Dummies are represented by dotted lines
Dummies are only used to show precedences in more complicated activity networks
When and where are dummies used in an activity network?
Two situations can lead to the need for a dummy activity
The first situation is to ensure each activity (arc) has a unique pair of start and end nodes
E.g. In the activity network below, activity D has immediate predecessors B and C
B and C cannot both start at event (node) 1 and end at event (node) 2 (this would not be a unique pair)
a dummy activity is used so that B has start/end pair (1, 3) and C has start/end pair (1, 2)

Note that the dummy could also go from event 2 to event 3 with activity D commencing from event 3
The second situation that requires a dummy is when there is a split of immediate predecessors
E.g. In the activity network below, activity D has immediate predecessors B and C
Activity E only has B as an immediate predecessor
A dummy activity is used to show that D depends on both B and C

Examiner Tips and Tricks
Exam questions will not always require you to draw the whole activity network
A diagram of part of the network may be given
Exam questions are often specific about the number of dummies you should use
If you think you need more, go back to see if you can make improvements
It is generally expected that an activity network is as concise/efficient as possible with the minimum use of dummies
Worked Example
The activities involved in a project are listed in the precedence table below.
Activity | Immediately preceding activities | Duration (days) |
A | - | 5 |
B | - | 4 |
C | A | 7 |
D | B | 3 |
E | A, D | 7 |
F | B | 6 |
G | C | 6 |
H | C | 4 |
I | G, H | 5 |
J | E, F | 4 |
The project is also represented on the partially completed activity network below.
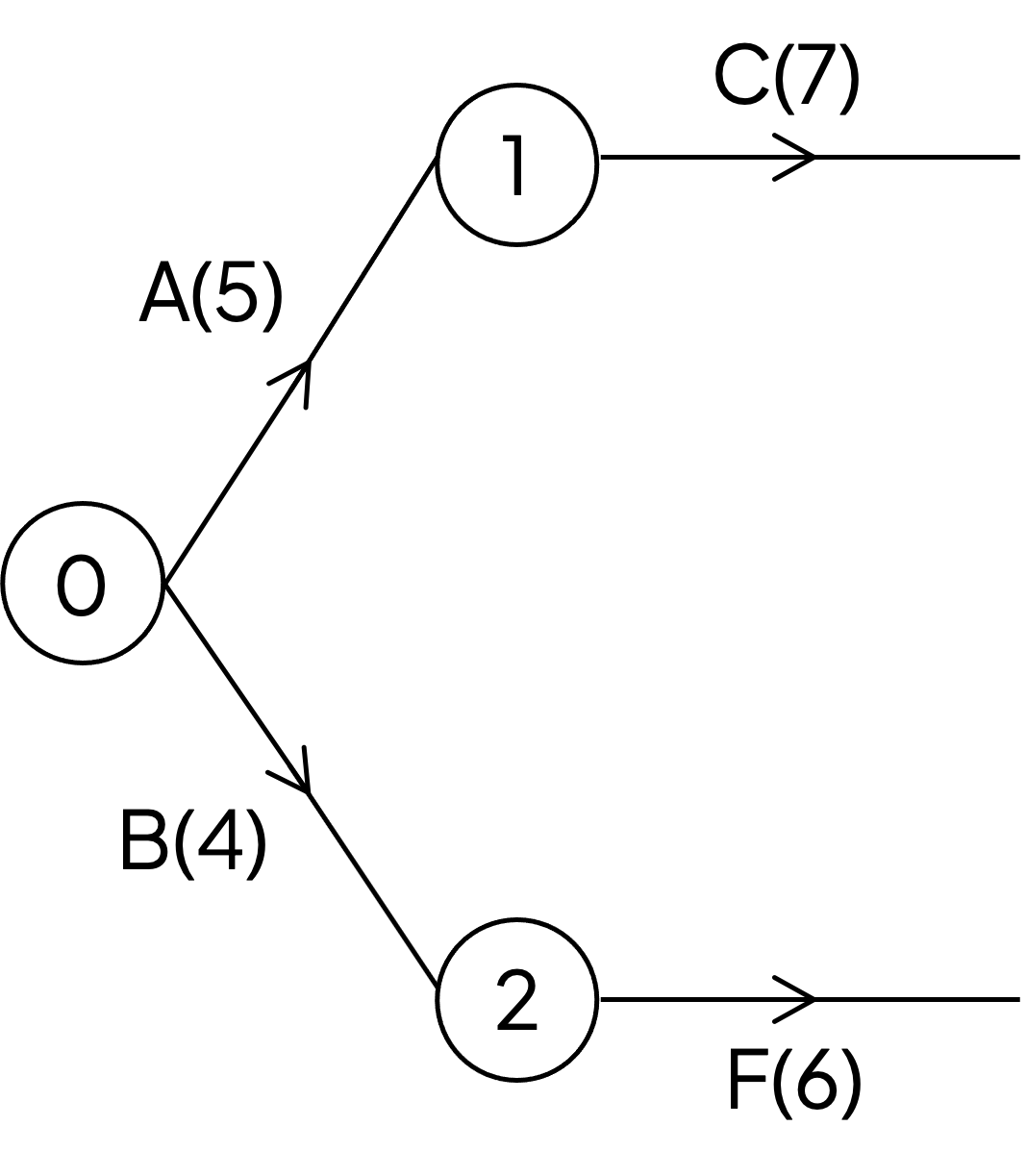
Using exactly two dummy activities, complete the activity network by adding activities D, E, G, H, I and J.
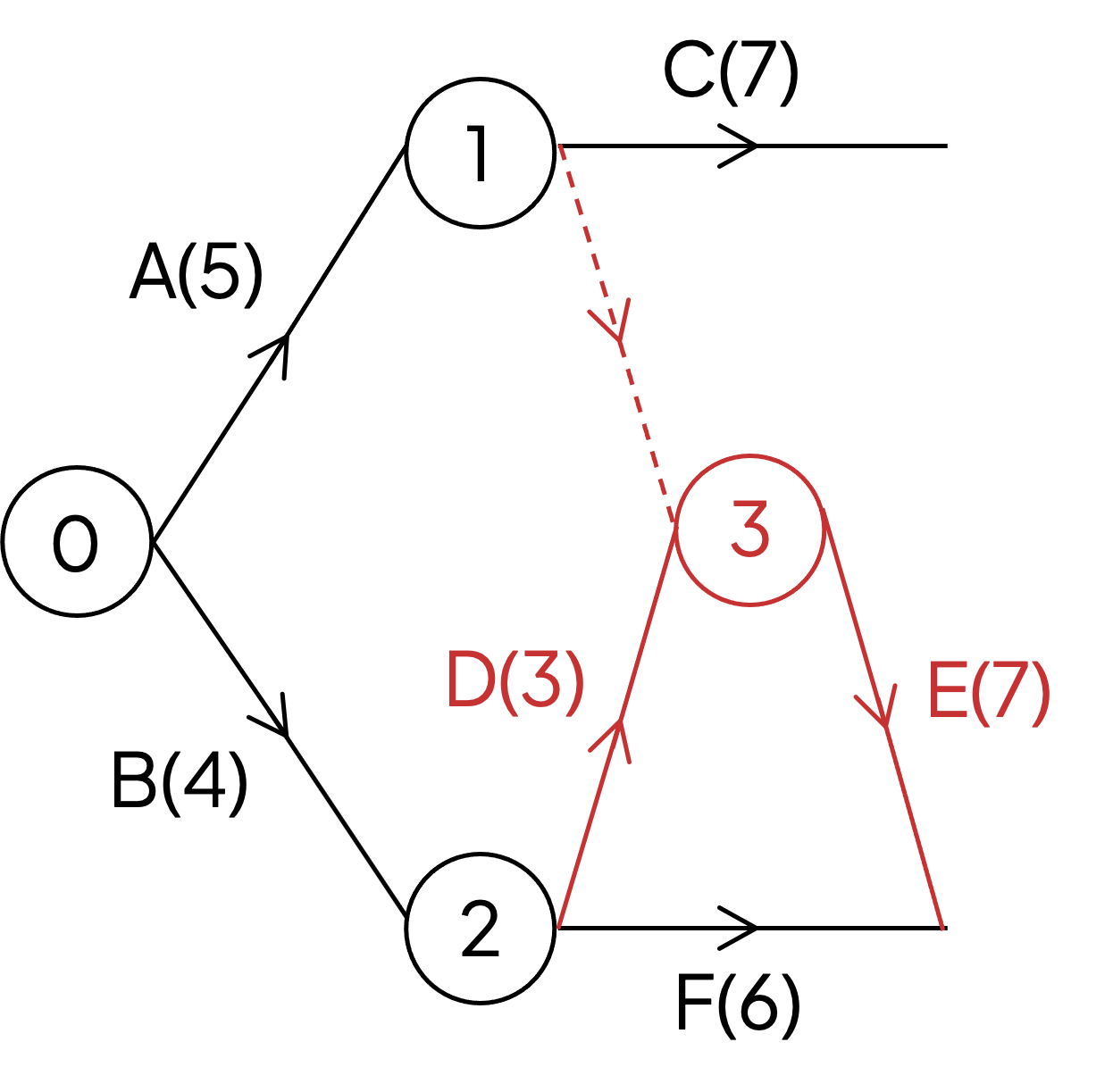
Activity D is dependent on activity B so draw an arc from event/node 2 for D
Looking ahead, activity E is dependent on both A and D, whereas activity C is dependent on just A
This is the second situation ('split predecessors') for the use of a dummy activity
Also from looking ahead activity J depends on both E and F - so the arcs for E and F will need to meet
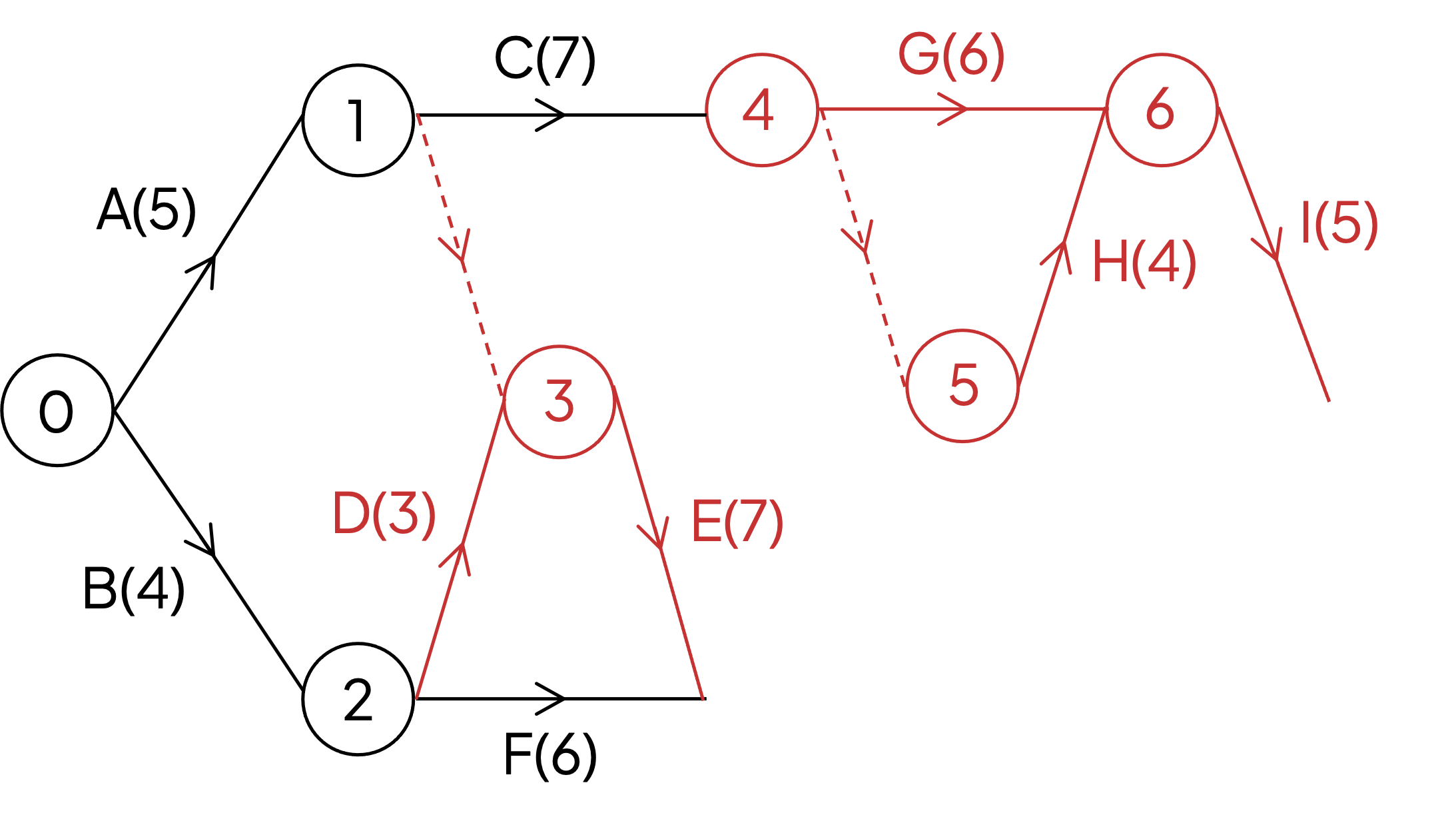
Activities G and H are both dependent on C, and activity I is dependent on both G and H
This could lead to G and H having the same start/end node pair
This is the first situation ('unique start/end node pair') for the use of a dummy activity
No activities depend on I so its arc can be drawn to the end of the project (sink node)
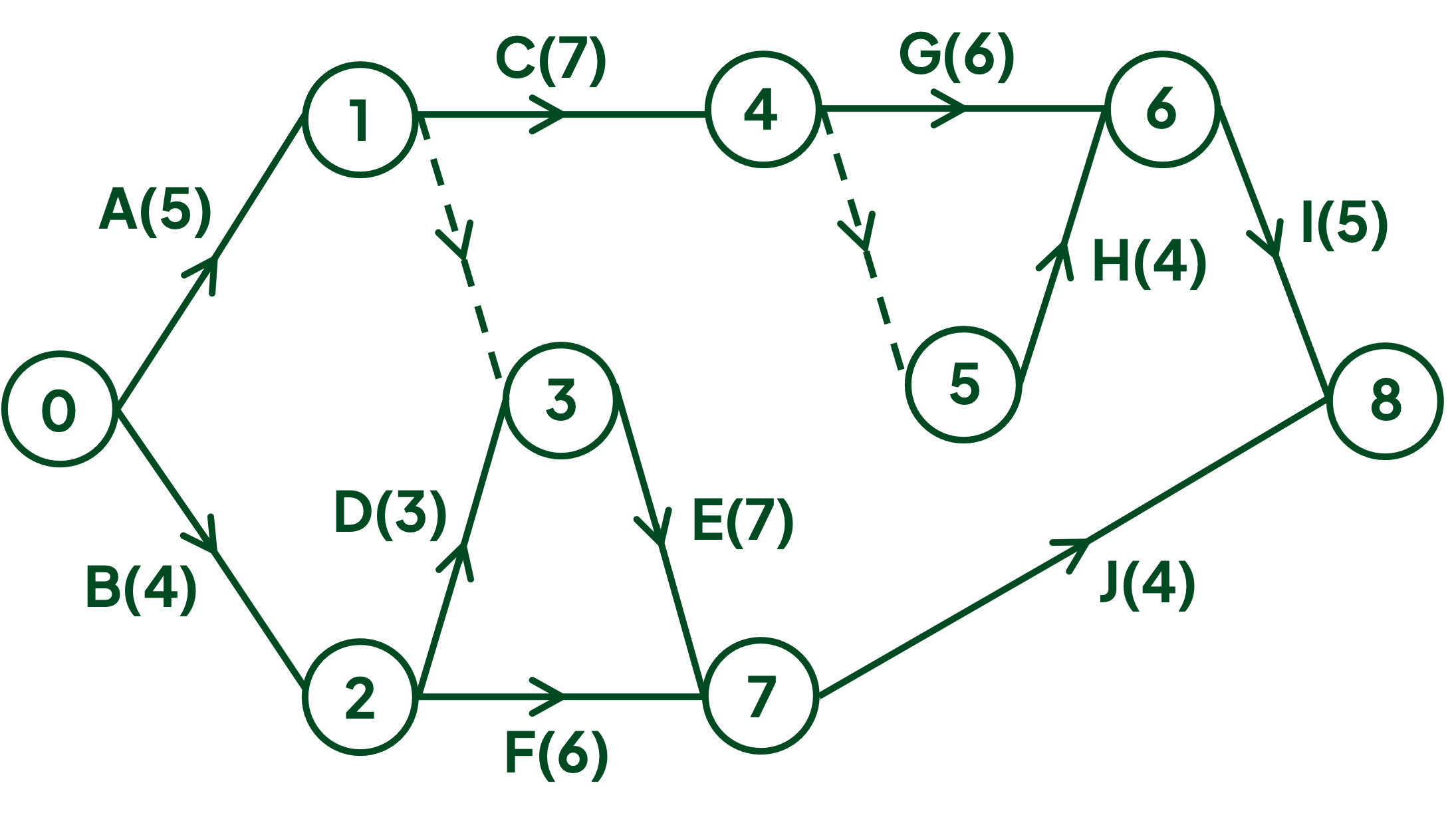
The activity network can now be completed with activity J and the sink node

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?