A LevelMathsEdexcelPureRevision NotesIntegrationDifferential EquationsModelling with Differential Equations

Modelling with Differential Equations (Edexcel A Level Maths): Revision Note

Exam code: 9MA0

Paul

Author

Paul

Last updated

Edexcel Maths: PureCambridge (CIE) Maths: Pure 3OCR Maths A: PureAQA Maths: Pure

Did this video help you?

Modelling with Differential Equations

What can be modelled with differential equations?

  • Derivative terms like  fraction numerator d y over denominator d x end fraction are “rates of change”

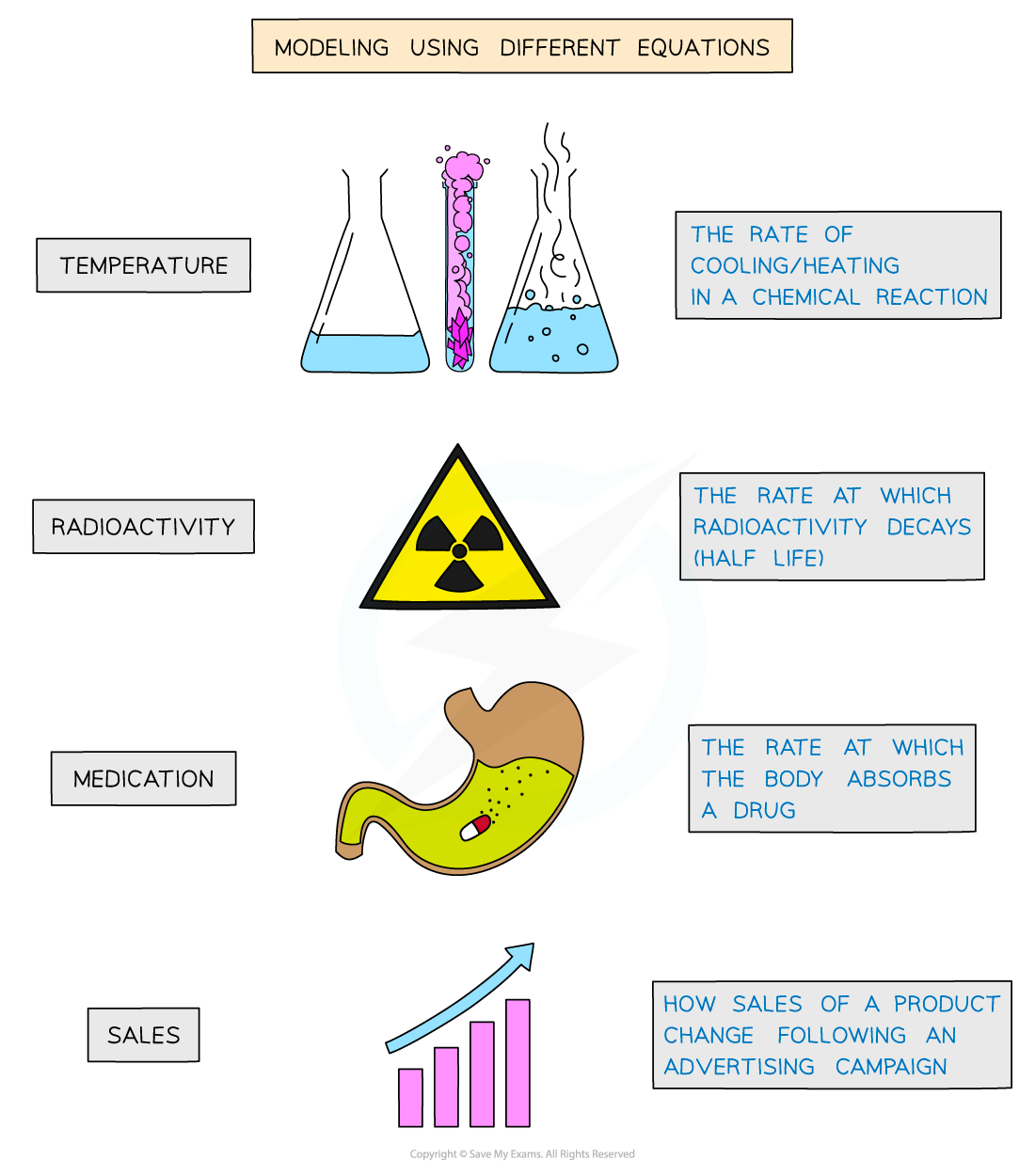
  •   There are many situations that involve “change”

  • Temperature

  • Radioactivity

  • Medication

  • Sales

Notes de_scenes, AS & A Level Maths revision notes

How do I set up a model with differential equations?

  • The first task is to set up a differential equation from a description in words:

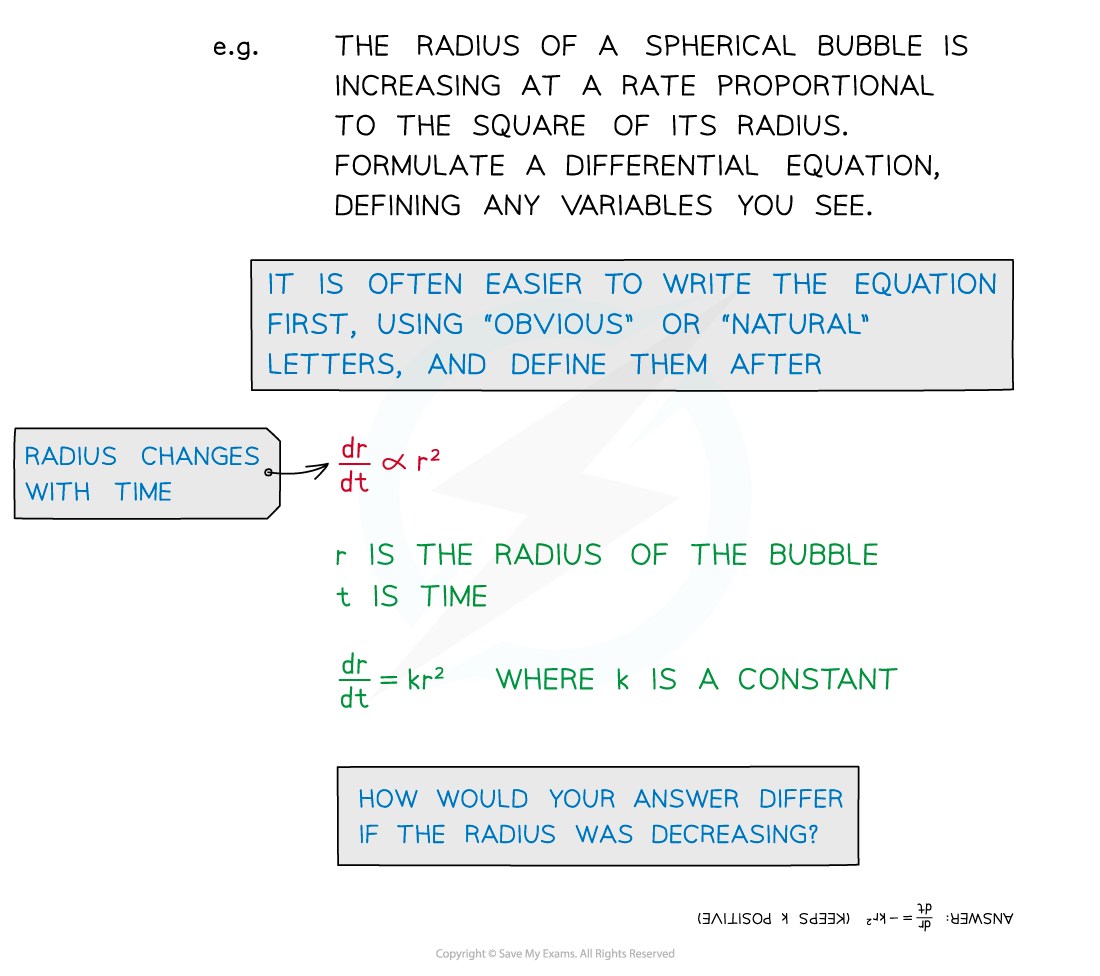
Notes de_setup, AS & A Level Maths revision notes

  • Important phrases here are …

    • … “rate of change” ... reference to a derivative term like fraction numerator d y over denominator d x end fraction

    • … directly/inversely proportional to ... y space equals space k x, y space equals k over x

    • … formulate ... means to write as an equation

      • you may need to choose and define letters for variables

      • V for volume, h for height (of a cylinder, say)

    8-3-4-notes-de-setup2

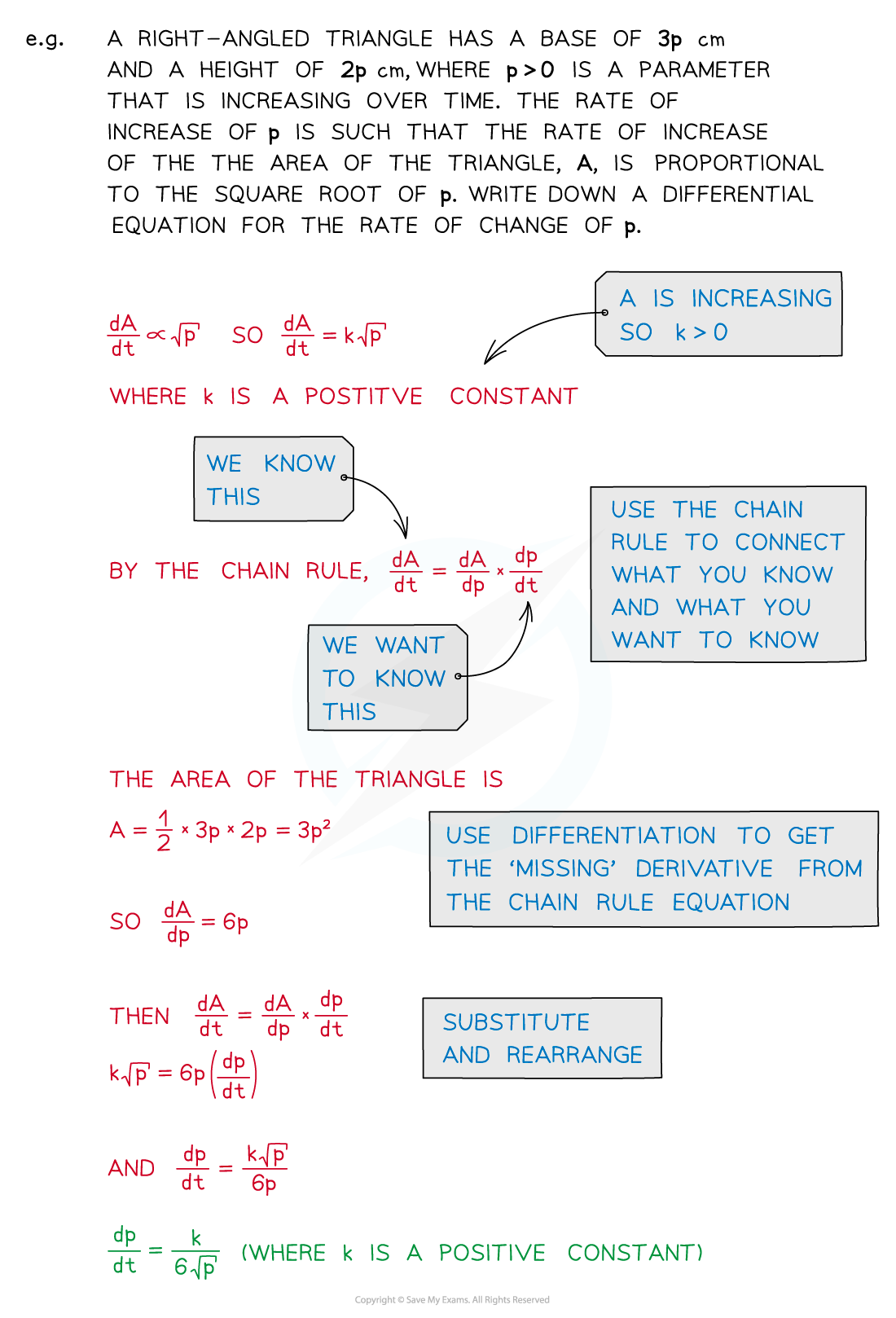
  • Some differential equations may involve Connected Rates of Change

 

Notes de_croc_setup, AS & A Level Maths revision notes

Examiner Tips and Tricks

  • Use a highlighter (or underline) to pick out important words/phrases

  • Read and re-read the question several times

  • Jot down bits and pieces as you go; do not expect to go straight from reading to writing down a differential equation.

Worked Example

Example soltn, AS & A Level Maths revision notes

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Separation of VariablesNext:Solving & Interpreting Differential Equations
Paul

Author: Paul

Expertise: Maths Content Creator

Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

Download notes on Modelling with Differential Equations