IBMathsDPApplications & Interpretation (AI)SLRevision Notes3. Geometry & TrigonometryGeometry of 3D ShapesVolume & Surface Area

Volume & Surface Area (DP IB Applications & Interpretation (AI)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Applications & Interpretation (AI): SLDP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

What is a prism?

  • A prism is a 3D shape that has two identical base shapes connected by parallel edges

    • A prism has the cross-section all the way through

  • Examples of prisms include:

    • Cubes

    • Cuboids

    • Triangular prisms

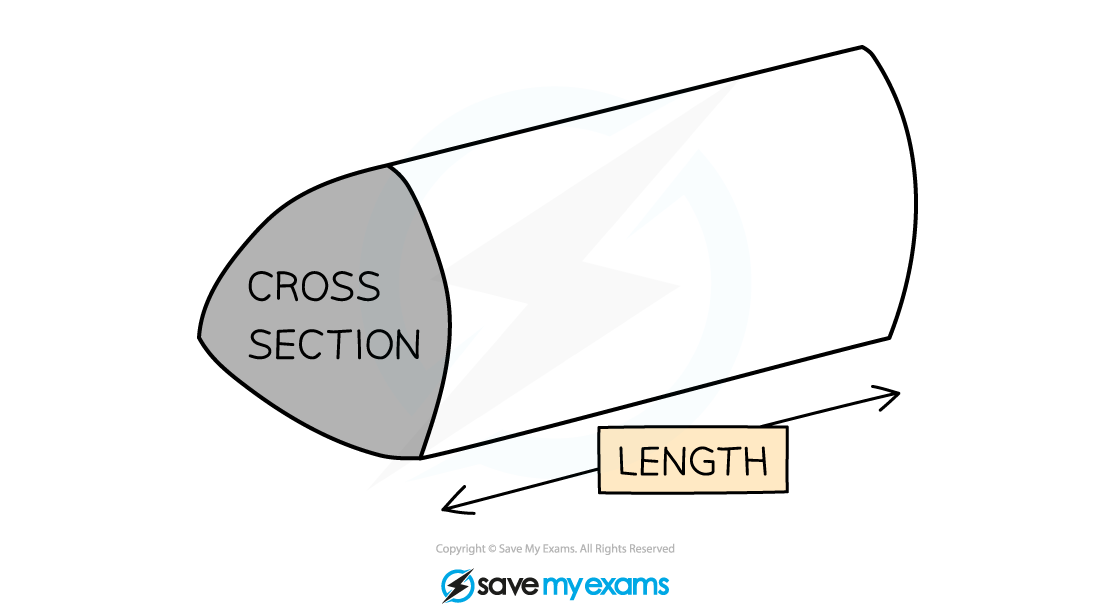
Diagram of a 3D shape with labelled cross-section and length, showing dimensions.
Example of a prism

  • A cylinder is not a prism

    • But it works in the same way as a prism

Diagram of a cylinder with radius "r" and height "h" labelled; dashed line indicates the base circle.
Example of a cylinder

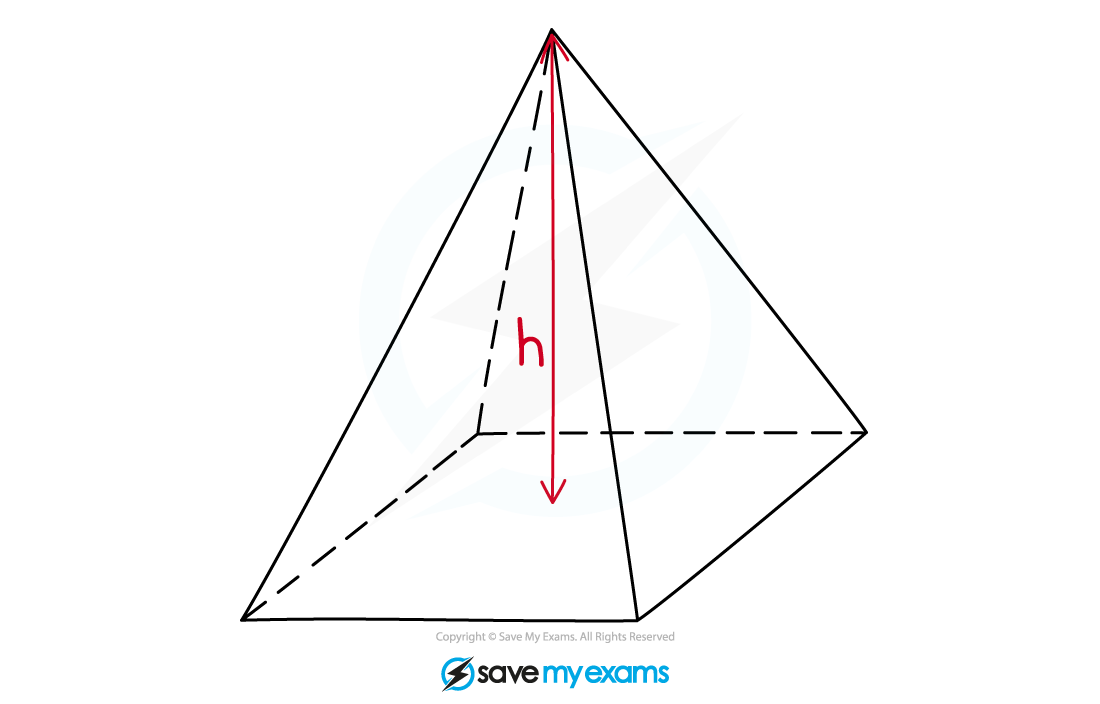
What is a pyramid?

  • A pyramid is a 3D shape that is made up of a base shape and an apex

    • Edges join the vertices of the base shape to the apex

  • Examples of pyramids include:

    • Square-based pyramids

    • Tetrahedron

    Illustration of a 3D pyramid with a dashed vertical line indicating height 'h' from the apex to the base. Dashed lines show hidden edges.
    Example of a pyramid

  • A cone is not a pyramid

    • But it works in the same way as a pyramid

Diagram of a cone with labelled height "h" and radius "r" at the base. A right angle is shown at the cone's base.
Example of a cone

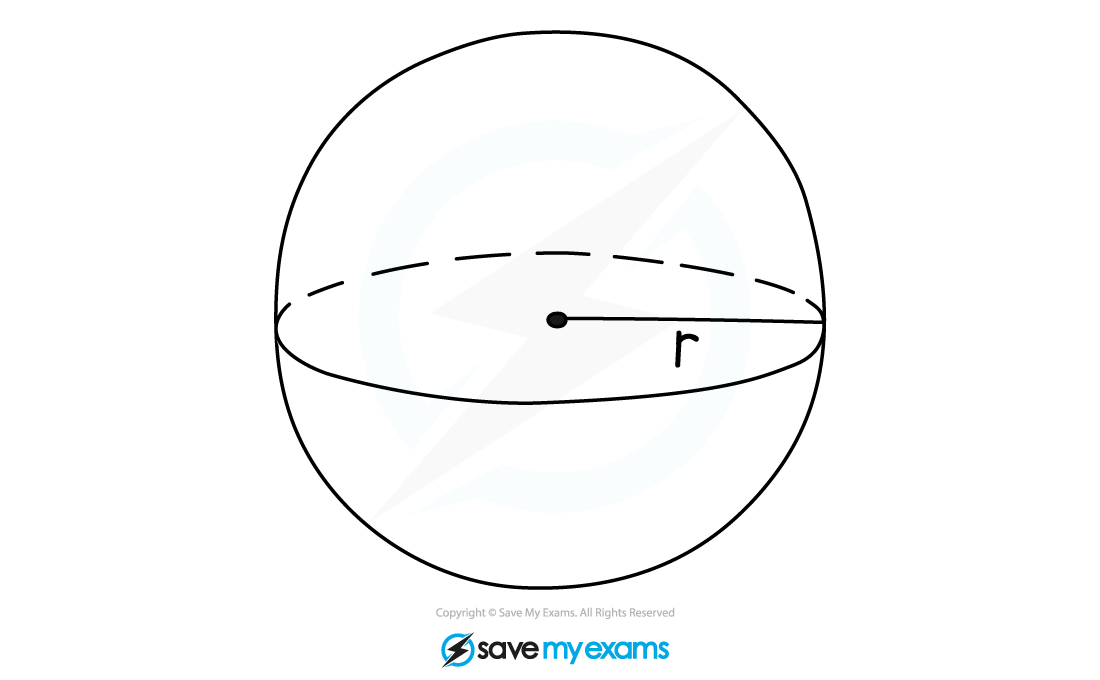
What is a sphere?

  • A sphere is a 3D shape created by all the points are a given distance from a centre

    • The distance is known as the radius

Diagram of a sphere with a horizontal dashed line, indicating a radius labelled 'r' from centre to surface.
Example of a sphere

Did this video help you?

Volume of 3D Shapes

How do I find the volume of prisms and cylinders?

  • The formula for the volume of a prism is V equals A h

    • V is the volume

    • A is the area of the cross-section

    • h is the height or length

  • The cross-section of a cuboid is a rectangle

    • The formula for the area of a rectangle is A equals l w

      • l is the length

      • w is the width

    • The formula for the volume of a cuboid is V equals l w h

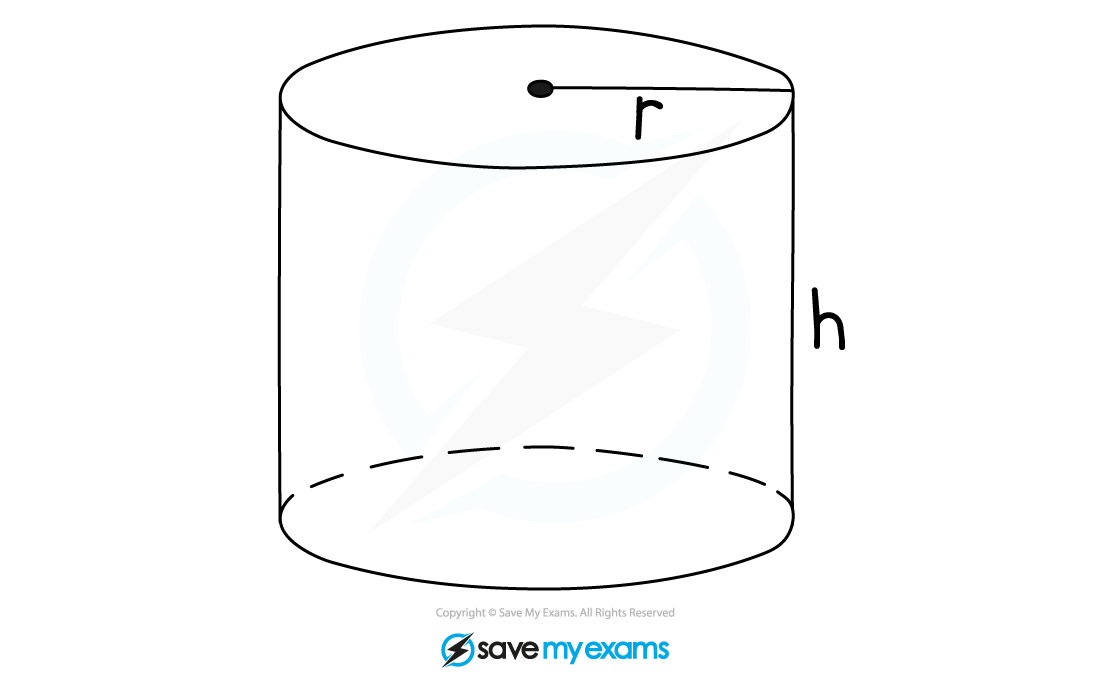
  • The cross-section of a cylinder is a circle

    • The formula for the area of a circle is A equals straight pi r squared

      • r is the radius

    • The formula for the volume of a cylinder is V equals straight pi r squared h

Examiner Tips and Tricks

All of these volume formulas are given in the formula booklet under the prior learning section.

How do I find the volume of pyramids and cones?

  • The formula for the volume of a pyramid is V equals 1 third A h

    • V is the volume

    • A is the area of the base

    • h is the height

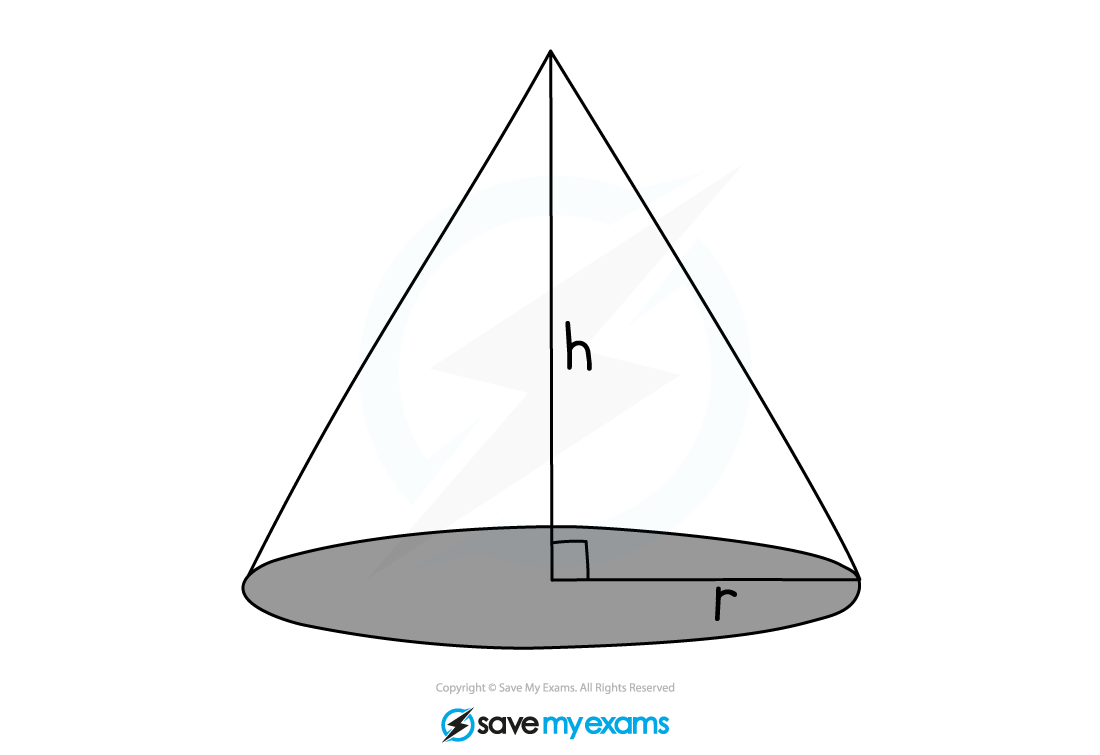
  • The base of a cone is a circle

    • The formula for the area of a circle is A equals straight pi r squared

      • r is the radius

    • The formula for the volume of a pyramid is V equals 1 third straight pi r squared h

Examiner Tips and Tricks

All of these volume formulas are given in the formula booklet under the geometry and trigonometry section.

How do I find the volume of a sphere?

  • The formula for the volume of a pyramid is V equals 4 over 3 straight pi r cubed

    • V is the volume

    • r is the radius

Examiner Tips and Tricks

This formula is given in the formula booklet under the geometry and trigonometry section.

Worked Example

A dessert can be modelled as a right-cone of radius 3 cm and height 12 cm and a scoop of ice-cream in the shape of a sphere of radius 3 cm.  Find the total volume of the ice-cream and cone.

diagram-for-we-3-2-2
3-2-2-ai-sl-volume-we-solution

Did this video help you?

Surface Area of 3D Shapes

How do I find the surface area of pyramids and prisms?

  • Find the surface area of a prism by adding together:

    • The areas of the two identical shapes at each end of the prism

    • The areas of the rectangles joining the two shapes

  • Find the surface area of a pyramid by adding together:

    • The area of the base shape

    • The areas of the triangles joining the base shape to the apex

How do I find the surface area of cylinders?

  • A cylinder is made up of two circles and a curved surface

  • The formula for the area of the curved surface of a cylinder is A equals 2 straight pi r h

    • r is the radius

    • h is the height or length

  • The formula for the surface area of a cylinder is A equals 2 straight pi r squared plus 2 straight pi r h

Examiner Tips and Tricks

The formula for the area of the curved surface is given in the formula booklet under the prior learning section. The formula for the surface area is not given.

How do I find the surface area of cones?

  • A cone is made up of a circle and a curved surface

  • The formula for the area of the curved surface of a cone is A equals straight pi r l

    • r is the radius

    • l is the slant height

  • The formula for the surface area of a cone is A equals straight pi r squared plus straight pi r l

Examiner Tips and Tricks

The formula for the area of the curved surface is given in the formula booklet under the geometry and trigonometry section. The formula for the surface area is not given.

How do I find the surface area of spheres?

  • The formula for the surface area of a sphere is A equals 4 straight pi r squared

    • r is the radius

Examiner Tips and Tricks

This formula is given in the formula booklet under the geometry and trigonometry section.

Worked Example

In the diagram below ABCD  is the square base of a right pyramid with vertex V .  The centre of the base is M. The sides of the square base are 3.6 cm and the vertical height is 8.2 cm.

sa-diagram-for-we-3-2-2

i) Use the Pythagorean Theorem to find the distance VN.

 

3-2-2-ai-sl-surface-area-we-solution-i

ii) Calculate the area of the triangle ABV.

 

3-2-2-ai-sl-surface-area-we-solution-ii

iii) Find the surface area of the right pyramid.

3-2-2-ai-sl-surface-area-we-solution-iii
👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It’s free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:3D Coordinate GeometryNext:Pythagoras & Right-Angled Trigonometry
Author
Reviewer
Amber

Author: Amber

Expertise: Maths Content Creator

Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Volume & Surface Area