Maths Skill: Using a Tangent to Find Initial Rate of Reaction (AQA AS Biology): Revision Note
Exam code: 7401
Using a tangent to find the initial rate of reaction
For linear graphs (i.e. graphs with a straight line), the gradient is the same throughout
This makes it easy to calculate the rate of change (rate of change = change ÷ time)
The initial rate of reaction is the rate of reaction at the start of the line (i.e. where time = 0)
However, many enzyme rate experiments produce non-linear graphs (i.e. graphs with a curved line), meaning they have an ever-changing gradient
They are shaped this way because the reaction rate is changing over time
In these cases, a tangent can be used to find the reaction rate at any one point on the graph:
Worked Example
The graph below shows the results of an enzyme-catalysed reaction. Using this graph, calculate the initial rate of reaction.

Step 1: Estimate the extrapolated curve of the graph
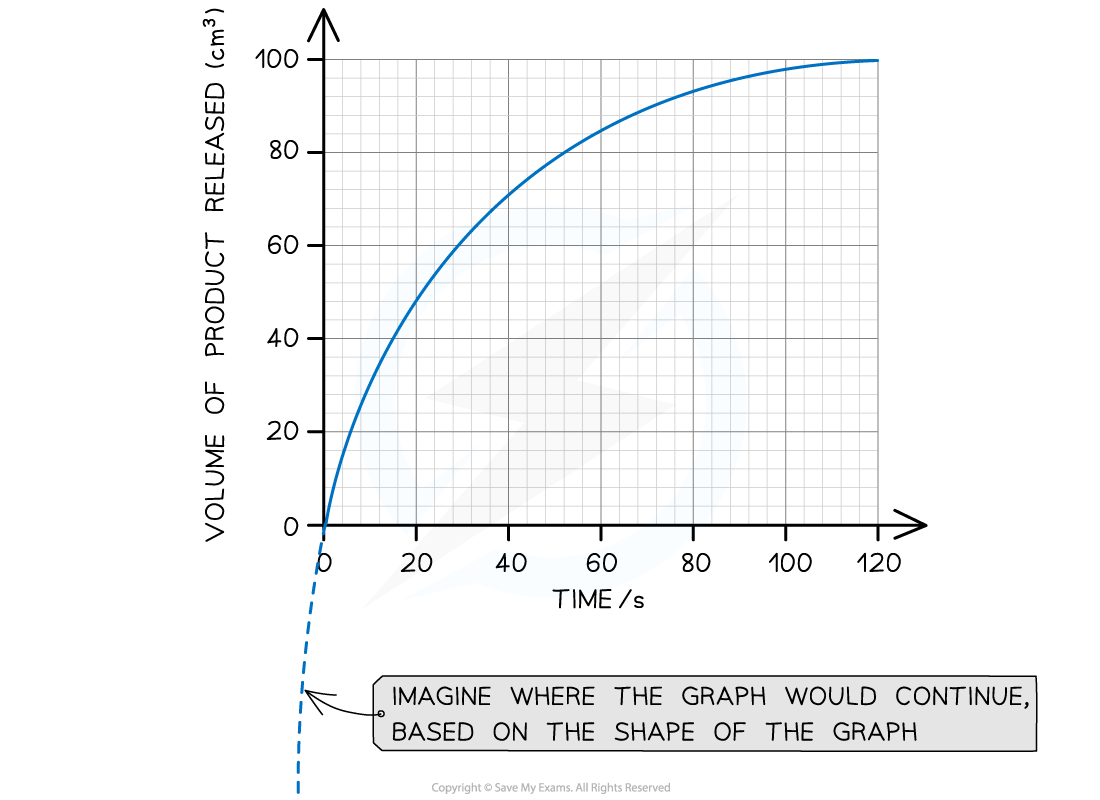
Step 2: Find the tangent to the curve at 0 seconds (the start of the reaction)
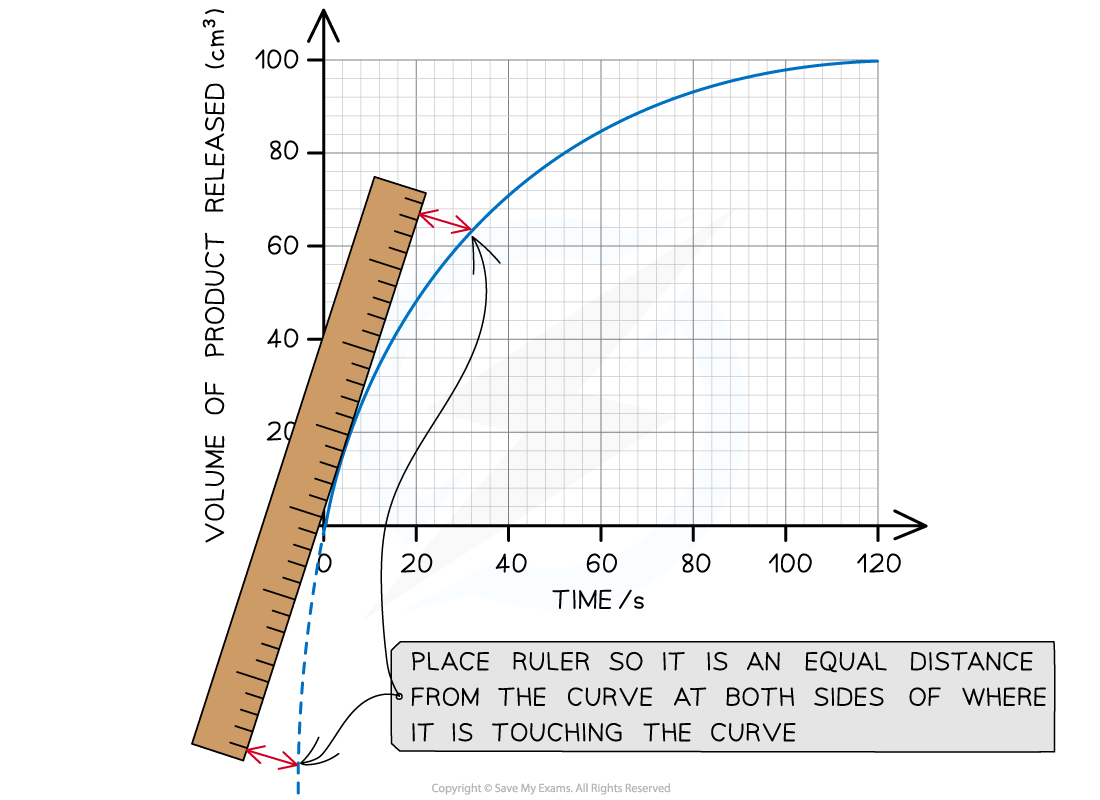
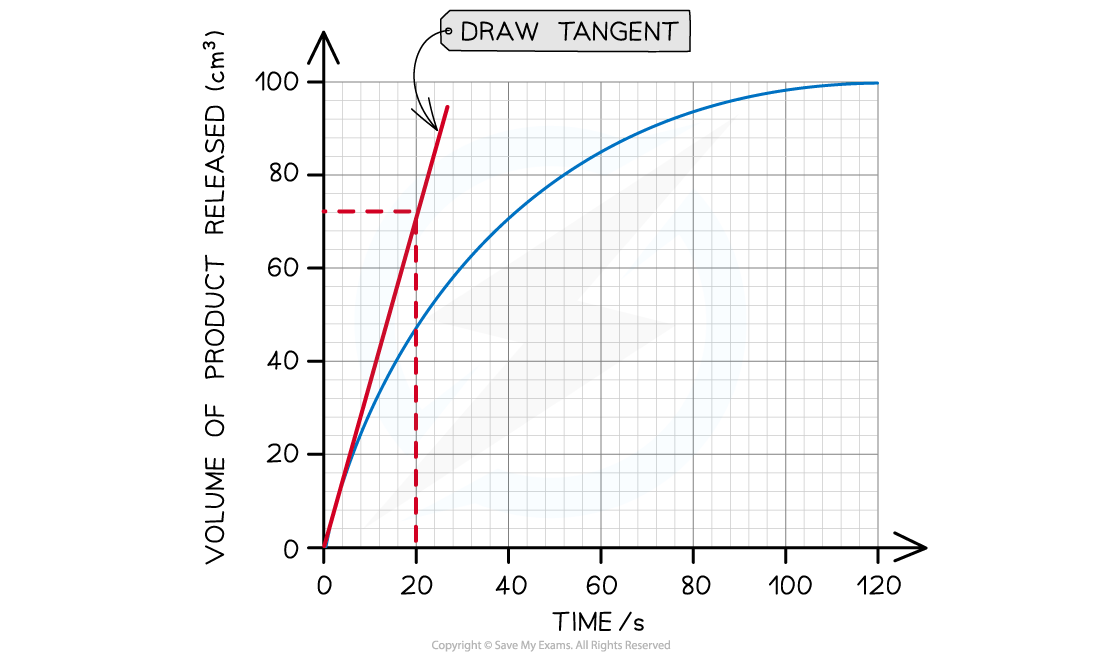
The tangent drawn in the graph above shows that 72 cm3 of product was produced in the first 20 seconds.
Step 3: Calculate the gradient of the tangent (this will give you the initial rate of reaction):
Gradient = change in y-axis ÷ change in x-axis
Initial rate of reaction = 72 cm3 ÷ 20 s
Initial rate of reaction = 3.6 cm3 s-1
Examiner Tips and Tricks
When drawing a tangent, use a ruler and pencil to draw a perfectly straight line that just touches the curve at the chosen point. Make sure the curve remains visible (not hidden under the ruler).
To calculate the gradient, remember this handy phrase:
"Rise over run" – divide the vertical change by the horizontal change.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

