Linear Inequalities (Edexcel AS Maths): Revision Note
Exam code: 8MA0
Did this video help you?
Linear inequalities
What are linear inequalities?
Linear inequalities are similar to equations but answers take a range of values
Linear means there will be no terms other than degree 1
no squared terms or higher powers, no fractional or negative powers
Inequalities use the symbols following symbols
Greater than e.g.
Less than e.g.
Greater than or equal to
Less than or equal to
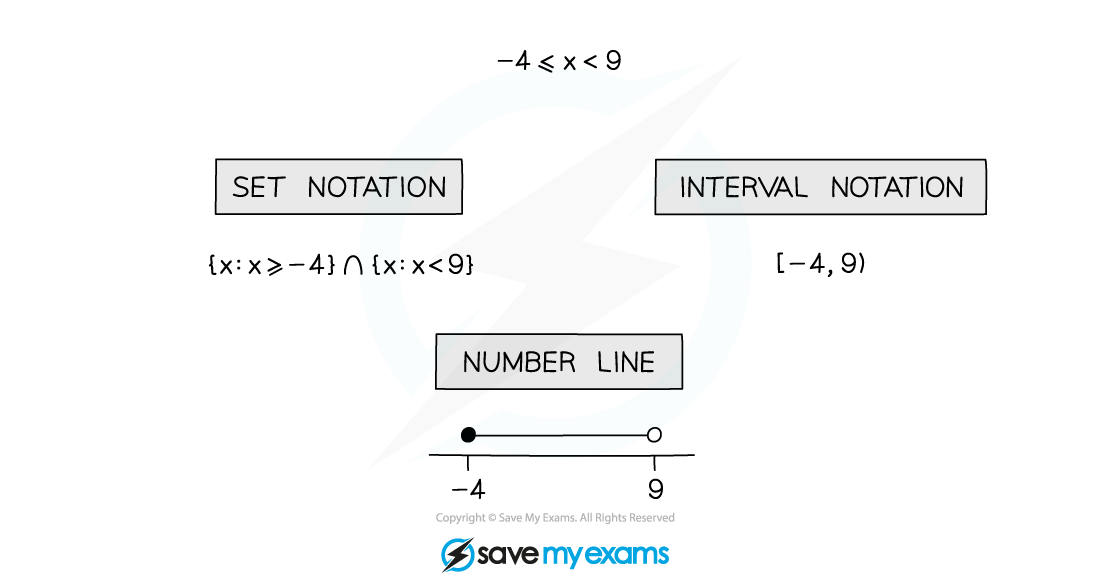
Inequalities can be represented in many ways using number lines, set notation and interval notation
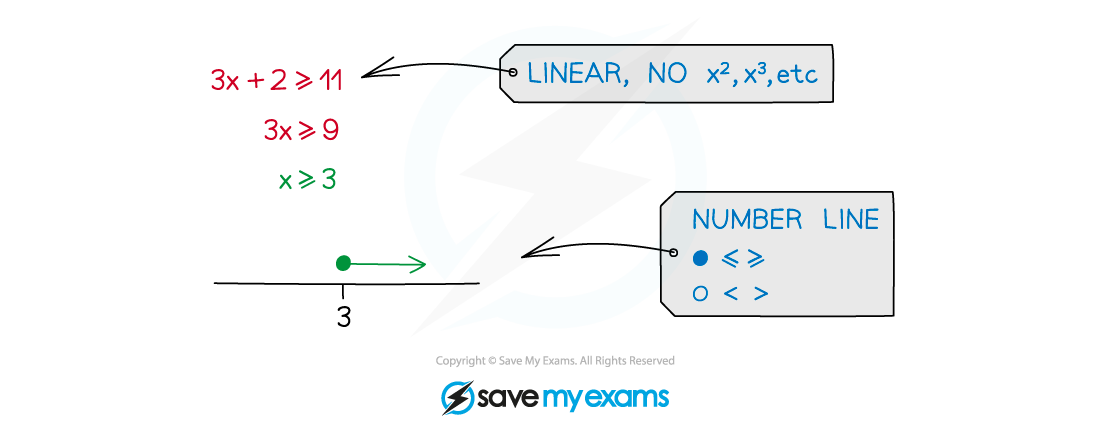
How do I use number lines?
Number line diagrams are made up from circles and lines set above a number line
A filled-in circle or empty circle above a number denotes whether the number is included or not
filled in for the greater/less than or equal to symbols
empty for the greater/less than symbols
Arrows show the range of values that are allowed
How do I use set notation for inequalities?
Set notation is a formal way of writing a range of values
Use of curly brackets { }
Intersection ∩ and union ∪ may be used
Not to be confused with interval notation

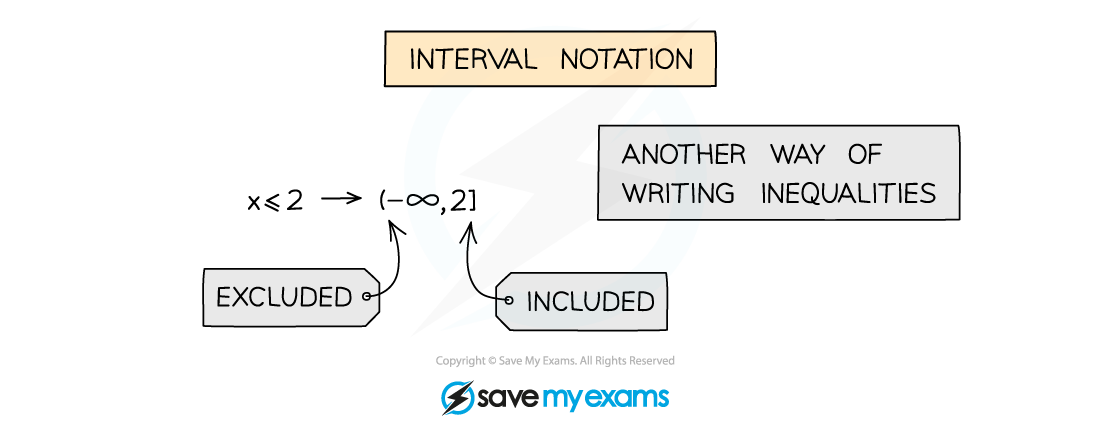
How do I use interval notation for inequalities?
Interval notation uses different brackets to indicate whether a number is included or not
Use of square [] and round () brackets
[ or ] mean included
( or ) mean excluded
(4,8] means 4 < x < 8
Note ∞ always uses ( or )
Not to be confused with set notation
Skills for solving linear inequalities
representing and interpreting inequalities displayed on a number line
writing and interpreting set notation
eg {x : x > 1} ∩ {x : x ≤ 7} is the same as 1 < x ≤ 7
writing and interpreting interval notation
eg [-4, 6) is the same as -4 ≤ x < 6
How do I solve linear inequalities?
Treat the inequality as an equation and solve
avoid multiplying or dividing by a negative
if unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc
try to rearrange to make the x term positive

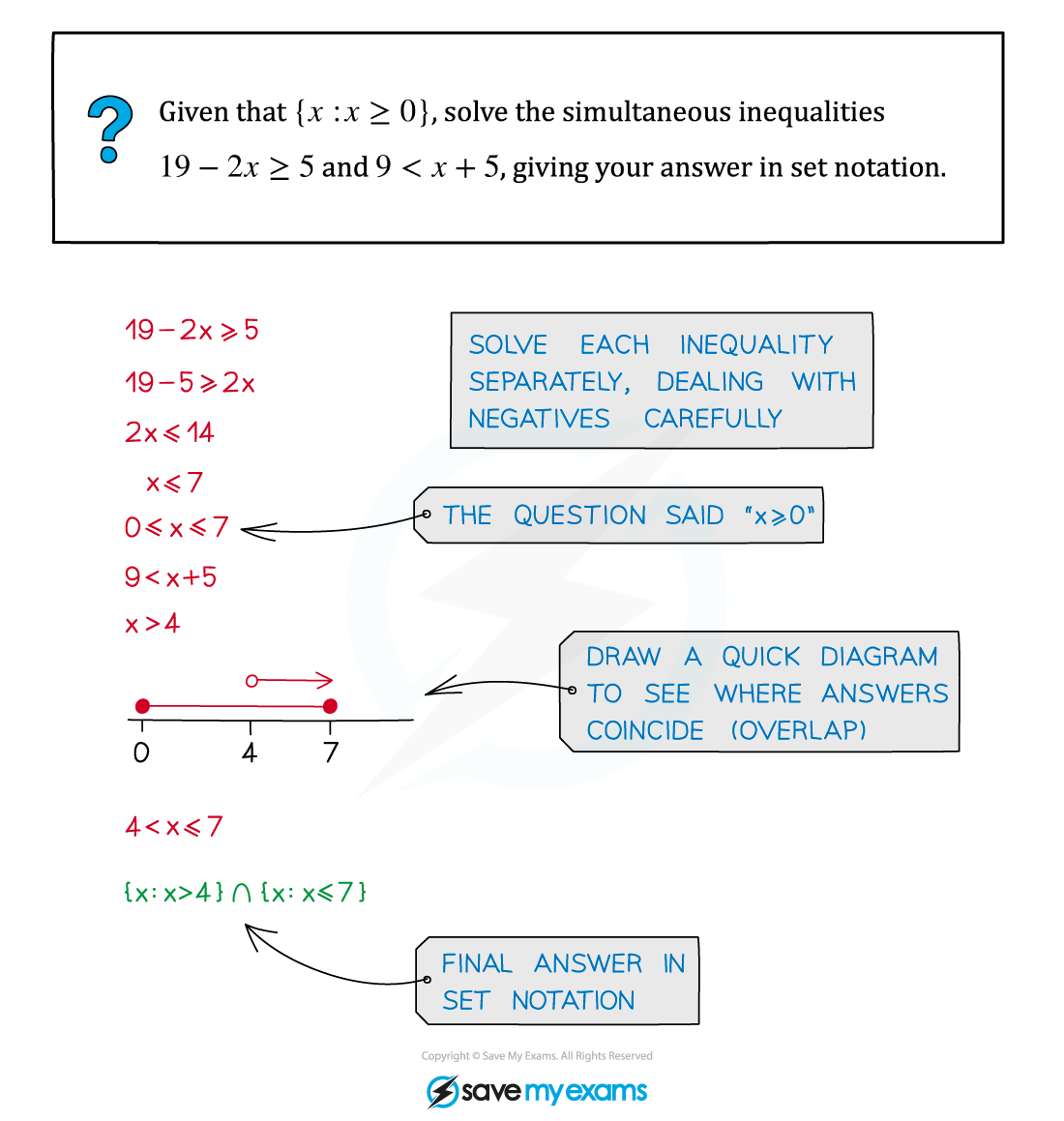
Worked Example

Unlock more, it's free!
Did this page help you?