Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)SLRevision Notes2. FunctionsFurther Functions & GraphsCubic Functions & Graphs

Cubic Functions & Graphs (DP IB Applications & Interpretation (AI)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Updated on

DP Applications & Interpretation (AI): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SL

Cubic functions & graphs

What are the key features of cubic graphs?

  • A cubic graph is of the form space y equals a x cubed plus b x squared plus c x plus d where space a not equal to 0.

  • The value of a affects the shape of the curve

    • If a is positive the graph goes from bottom left to top right

    • If a is negative the graph goes from top left to bottom right

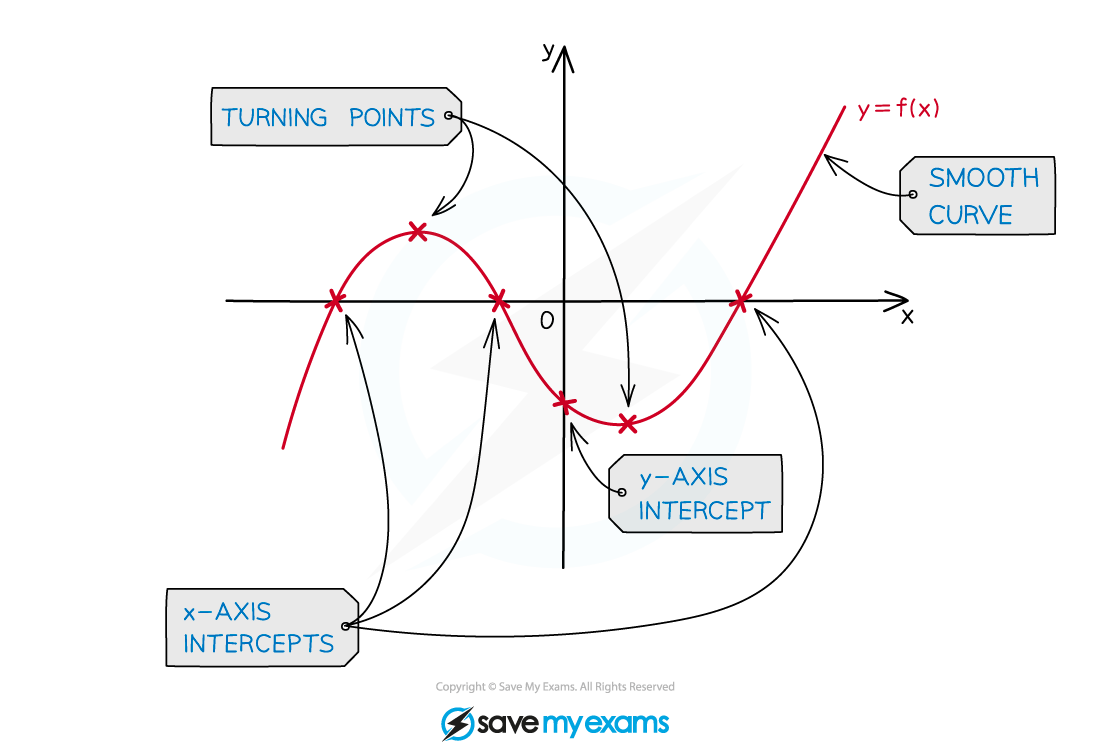
  • The y-intercept is at the point left parenthesis 0 comma space d right parenthesis

  • The zeros or roots are the solutions to space a x cubed plus b x squared plus c x plus d equals 0

    • These can be found using your GDC

    • These are also called the x-intercepts

    • There can be 1, 2 or 3 x-intercepts

      • There is always at least 1

  • There are either 0 or 2 local minimums/maximums

    • If there are 0 then the curve is monotonic

    • If there are 2 then one is a local minimum and one is a local maximum

Graph of the function y=f(x) with smooth curve, showing x-axis and y-axis intercepts, and turning points. Labels indicate key features.
Example of a cubic graph and its key features

Examiner Tips and Tricks

You can use your GDC to find the roots, the local maximum and local minimum of a cubic function.

When drawing/sketching the graph of a cubic function be sure to label all the key features

  • x and y axes intercepts

  • the local maximum point

  • the local minimum point

Worked Example

Sketch the graph space y equals 2 x cubed minus 6 x squared plus x minus 3.

2-2-3-ib-ai-sl-quad--cub-graphs-c-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Quadratic Functions & GraphsNext:Exponential Functions & Graphs
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Reviewer: Lucy Kirkham

    Expertise: Head of Content Creation

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.