Solving & Interpreting Differential Equations (Edexcel International A Level (IAL) Maths): Revision Note
Exam code: YMA01
Did this video help you?
Solving & interpreting differential equations
How do I solve a differential equation from a given model?
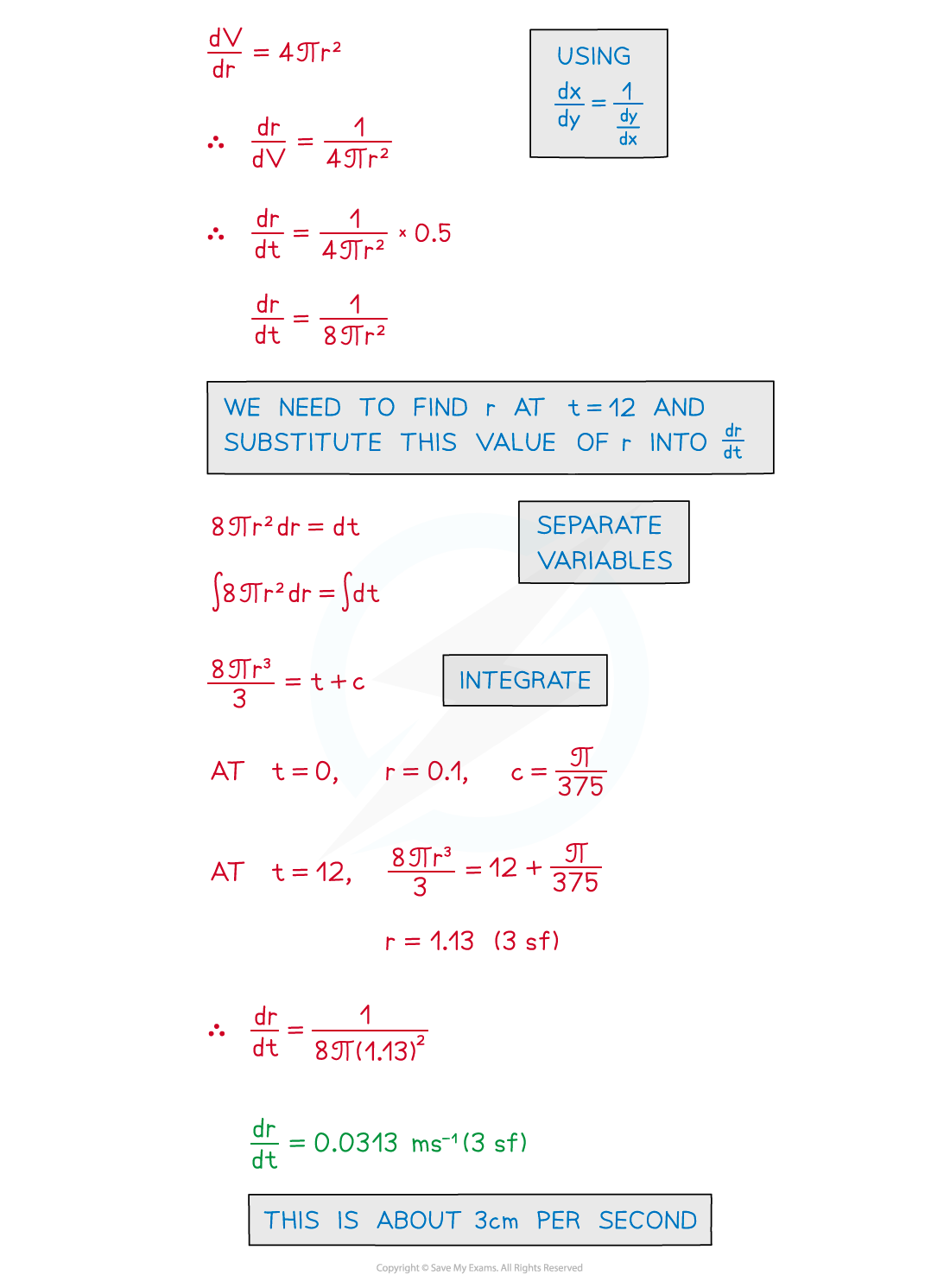
Solving differential equations from a given model using the same techniques as before, for example separation of variables
The precise integration method will depend on the type of question (see Decision Making)
Particular solutions are usually required to Differential Equations
An initial/boundary condition is needed

Solutions can be rewritten in a format relevant to the model
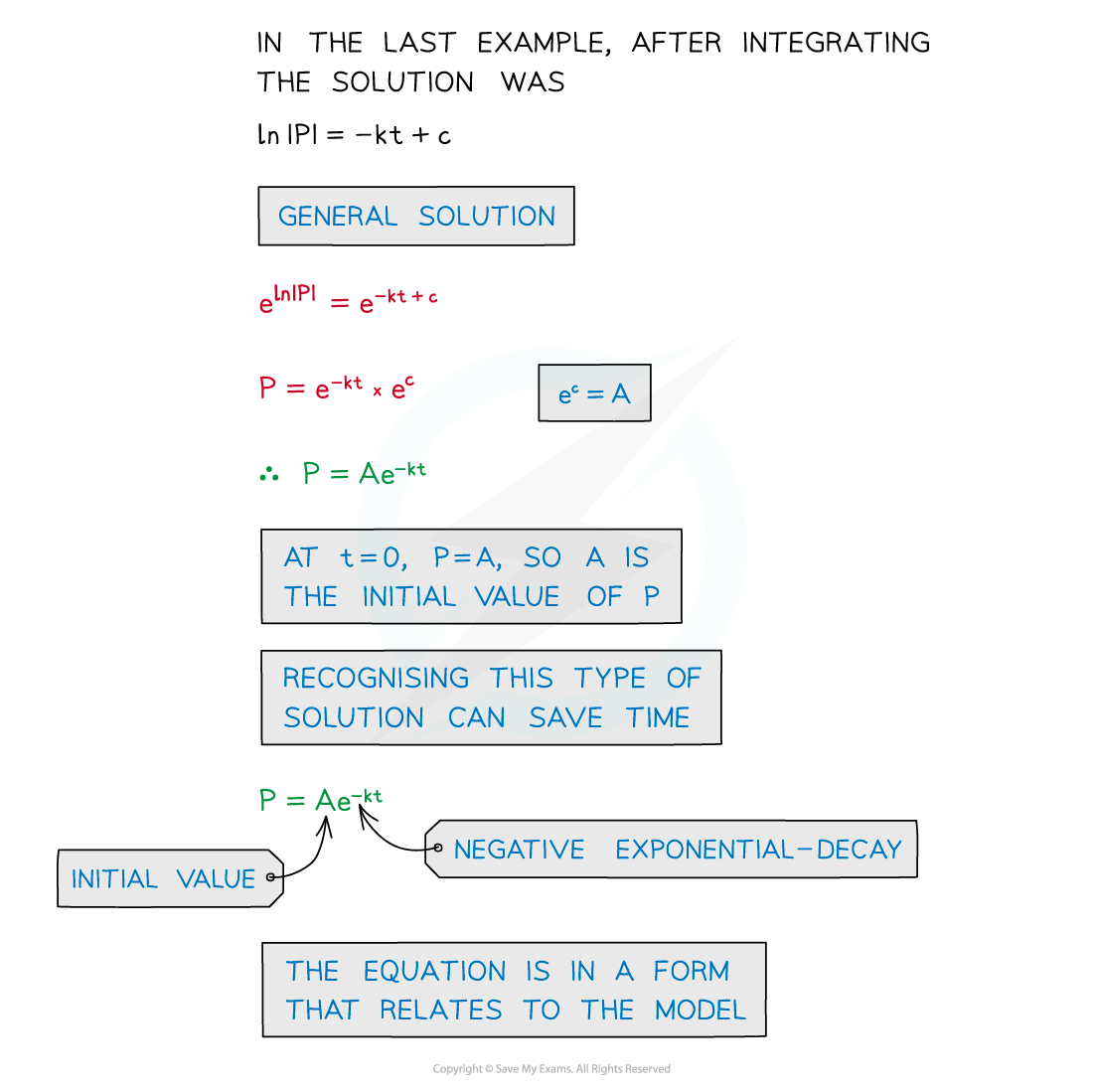
The solution can be used to make predictions at other times
Temperature after four minutes
Volume of sales after another three months
How can I use the solution of a differential equation to answer modelling questions?
Questions may ask you to interpret your solutions in the context of the problem

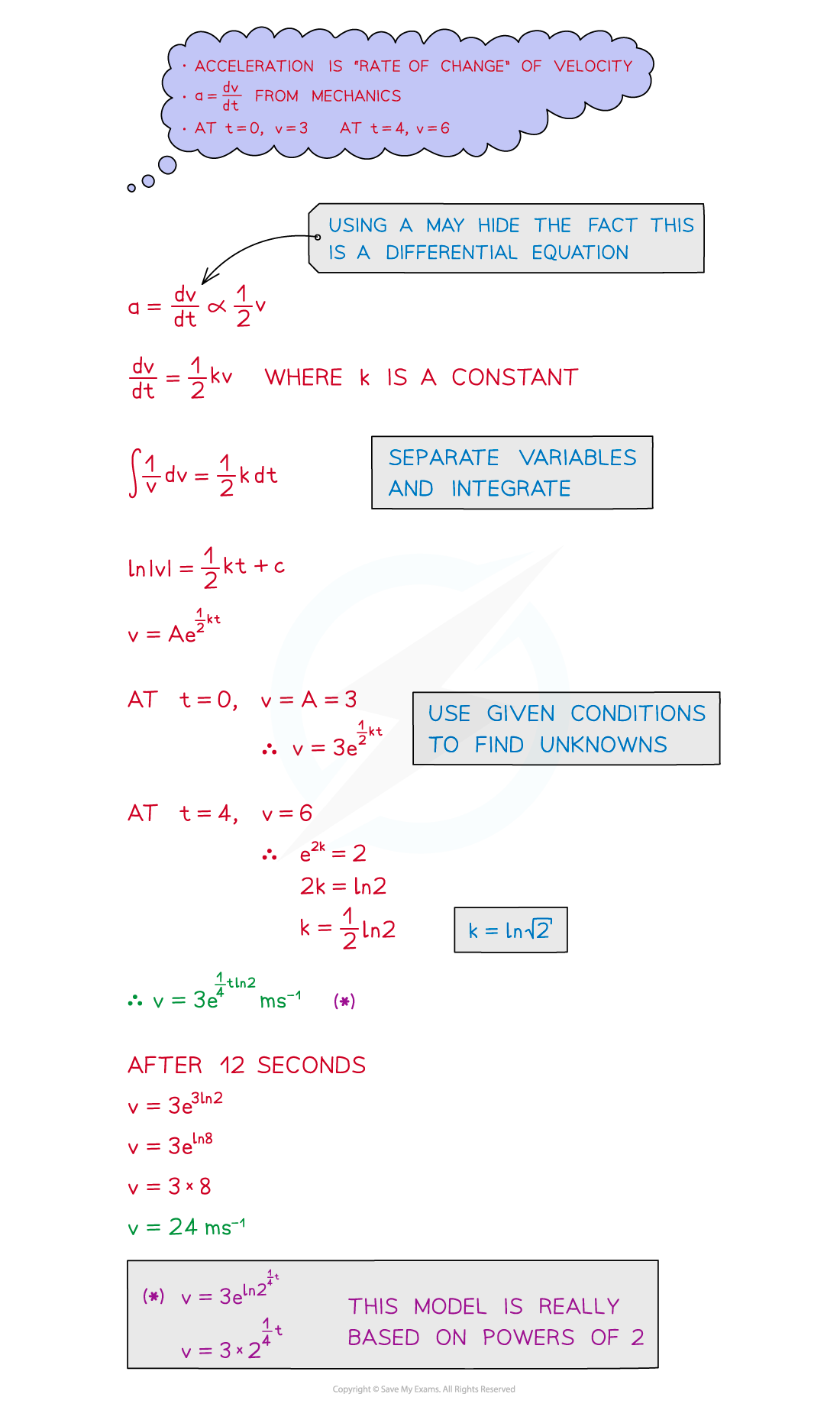
There could be links to other areas of A level maths – such as mechanics

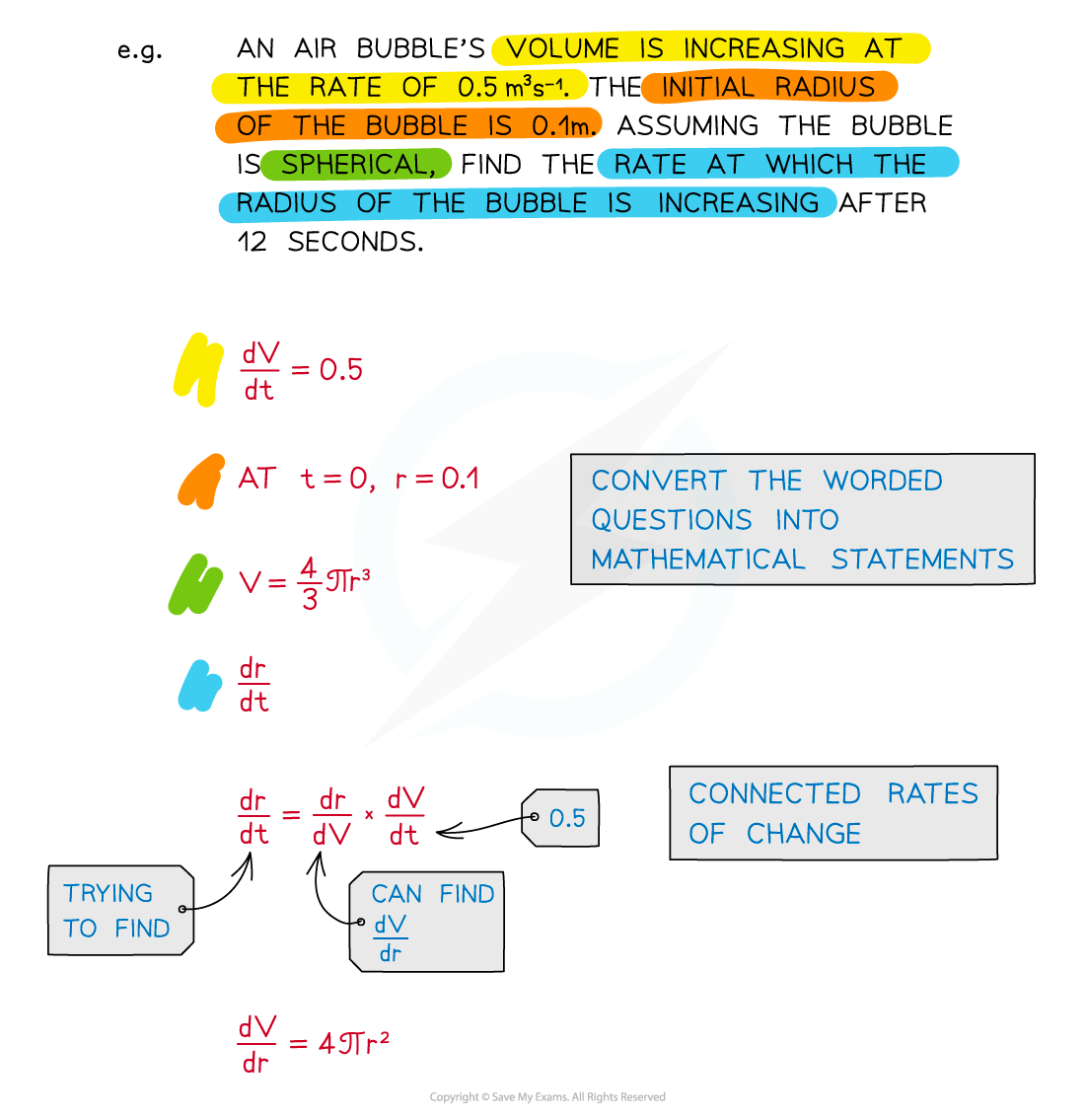
Sometimes multiple rates of change may be involved in a model or problem
See Connected Rates of Change
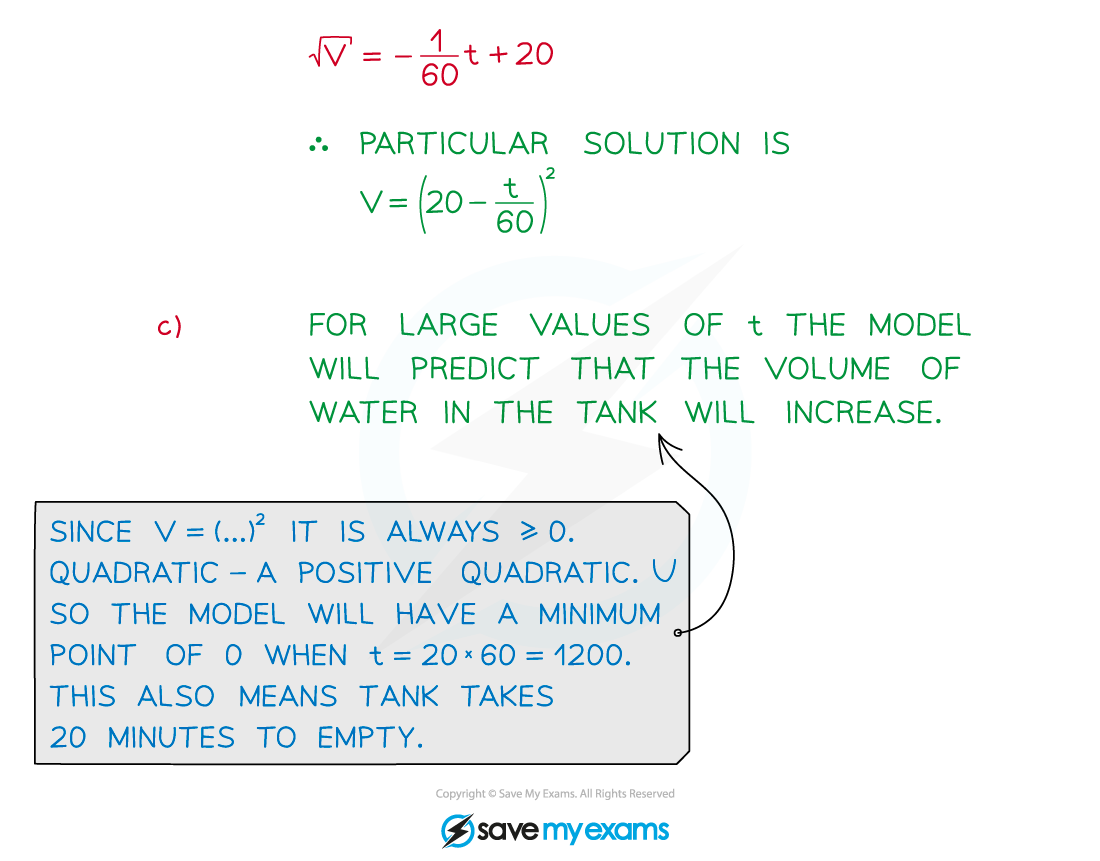
How can I interpret a model using the solution to the differential equation?
Models may not always be realistic in the long term
A population will not grow indefinitely – it will reach a natural limit
You will be expected to interpret and comment on the model

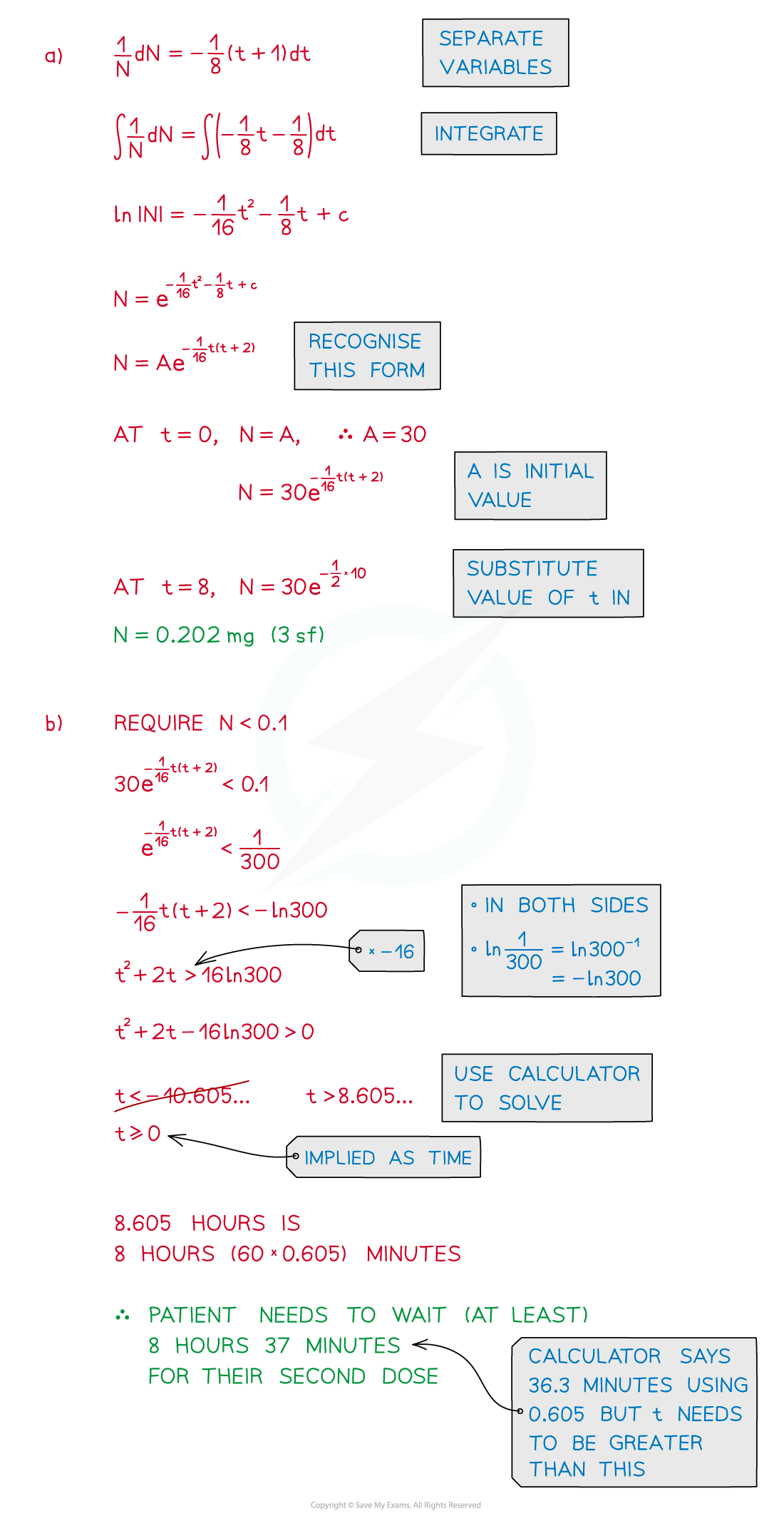
Worked Example


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?