A LevelMathsCambridge (CIE)MechanicsRevision NotesKinematics (Straight Line Motion)Kinematics GraphsDisplacement-Time Graphs

Displacement-Time Graphs (Cambridge (CIE) A Level Maths): Revision Note

Exam code: 9709

Dan Finlay

Last updated

Cambridge (CIE) Maths: MechanicsOCR Maths A: MechanicsAQA Maths: MechanicsEdexcel Maths: Mechanics

Did this video help you?

Displacement-Time Graphs

What is a displacement-time graph?

  • Displacement-time graphs show the displacement of an object from a fixed origin as it moves in a straight line

  • They show displacement (on the vertical axis) against time (on the horizontal axis)

  • Displacement-time graphs can go below the horizontal axis whereas distance-time graphs can not

    • Distance can not be negative whereas displacement can be

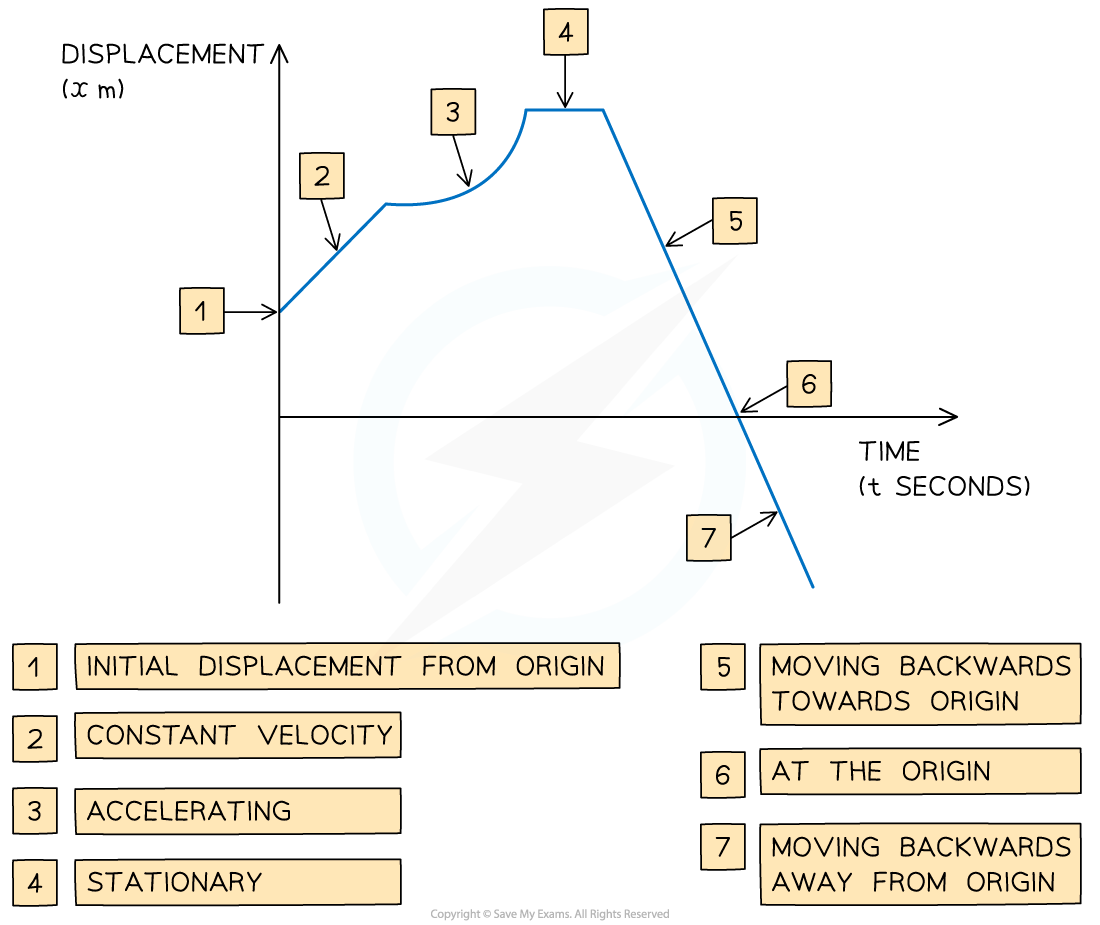
What are the key features of a displacement-time graph?

  • The gradient of the graph equals the velocity of the object

    • A positive gradient means the object is travelling forwards

    • A negative gradient means that the object is travelling backwards

    • The steeper the line, the greater the speed

  • A straight line shows that the object is moving at a constant velocity

  • A curved line shows that the object is accelerating or decelerating

  • A horizontal line shows that the object is stationary

  • If the graph touches the x-axis, then the object is at the origin at that time

2-1-1-displacement-time-graphs-diagram-1

How do I find the average speed and the average velocity of a journey?

Average space speed =  fraction numerator Total space distance space travelled over denominator Time space taken end fraction

  • The average speed can not be negative as speed is a scalar quantity and can only take a positive value

Average space velocity space equals space fraction numerator Displacement space from space starting space point over denominator Time space taken end fraction

  • The average velocity is a vector quantity and can be positive, zero or negative

Worked Example

An athlete is training by jogging in a straight line.

The displacement-time graph below shows the displacement of the athlete from her starting point throughout her motion.

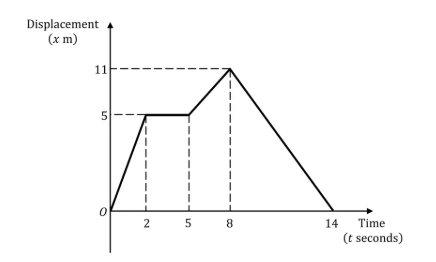
Graph showing displacement versus time. Displacement: 0-11m. Time: 0-14s. Segments: 0-2s rising, 2-5s flat, 5-8s rising, 8-14s falling.

(a)   Calculate the velocity of the athlete during the first 2 seconds.

2-1-1-displacement-time-graphs-example-solution-1-a

(b)    Describe the motion of the athlete between the times of 2 seconds and 5 seconds.

2-1-1-displacement-time-graphs-example-solution-1-b

(c)   Calculate the velocity of the athlete at 10 seconds.

2-1-1-displacement-time-graphs-example-solution-c

(d)   Find the total distanced travelled by the athlete during the 14 seconds.

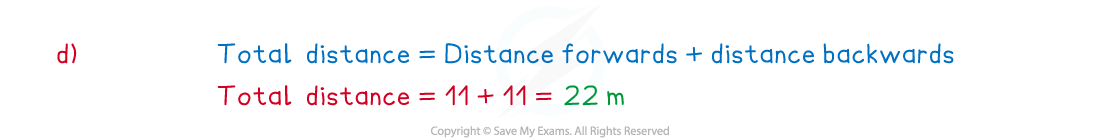
2-1-1-displacement-time-graphs-example-solution-d

Examiner Tips and Tricks

  • Be careful to spot if you are working with a displacement-time graph or a velocity-time graph.

  • Be careful to spot if you are working with a displacement-time graph or a distance-time graph

  • Check where the graph starts from on the y-axis, the object does not have to start at 0. For example, if the graph starts at 100, the scenario could be a student on a walk starting 100 m from their house.

  • Distance is a scalar so it can not be negative whereas displacement from a starting point can be.

  • Think about the units when calculating, make sure they are consistent.

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Modelling AssumptionsNext:Velocity-Time Graphs
Dan Finlay

Author: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Displacement-Time Graphs