Square Roots of a Complex Number using Exponential Form (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Square roots of a complex number using exponential form
Previously we looked at how to find the square roots of a complex number in Cartesian form (a+bi). We can also find square roots using polar () and exponential form (
).
How do I find a square root of a complex number in exponential form?
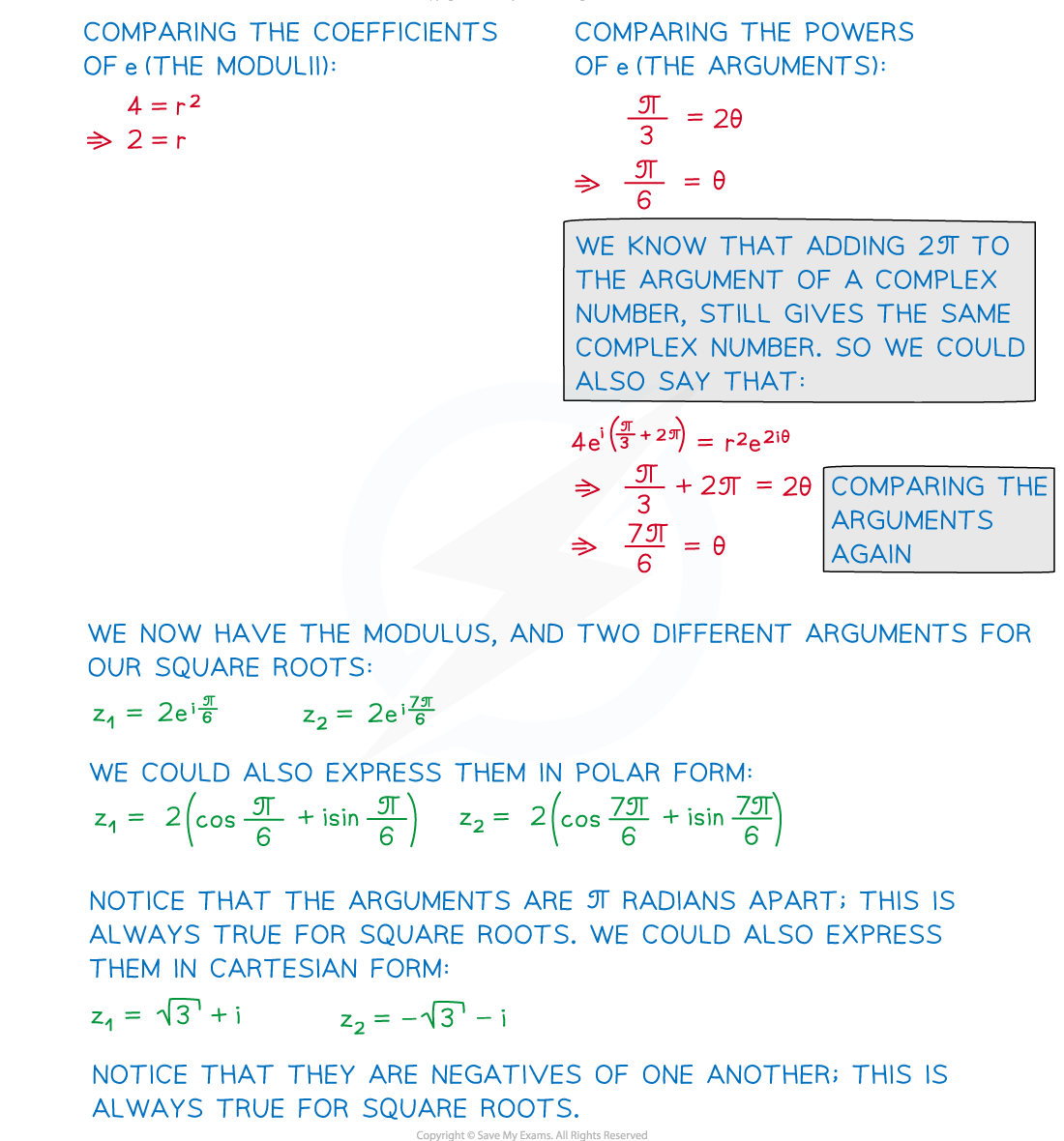
Let
be a square root of
Applying rules of indices:
Comparing the coefficients of e (moduli) and powers of e (arguments) we can state:
A square root of
is
Square root the modulus
Halve the argument
How do I find the second square root?
The second square root is the first one multiplied by -1
and
We can write the second one in polar or exponential form too
Adding 2π to the argument of a complex number still gives the same complex number
So we could also say that
Therefore
is another possibility
So the two square roots of (
) are:
You should notice that the two square roots are π radians apart from each other
This is always true when finding square roots
And if you were to write them in cartesian form they would be negatives of one another
E.g. a+bi and -a-bi
This is also always true when finding square roots
This approach can be extended to find higher order roots (e.g. cube roots) by knowing that the nth roots will be
radians apart from each other, however this is beyond the specification of this course
Examiner Tips and Tricks
The square roots will be negatives of each other when written in cartesian form, and the two square roots will be π radians apart when written in polar form. These two facts can help you find the roots quicker and/or check your answers.
If your calculator is able to work with complex numbers, you should also square the square-roots you found to check that you get the original number.
Worked Example

Examiner Tips and Tricks
The square roots will be negatives of each other when written in cartesian form, and the two square roots will be π radians apart when written in polar form. These two facts can help you find the roots quicker and/or check your answers.
If your calculator is able to work with complex numbers, you should also square the square-roots you found to check that you get the original number.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?