Revision NotesExam QuestionsPast Papers
GCSEMathsEdexcelFoundationRevision NotesAlgebraReal-Life GraphsRates of Change of Graphs

Rates of Change of Graphs (Edexcel GCSE Maths)

Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Edexcel Maths: FoundationEdexcel Maths: Higher

Rates of Change of Graphs

What is a rate-of-change graph?

  • A rate-of-change graph usually shows how a variable changes with time

  • The following are examples of rates-of-change graphs:

    • Speed against time

      • Speed is the rate of change of distance as time increases

    • Acceleration against time

      • Acceleration is the rate of change of velocity as time increases

    • The depth of water against time (e.g. in a container as it is filled with water)

Diff Basics Notes fig1, downloadable IGCSE & GCSE Maths revision notes

Can rates-of-change graphs not be against time?

  • More generally, rate-of-change graphs can show any two different variables plotted against each other, not just time

    • E.g. the volume of air inside an inflating balloon plotted against the balloon's radius

      • This shows the rate of change of volume as radius increases

    • E.g. the number of ice-creams sold plotted against the weather temperature

      • This shows the rate of change of number of ice-creams as temperature increases

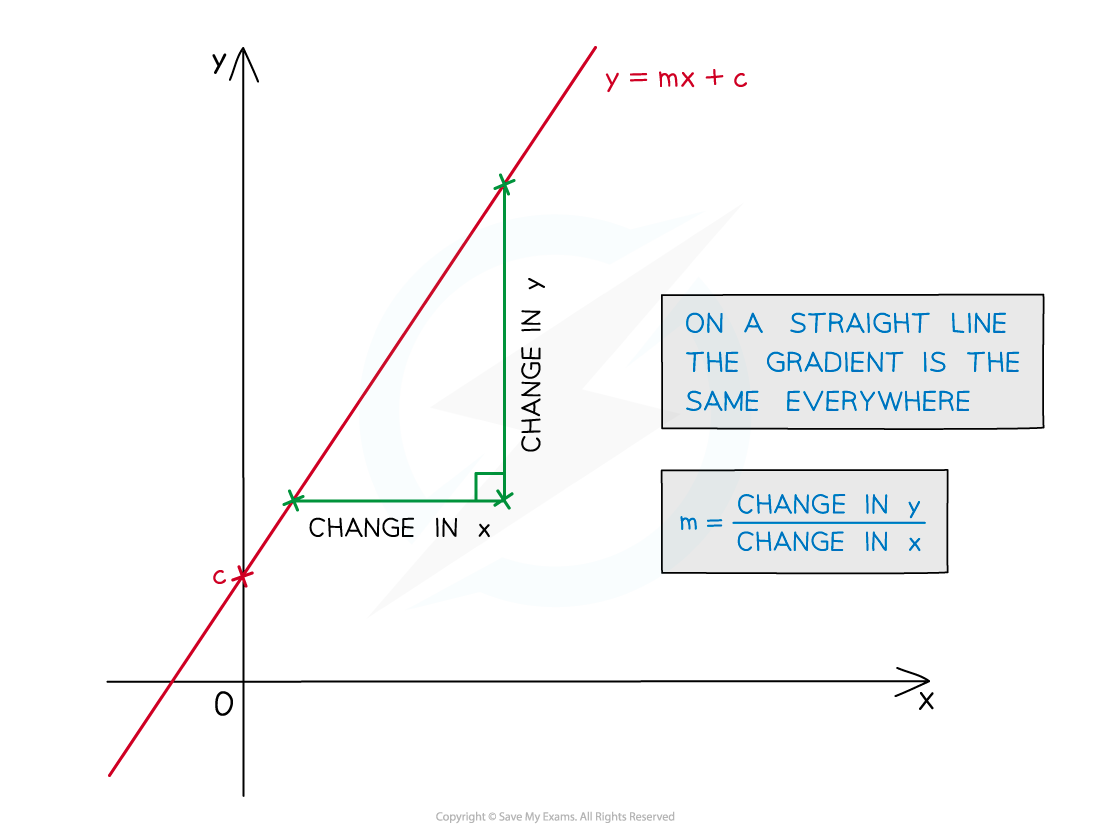
How can I use gradients to find rates of change?

  • The gradient of the graph of y against x represents:

    • the amount of change in y for every 1 unit of increase in the x-direction

      • This is the amount of y per unit of x

    • This is called the rate of change of y against x

  • The units of gradients are the units of the y-axis, divided by the units of the x-axis

    • E.g. If the graph shows volume in cm3 on the y-axis and time in seconds on the x-axis, the rate of change is measured in cm3/s (or cm3s-1)

  • If the graph is a straight line the rate of change is constant

    • If the graph is horizontal, the rate of change is zero

      • y is not changing as x changes

Diff Basics Notes fig3, downloadable IGCSE & GCSE Maths revision notes

How can I use tangents to find rates of change?

  • If the graph is a curve, you can draw a tangent at a point on the graph and find its gradient

    • This will be an estimate of the rate of change of y against x

  • The rate of change is greater when the graph is steeper

    • In the below image

      • tangents drawn at points A and B show the graph is steeper at B

      • therefore the rate of change at B is greater

A graph showing tangents drawn at two points, A and B, on a curve. The tangent at point A has a shallow gradient and the tangent at point B has a steeper gradient.

  • On a distance-time graph, a tangent at a point on the curve can be used to estimate the velocity at that particular time

  • On a speed-time graph, a tangent at a point on the curve can be used to estimate the acceleration at that particular time

Examiner Tips and Tricks

  • The units of the gradient can help you understand what is happening in the context of an exam question

    • For example, if the y-axis is in dollars and the x-axis is in hours, the gradient represents the change in dollars per hour

Worked Example

(a) Each of the graphs below show the depth of water, d cm, in different containers that are being filled from a running tap of water.

Match each of the graphs 1, 2, 3, 4 with the containers A, B, C, D.

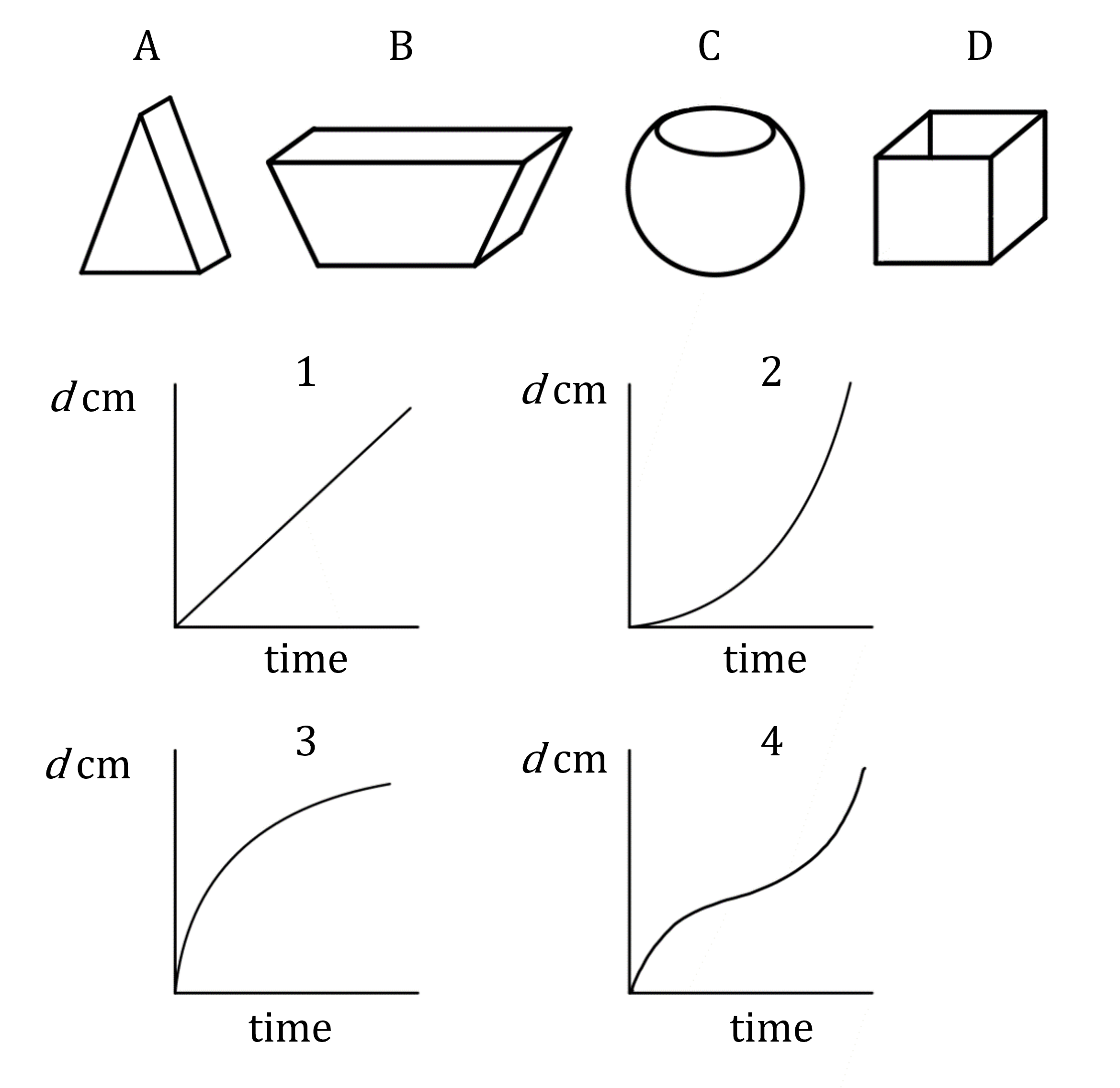
rates-of-change-of-graphs-we-a-containers-and-graphs-2

Considering graph 1: the gradient is constant
This means the rate of change is constant
So the depth increases at the same rate throughout

This matches container D which has vertical sides, so depth increases uniformly

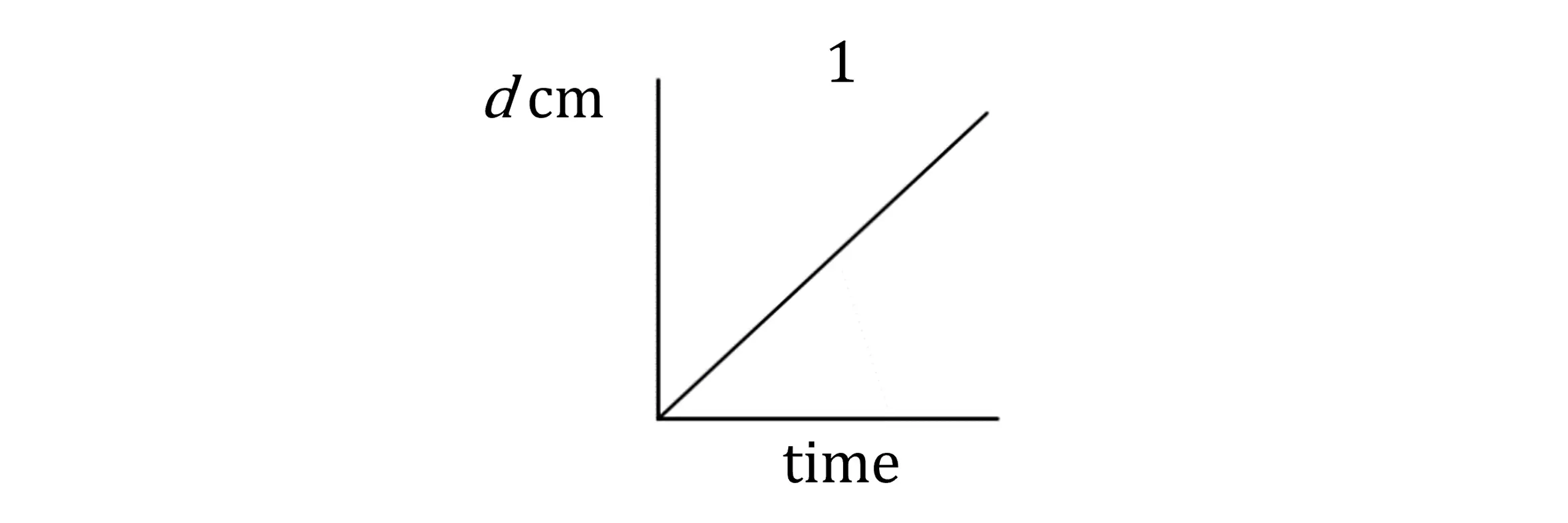
Graph 1 - Linear relationship.

Graph 1 is container D

Considering graph 2: the gradient starts shallow and becomes steeper, meaning that the depth increases faster and faster at the end

This matches container A, which gets narrower towards the top, causing the depth to increase faster at the end

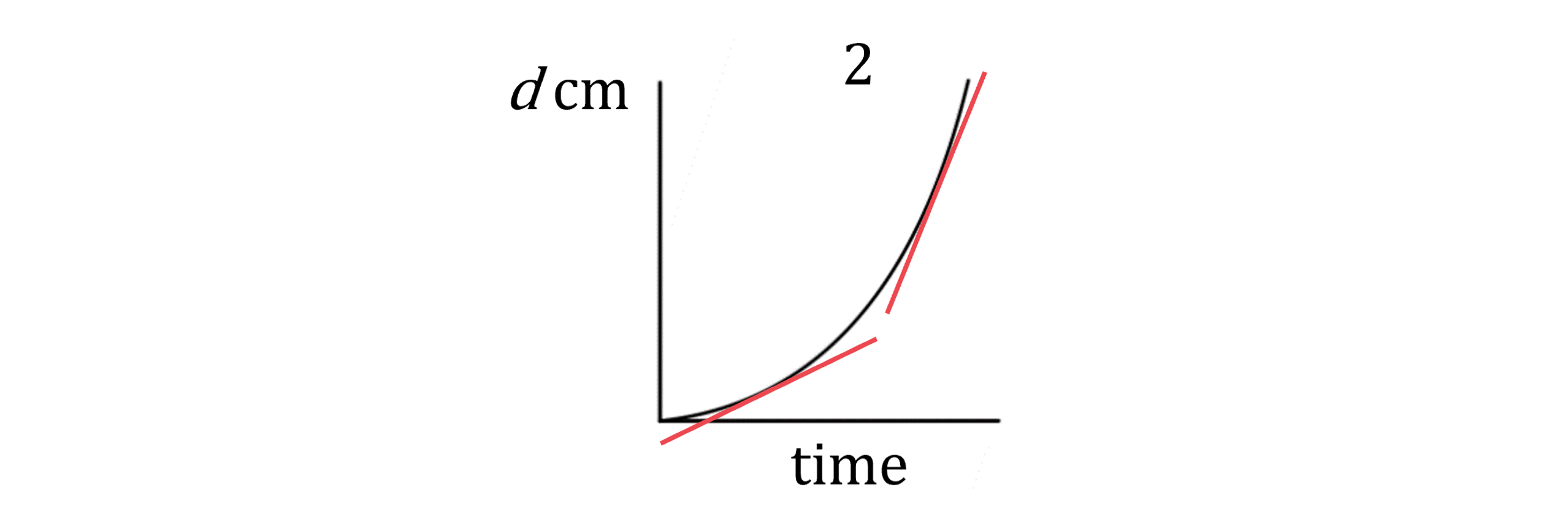
Graph 2. This graph starts with a shallow gradient that gets steeper as x is increased.

Graph 2 is container A

Considering graph 3: the gradient starts steep and becomes shallower, meaning that the depth increases at a slower and slower rate as time increases

This matches container B, which gets wider towards the top, causing the depth to increase more slowly at the end

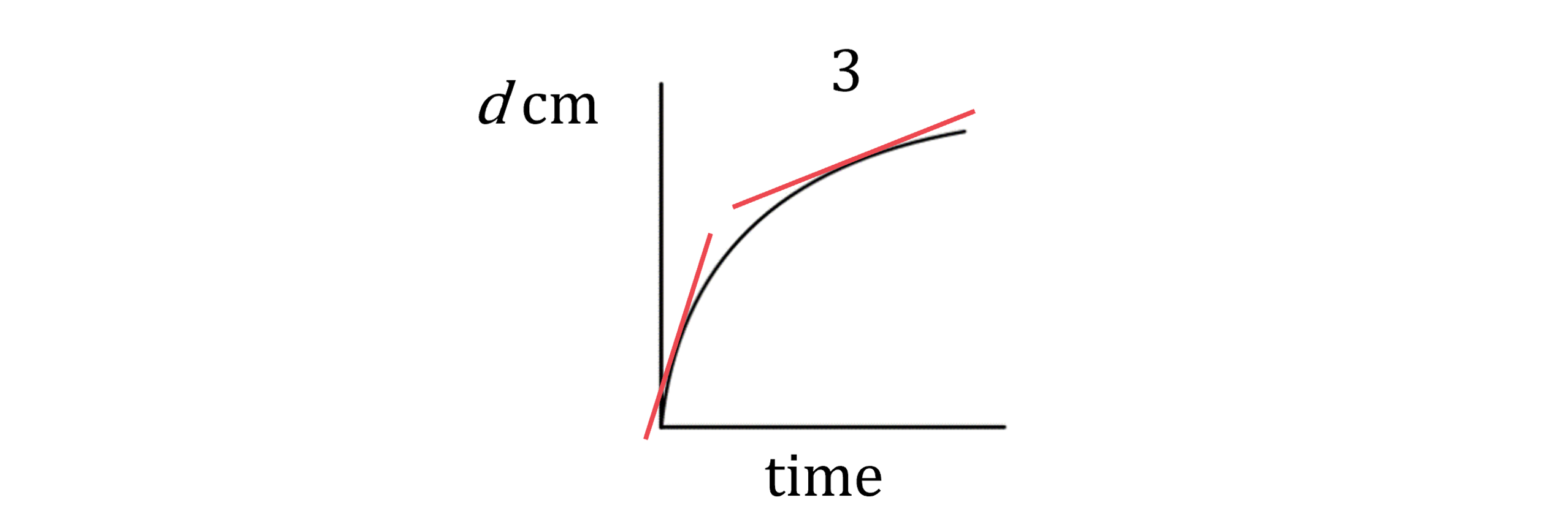
Graph 3: This shows a curve that starts with a steep gradient that gradually gets shallower.

Graph 3 is container B

Considering graph 4: the gradient starts steep, then becomes shallow, then becomes steep again. This means that the depth increases quickly, then slowly, then quickly again

This matches container C, which is narrow at the bottom (fast depth increase), gets wider in the middle (slower depth increase) and narrow again at the top (faster depth increase)

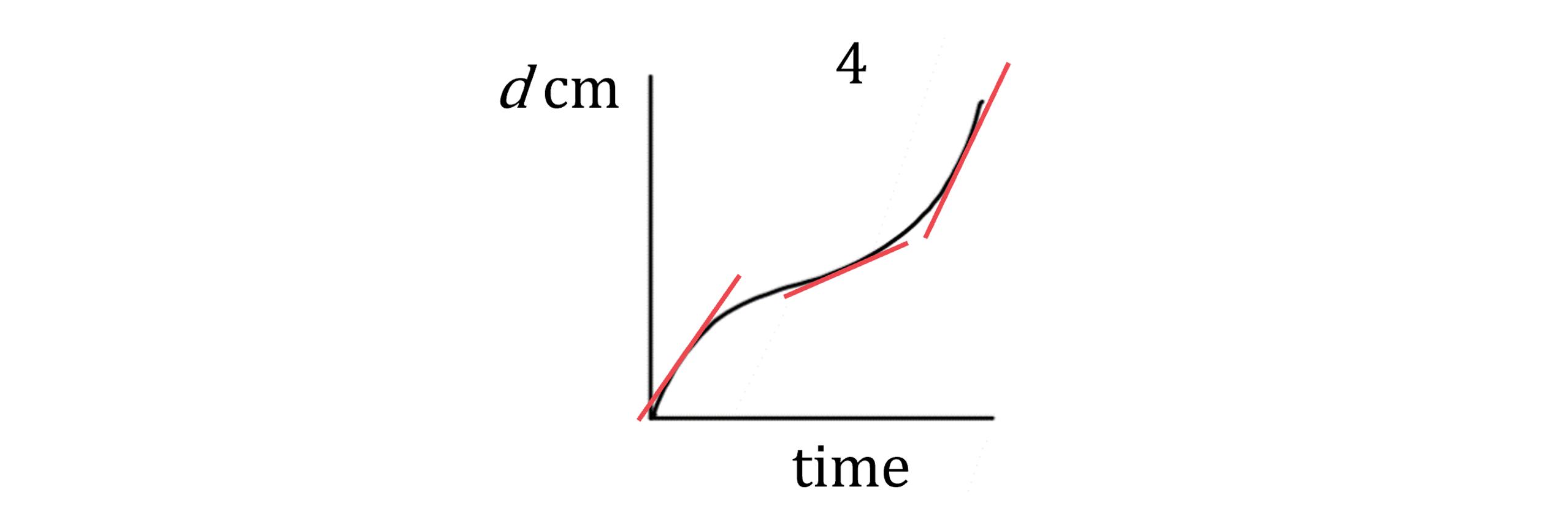
Graph 4: This shows a curve that starts with a steep gradient that gets a bit shallower, but then starts to get steeper again.

Graph 4 is container C

(b) The graph below shows a model of the volume, v litres, of diesel fuel in the tank of George’s truck after it has travelled a distance of d kilometres.

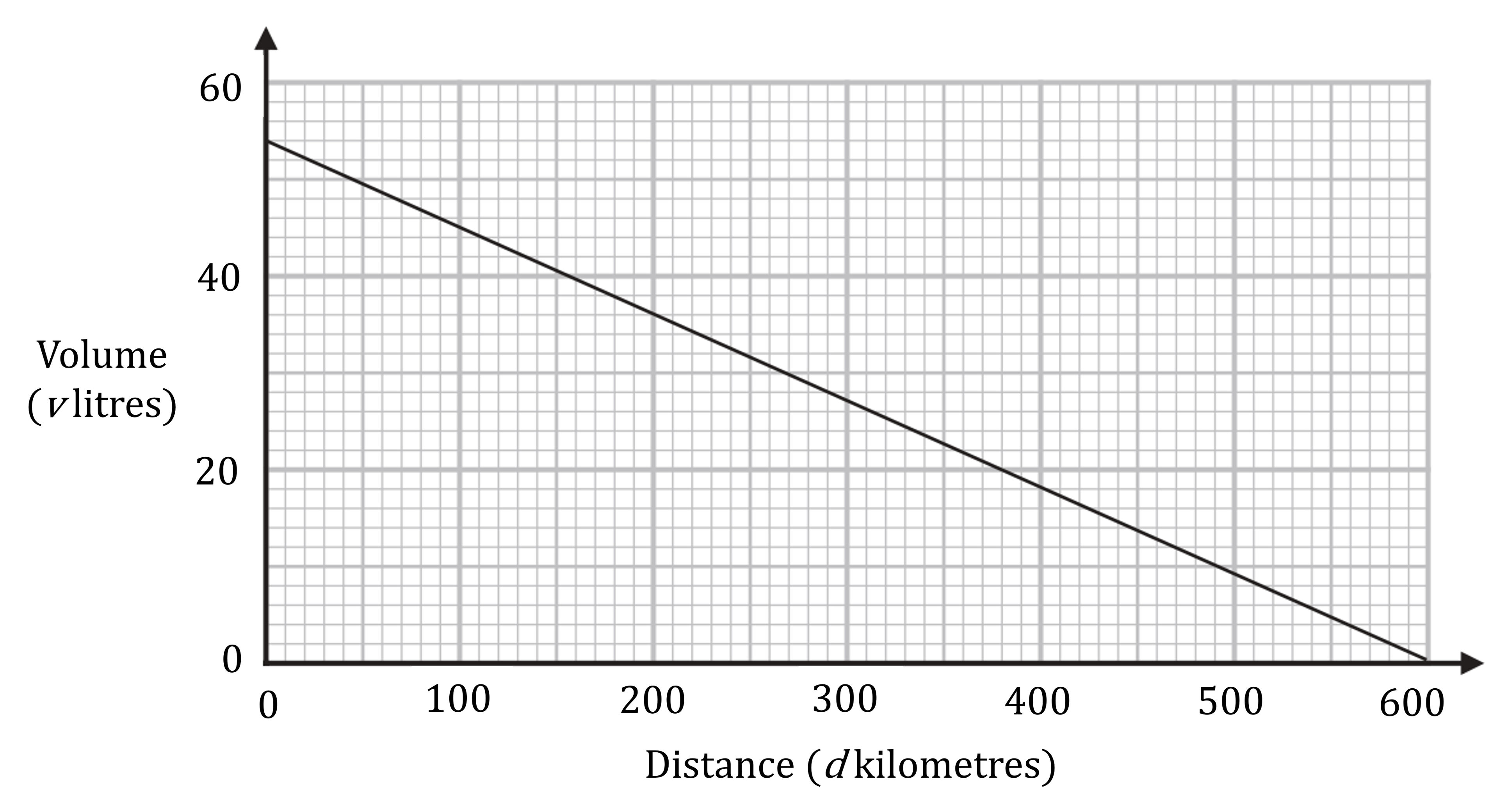
BxxbOqQK_rates-of-change-of-graphs-we-b-graph

(i) Find the gradient of the graph, stating its units clearly.

Gradient space equals fraction numerator change space in space y space over denominator change space in space x end fraction

Gradient space equals space fraction numerator negative 54 space litres over denominator 600 space kilometres end fraction space

-0.09 litres per kilometre

(ii) Interpret what the gradient of this graph represents.

Consider the units of the gradient: litres per kilometre
An increase in 1 kilometres causes a decreases of 0.09 litres in diesel fuel

The gradient represents the amount of diesel fuel used to travel one kilometre
Travelling 1 km uses up 0.09 litres of diesel fuel

(iii) Give one reason why this model may not be realistic.

Fuel may not be consumed at a constant rate
(The rate may vary as the driver accelerates)
(The rate may be different at the beginning when the truck weighs more)

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Conversion GraphsNext:Interpreting Inequalities
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.