GCSEMaths: FoundationEdexcelRevision NotesGeometry & MeasuresBearings, Scale Drawing, Constructions & LociConstructions & Loci

Constructions & Loci (Edexcel GCSE Maths: Foundation)

Revision Note

Test yourself
Jamie W

Author

Jamie W

Last updated

Constructions

What are constructions?

  • A construction is a process where you create particular geometric objects using only a pair of compasses and a straight edge (and a sharp pencil!)
  • There are several types of construction you must be able to carry out:
    • A perpendicular bisector
      • This is a line that cuts another one exactly in half (bisects) but also crosses it at a right angle (perpendicular)
      • It shows a path that is equidistant (equal distance) between the two endpoints of the line
    • A perpendicular from a point to a line
      • This is the shortest line between the point and the line
    • An angle bisector
      • This is a line that cuts an angle exactly in half (bisects)
      • It shows a path that is equidistant (equal distance) between the two lines that form the angle

How do I construct a perpendicular bisector of a line?

  • STEP 1
    Set the distance between the point of the compasses and the pencil to be more than half the length of the line
  • STEP 2
    Place the point of the compasses on one end of the line and sketch an arc above and below the line
  • STEP 3
    Place the point of the compasses on the other end of the line and sketch an arc above and below the line
    • Keep your compasses set to the same distance
    • The arcs should intersect each other both above and below the line
  • STEP 4
    Connect the points where the arcs intersect with a straight line

Constructing a perpendicular bisector

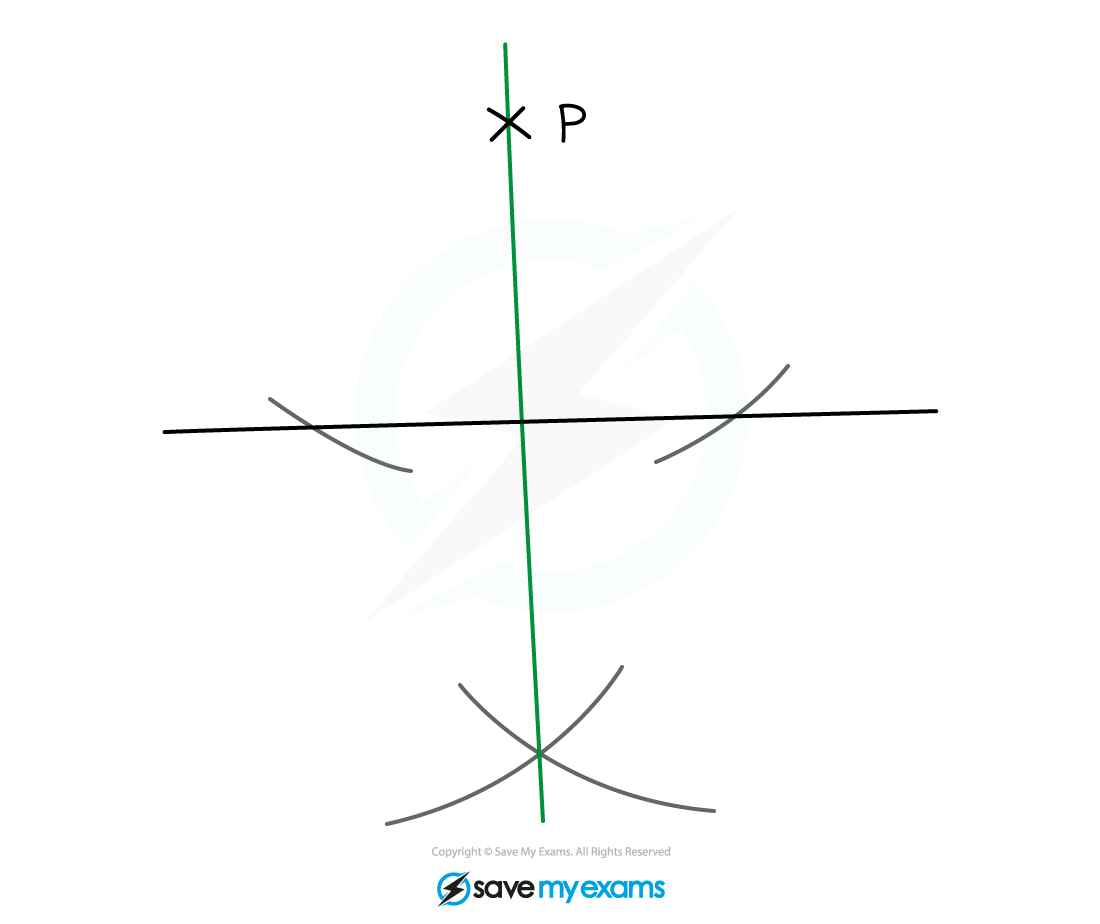
How do I construct a perpendicular from a point to a line?

  • STEP 1
    Set the distance between the point of your compasses and the pencil to be greater than the distance between the point P and the line
  • STEP 2
    Placing the point of the compasses onto the point P, draw an arc that intersects the line in two places
  • STEP 3
    Set the distance between the point of the compasses and the pencil to be more than half the distance between the two points of intersection on the line
  • STEP 4
    Place the point of the compasses on one point of intersection and sketch an arc on the other side of the line to P
  • STEP 5
    Place the point of the compasses on the other point of intersection and sketch an another arc
    • Keep your compasses set to the same distance
    • The arcs should intersect
  • STEP 6
    Connect the point where the arcs intersect to point P with a straight line

Constructing a perpendicular from a point to a line

How do I construct an angle bisector?

  • STEP 1
    Set the distance between the point of your compasses and the pencil to be about half the distance of the smallest line that makes the angle
    • The precise distance is not important
  • STEP 2
    Place the point of the compasses where the lines meet and sketch an arc that intersects both of the lines that form the angle
  • STEP 3
    Place the point of the compasses on one of the points of intersection and sketch an arc
    • Keep your compasses set to the same distance
  • STEP 4
    Place the point of the compasses on the other point of intersection and sketch an arc
    • This should intersect the last arc drawn
    • Keep your compasses set to the same distance
  • STEP 5
    Join the point of the angle to the point of intersection with a straight line

Constructing an angle bisector

Examiner Tip

  • Make sure you have all the equipment you need; pen, pencil, ruler, compasses, protractor, calculator
  • An eraser and a pencil sharpener can be helpful on these questions as they are all about accuracy
    • But do not erase your construction lines
  • Make sure your compasses aren’t loose and wobbly, and make sure you can see and read the markings on your ruler and protractor

Loci

What are loci?

  • A locus (loci is plural) is a line, shape, or path that is determined by following a restriction
    • e.g. always being 2 m away from a point would form a circular locus
  • You may be asked to construct a locus, although the exam question won’t always use these words as questions are often based on real-world situations
  • You may be expected to use some of the constructions mentioned above
  • You may need to use a ruler, and a protractor or a pair of compasses

What are the common types of loci?

  • A fixed distance from a point
    • This locus will be a circle around the point
      • Use a pair of compasses
  • A fixed distance from a line
    • This locus will be a running track shape
      • A pair of parallel lines
      • A semi-circle at each end
  • Equidistant from two points
    • This locus will be the perpendicular bisector of the line segment connecting the two points
  • Equidistant from two lines
    • This locus will be the angle bisector of the angle between the two lines

How do I know which region to shade?

  • To find the region that is (or is not) within a given distance from a point
    • Draw a circle around that point
      • The radius will be the given distance
    • The region inside the circle is closer to the point that the given distance
    • The region outside the circle is further away from the point than the given distance
  • To find the region that is closer to point A than point B
    • Draw a straight line that joins A to B
    • Draw the perpendicular bisector of the line
    • The region that is closer to A is the side of the perpendicular bisector that contains A
  • To find the region that is closer to line AB then line AC
    • Draw the angle bisector at point A
      • This is the point where the two lines meet
    • The region that is closer to the AB is the side of the angle bisector that contains line AB
  • You might have to share the region that satisfies multiple conditions
    • Deal with one condition at a time
    • Put a tick in the region(s) that satisfy that condition
      • Put a cross in the region(s) that do not
    • Once all conditions have been dealt with, shade the region that only contains ticks and no crosses

Worked example

On triangle ABC below, indicate the region that is closer to the side AC than the side BC.

General Triangle ABC, IGCSE & GCSE Maths revision notes

 

This question is asking for the region that is closer to one side of an angle than the other, so an angle bisector is needed 

Open your set of compasses to a distance that is approximately half the length of the sides AB and AC.
This distance is not too important, but keeping it the same length throughout the question is very important

Place the point of the compasses at A and draw arcs across the lines AB and AC. Be very careful not to change the length of the compasses as you draw the arcs

Leaving the compasses open at the same length, put the point at each of the places where the arcs cross the sides AB and AC and draw new arcs which cross over each other in the middle

General Triangle ABC with arcs, IGCSE & GCSE Maths revision notes   

Draw a line from A to the point where the arcs cross over each other (this won't necessarily be directly on the third side of the triangle!)

Shade the region between the angle bisector (the line you have drawn) and the side AC

General Triangle ABC with angle bisected & shaded, IGCSE & GCSE Maths revision notes

Worked example

A house lies between Town A and Town B as shown on the scale diagram below.

Towns and Masts, IGCSE & GCSE Maths revision notes

Two masts, located at the points R and S, provide the area shown on the map with radio signals.
The house will receive its radio signal for the mast located at point R if it is either... 
... closer to Town A than Town B, or...
... outside a region 5 miles from the mast at point S.

Showing your working carefully on the scale diagram below, determine whether the house receives radio signals from the mast at point R or the mast at point S.

Begin by finding the region satisfying the first condition; that the house is closer to Town A than Town B

This is found by constructing the perpendicular bisector of the line segment that joins Town A and Town B
You will need to add this line segment in yourself before starting

Open your compasses to more than half of the distance from Town A to Town B and draw arcs both above and below the line joining Town A to Town B
Do this from both the point at Town A and the point at Town B. The arcs should cross over each other
 

Towns and Masts with arcs, IGCSE & GCSE Maths revision notes

The perpendicular bisector is the line that passes through both of the points where the arcs cross over each other

Towns and Masts with arcs & bisector, IGCSE & GCSE Maths revision notesThe house is on the same side of the perpendicular bisector as Town B is

The house is closer to Town B than Town A.

Now check the second condition; to see if the house is further than 5 miles from the mast at point S.
To find the locus of points exactly 5 miles from point S, first consider the scale given on the scale drawing.

1 cm = 1 mile
5 cm = 5 miles

Open your set of compasses to exactly 5 cm. Measure this carefully using a ruler.

Pair of Compasses and Ruler, IGCSE & GCSE Maths revision notesBeing extra careful not to change the length of your compasses, put the point at S and draw a circle around S with a radius of 5 cm
You may not be able to draw the full circle, but make sure you have the part that is near the point where the house is located

Town and Masts Complete, IGCSE & GCSE Maths revision notes

The house is located outside of this region, so it is more than 5 miles from the mast at the point S  

The house satisfies one of the conditions given to receive its signal from the mast at point R 

The house receives its radio signal from the mast at point R.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Jamie W

    Author: Jamie W

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.