Linear Simultaneous Equations (Cambridge (CIE) IGCSE Additional Maths): Revision Note
Exam code: 606
Did this video help you?
Elimination method
What are simultaneous linear equations?
When there are two unknowns (say x and y) in a problem, we need two equations to be able to find them both: these are called simultaneous equations
you solve two equations to find two unknowns, x and y
for example, 3x + 2y = 11 and 2x - y = 5
the solutions are x = 3 and y = 1
If they just have x and y in them (no x2 or y2 or xy etc) then they are linear simultaneous equations
Solving a pair of simultaneous equations means finding pairs of values that make both equations true at the same time
A linear equation in two unknowns will produce a straight line if you graph it... linear = line
A pair of simultaneous equations will produce lines that will cross each other (if there is a solution!)
How do I use elimination to solve simultaneous linear equations?
"Elimination" completely removes one of the variables, x or y
Begin by multiplying one (or both) of the equations by a constant (or constants)to get the numbers in front of one of the unknowns to match
For example to eliminate the x's from 3x + 2y = 11 and 2x - y = 5
Multiply every term in the first equation by 2 6x + 4y = 22
Multiply every term in the second equation by 3 6x - 3y = 15
If the matching numbers have the same sign, then subtract one equation from the other
If the matching numbers have different signs then add the equations together
Subtract the second result from the first to eliminate the 6x's
4y - (-3y) = 22 - 15
7y = 7
Solve the new equation to find the value of one of the unknowns
Solve to find y
y = 1
Substitute the value into one of the original equations and solve to find the value of the other unknown
Substitute y = 1 back into either original equation
3x + 2(1) = 11
x = 3
Alternatively, to eliminate the y's from 3x + 2y = 11 and 2x - y = 5
Multiply every term in the second equation by 2
4x - 2y = 10
Add this result to the first equation to eliminate the 2y's (as 2y + (-2y) = 0)
The process then continues as above
Check your final solutions satisfy both equations
3(3) + 2(1) = 11 and 2(3) - (1) = 5
How do I solve linear simultaneous equations from worded contexts?


Examiner Tips and Tricks
Don't skip the checking step (it only takes a few seconds) – there are many places to go wrong when solving simultaneous equations!
Mishandling minus signs is probably the single biggest cause of student error in simultaneous equations questions
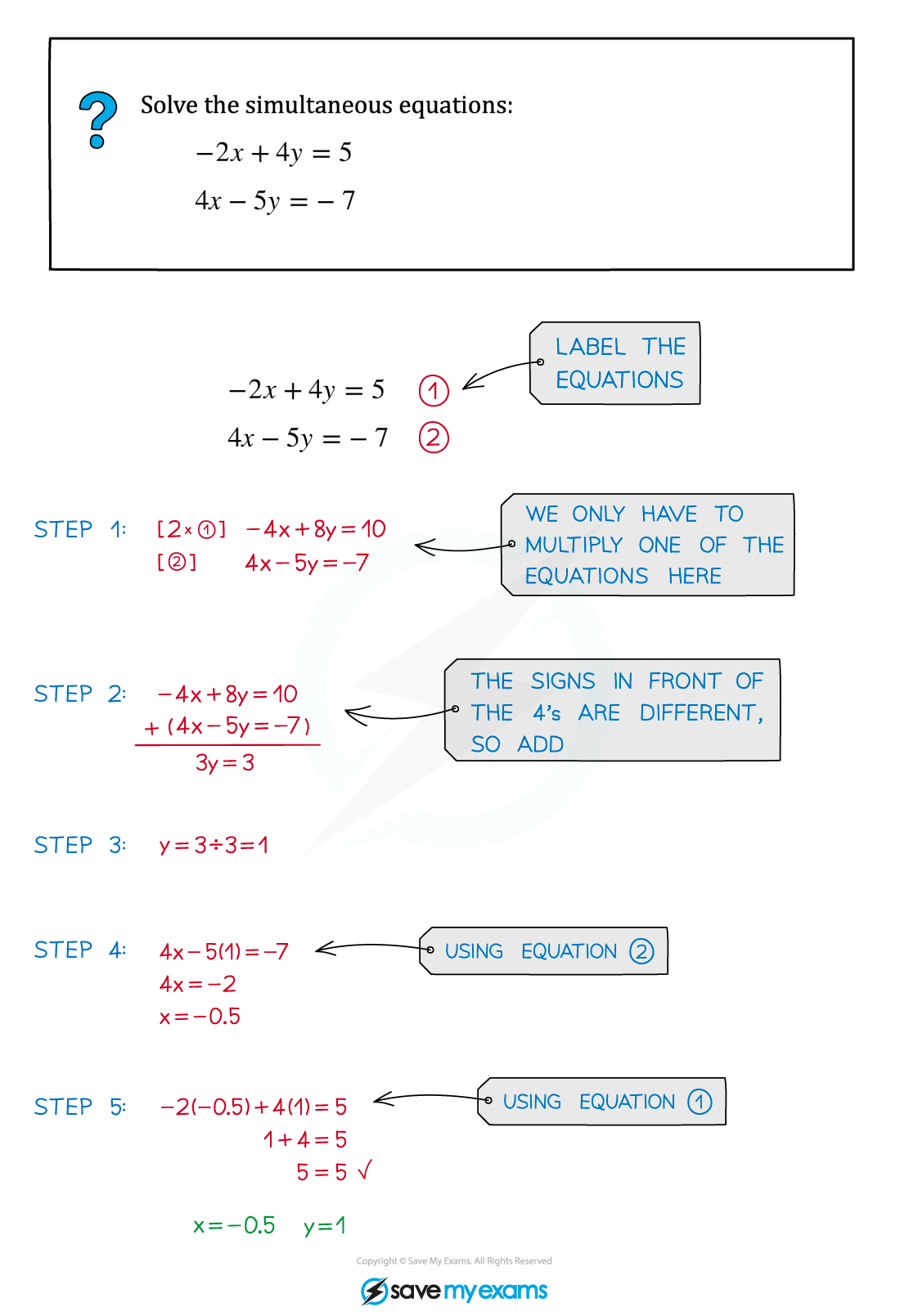
Worked Example
Did this video help you?
Substitution method
How do I use substitution to solve simultaneous linear equations?
"Substitution" means substituting one equation into the other
Rearrange one of the equations to make one of the unknowns the subject
To solve 3x + 2y = 11 and 2x - y = 5 by substitution
Rearrange one of the equation into y = ... (or x = ...)
For example, the second equation becomes y = 2x - 5
Substitute the expression found for x or y into the equation not used to rearrange
Replace all y's with 2x - 5 in brackets
3x + 2(2x - 5) = 11
Solve the new equation to find the value of one of the unknowns
Solve this equation to find x
x = 3
Substitute the value found for x or y into the rearranged equation from to find the value of the other unknown
Substitute x = 3 into y = 2x - 5 to find y
y = 2(3) - 5
y = 1
Check your final solutions satisfy both equations
3(3) + 2(1) = 11 and 2(3) - (1) = 5
How do you use graphs to solve linear simultaneous equations?
Plot both equations on the same set of axes
to do this, you can use a table of values or rearrange into y = mx + c if that helps
Find where the lines intersect (cross over)
The x and y solutions to the simultaneous equations are the x and y coordinates of the point of intersection
e.g. to solve 2x - y = 3 and 3x + y = 4 simultaneously, first plot them both (see graph)
find the point of intersection, (2, 1)
the solution is x = 2 and y = 1

Examiner Tips and Tricks
Although elimination will always work to solve simultaneous linear equations, sometimes substitution can be easier and quicker
Knowing both methods can help you a lot in the exam (plus you will need substitution to solve quadratic simultaneous equations)
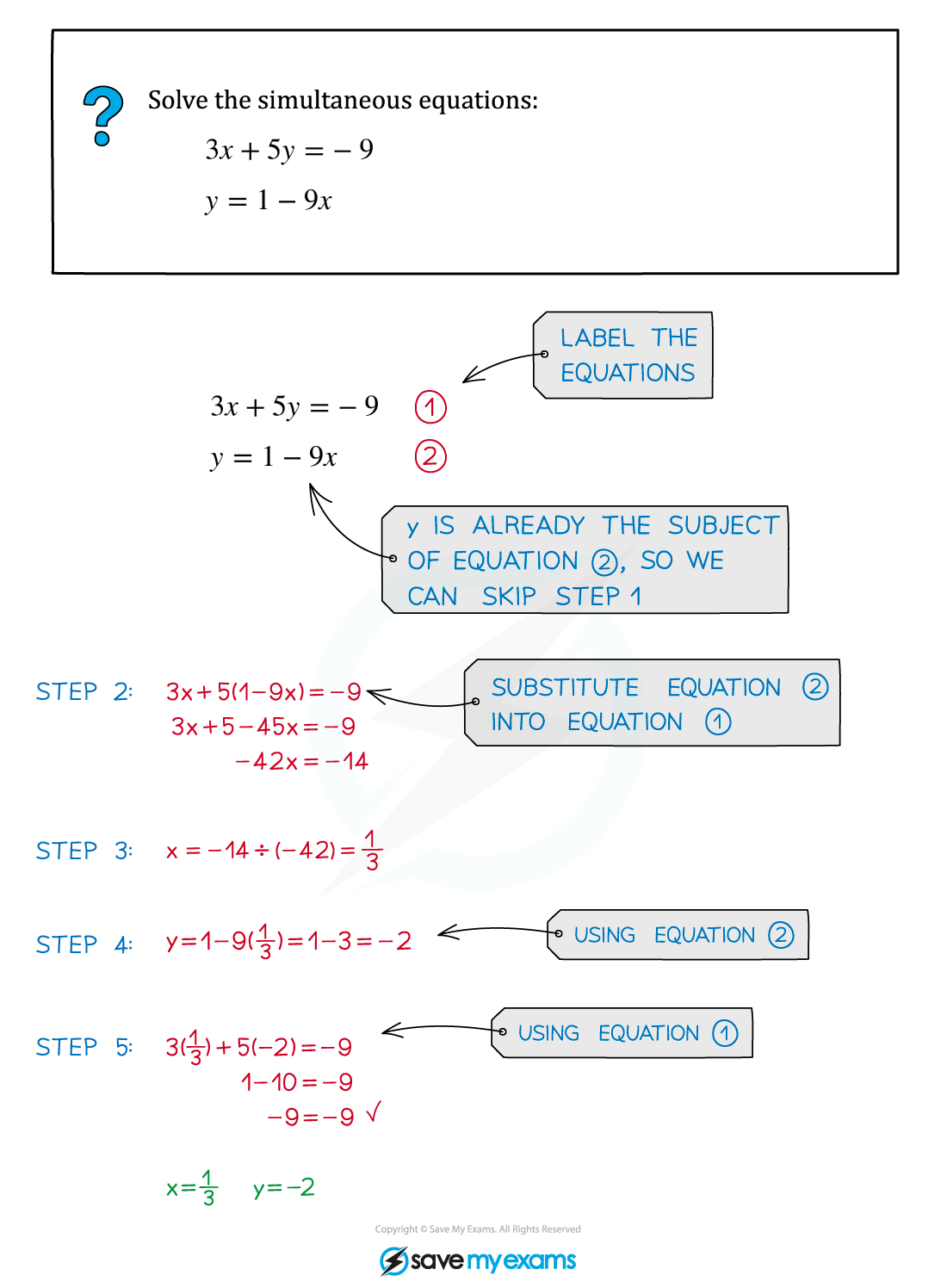
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?