Vectors & Motion (College Board AP® Physics 1: Algebra-Based): Exam Questions

Figure 1

Two identical spheres are released from a device at time from the same height , as shown above. The device is shown in Figure 1.

Sphere A has no initial velocity and falls straight down. Sphere B is given an initial horizontal velocity of magnitude and travels a horizontal distance before it reaches the ground. The spheres reach the ground at the same time , even though Sphere B has more distance to cover before landing. Air resistance is negligible.

The dots in Figure 2 represent Spheres A and B. Draw a free-body diagram showing and labeling the forces (not components) exerted on each sphere at time .

Figure 2

Derive an expression for the total time of flight of each sphere, in terms of and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference book.

On the axes in Figure 3, sketch and label a graph of the horizontal component of the velocity of Sphere A and of Sphere B as a function of time.

Figure 3

Justify whether your answers to part b) and part c) support the finding that the spheres reach the ground at the same time, even though they travel different distances.

Figure 1

A clay ball of mass is launched at an angle above the horizontal with initial speed . At the moment it reaches the highest point in its trajectory and is moving horizontally, it collides with and sticks to a wooden block of mass , as shown in Figure 1. The block is suspended from a light string of length . The block and the clay then swing up to a maximum height above the block’s initial position and make an angle with the vertical.

On the axes provided in Figure 2 sketch and label graphs of the horizontal and vertical components of the velocity of the clay ball as a function of time from the time the ball is launched to the time it strikes the block.

Figure 2

A projectile is fired from level ground with speed  at an angle  to the ground. The projectile is fired from a few centimeters before position , reaches its maximum height at position , and lands on the ground at position .

i) Derive an expression for the maximum height of the projectile in terms of , , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference book.

ii) Determine an expression for the mass of the projectile in terms of maximum gravitational potential energy , , and physical constants as appropriate.

Figure 1

A group of students are given a projectile launcher which consists of a spring with an attached plate, as shown in Figure 1. When the spring is compressed, the plate can be held in place by a pin at any of three positions A, B, or C.

Figure 2

Figure 2 shows a steel sphere placed against the plate, which is held in place by a pin at position C. The sphere is launched upon release of the pin.

The students have access to the projectile launcher and equipment usually found in a school laboratory.

The students perform an experiment where they measure the range of the projectile and its time of flight. The spring constant of the spring is . The following table shows the horizontal range of each sphere and its time of flight . The students create a graph with plotted on the vertical axis.

Table 1

Indicate which measured or calculated quantity could be plotted on the horizontal axis to yield a linear graph whose slope can be used to calculate an experimental value for the mass of the new sphere. You may use the remaining columns in the table above, as needed, to record any quantities (including units) that are not already in the table.

Vertical Axis: ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ Horizontal Axis: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽

i) On the grid in Figure 3, plot the appropriate quantities to determine the mass of the sphere. Clearly scale and label all axes, including units, as appropriate.

Figure 3

ii) Draw a best fit line to the data graphed in part i).

Calculate an experimental value for the mass of the ball bearing using the best-fit line that you drew in Figure 3 in part ii).

Figure 1

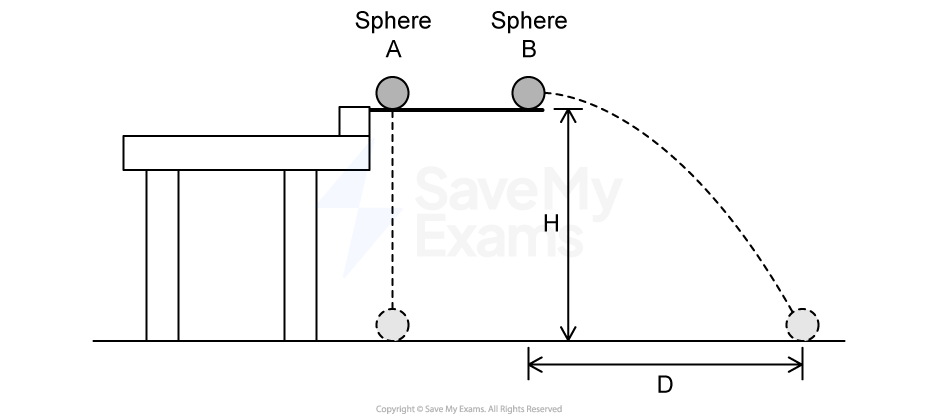
A stunt cyclist builds a ramp that will allow the cyclist to coast down the ramp and jump over several parked cars, as shown above. To test the ramp, the cyclist starts from rest at the top of the ramp, then leaves the ramp, jumps over six cars, and lands on a second ramp.

Figure 1 shows the vertical distance between the top of the first ramp and the launch point, , and the angle of the ramp at the launch point, , as measured from the horizontal. The cyclist travels a horizontal distance of whilst the cyclist and bicycle are in the air. The combined mass of the stunt cyclist and bicycle is .

i) Starting with conservation of energy, derive an expression for the speed of the cyclist as they leave the ramp in terms of and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference booklet.

ii) Starting with a kinematic equation, derive an expression for the distance travelled, in terms of , , and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference booklet.

The ramp is modified so that the cyclist now starts from a height of .

Indicate whether the horizontal distance covered by the stunt cyclist will be less than, equal to, or greater than six cars.

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽

Justify your reasoning.