Study GuidesExam QuestionsPast Papers
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedExam QuestionsUnit 5: Torque & Rotational DynamicsNewton’s First & Second Law in Rotational Form

Newton’s First & Second Law in Rotational Form (College Board AP® Physics 1: Algebra-Based): Exam Questions

27 mins17 questions

Select a download format for Newton’s First & Second Law in Rotational Form

Scroll for more

Select an answer set to view for
Newton’s First & Second Law in Rotational Form

1a
Sme Calculator3 marks
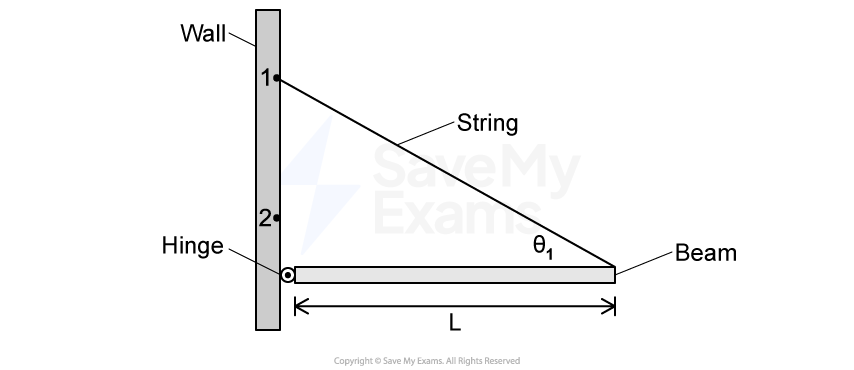
Diagram of a wall with a hinged beam joined horizontally to the wall below point 2. A string is attached to the other end of the beam and is secured to the wall at point 1. The wall, beam and string form a right angled triangle with the string at angle θ1 with respect to the beam. Length L is noted as the length of the beam.

Figure 1

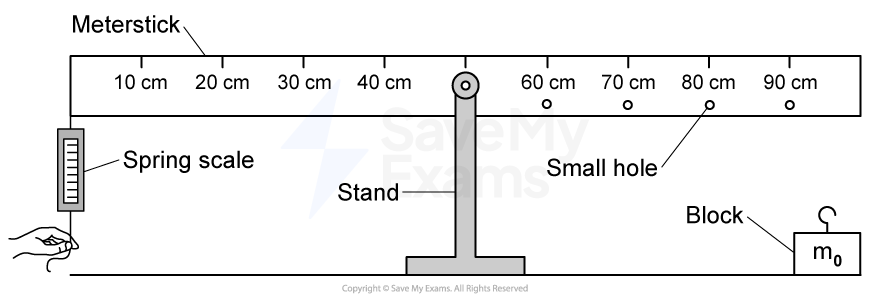
The left end of a uniform beam of mass M and length L is attached to a wall by a hinge, as shown in Figure 1. One end of a string with negligible mass is attached to the right end of the beam. The other end of the string is attached to the wall above the hinge at Point 1. The beam remains horizontal. The hinge exerts a force on the beam of magnitude F subscript H, and the angle between the beam and the string is theta space equals space theta subscript 1.

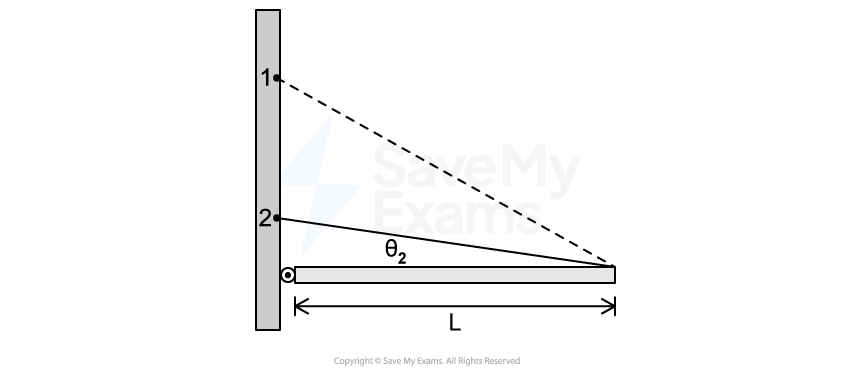
Same hinged beam diagram, but the string is attached to the wall at position 2 which is much lower than position 1. The string forms an angle theta 2 to the beam.

Figure 2

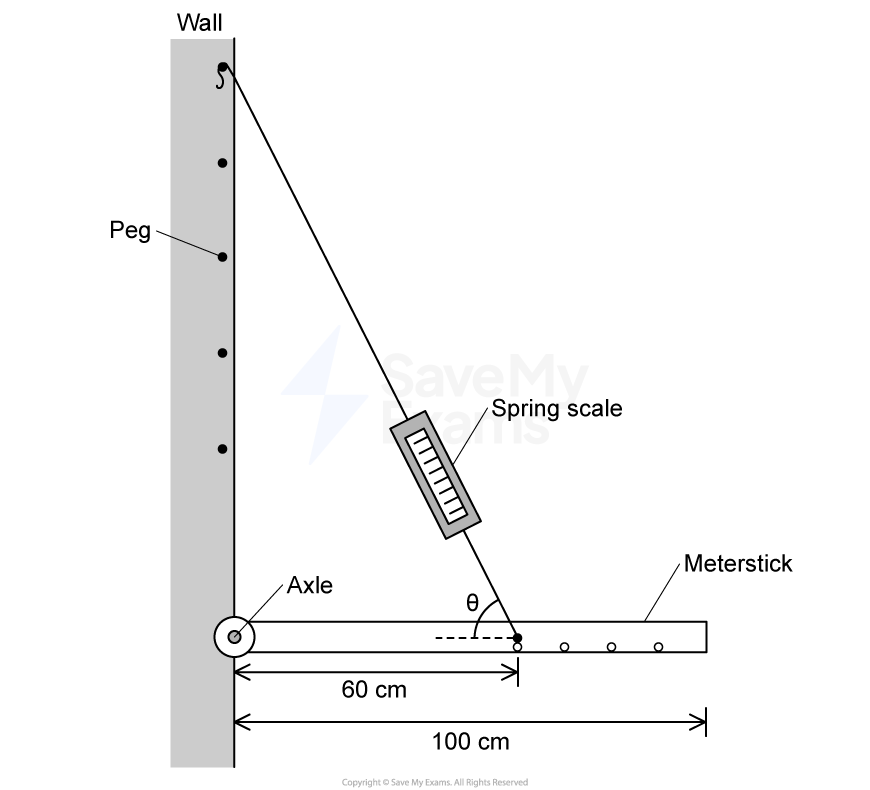
The string is then attached lower on the wall, at Point 2, and the beam remains horizontal, as shown in Figure 2. The angle between the beam and the string is theta space equals space theta subscript 2. The dashed line represents the string shown in Figure 1.

The magnitude of the tension in the string shown in Figure 1 is F subscript T 1 end subscript. The magnitude of the tension in the string shown in Figure 2 is F subscript T 2 end subscript.

Indicate whether F subscript T 2 end subscript is greater than, less than, or equal to F subscript T 1 end subscript.

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ F subscript T 2 end subscript space greater than space F subscript T 1 end subscript‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ F subscript T 2 end subscript space less than space F subscript T 1 end subscript ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ F subscript T 2 end subscript space equals space F subscript T 1 end subscript

Briefly justify your answer, using qualitative reasoning beyond referencing equations.

How did you do?

1b
Sme Calculator3 marks

Starting with Newton’s second law in rotational form, derive an expression for the magnitude of the tension in the string. Express your answer in terms of M, theta, and physical constants, as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference book.

How did you do?

1c
Sme Calculator2 marks

Does the equation you derived in part b) agree with your qualitative reasoning from part a)? Justify why or why not.

How did you do?

Did this page help you?

2a
Sme Calculator2 marks
A pulley of mass M and radius R with a block attached to a string hanging from its radius.

Figure 1

A block of unknown mass is attached to a long, lightweight string that is wrapped several turns around a pulley mounted on a horizontal axis through its center, as shown in Figure 1. The pulley is a uniform solid disk of mass M and radius R. The rotational inertia of the pulley is described by the equation I space equals space 1 half M R squared. The pulley can rotate about its center with negligible friction. The string does not slip on the pulley as the block falls.

When the block is released from rest and as the block travels toward the ground, the magnitude of the tension exerted on the block by the string is F subscript T.

Determine an expression for the magnitude of the angular acceleration alpha subscript D of the disk as the block travels downward. Express your answer in terms of M, R, F subscript T, and physical constants as appropriate.

How did you do?

2b
Sme Calculator2 marks
Diagram comparing two scenarios: a solid disc and a hoop, both with mass M and radius R, under force F_A. The force acts downward in each scenario.

Figure 2

Scenarios 1 and 2 show two different pulleys. In Scenario 1, the pulley is a uniform solid disk of mass M and radius R. In Scenario 2, the pulley is a hoop that has the same mass M and radius R as the disk. Each pulley has a lightweight string wrapped around it several turns and is mounted on a horizontal axle, as shown in Figure 2. Each pulley is free to rotate about its center with negligible friction. In both scenarios, the pulleys begin at rest. Then both strings are pulled with the same constant force F subscript A for the same time interval increment t, causing the pulleys to rotate without the string slipping.

The magnitude of the angular acceleration of the disk is alpha subscript 1. The magnitude of the angular acceleration of the hoop is alpha subscript 2.

Indicate whether alpha subscript 2 is greater than, less than, or equal to alpha subscript 1.

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ alpha subscript 2 space greater than space alpha subscript 1‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ alpha subscript 2 space less than space alpha subscript 1 ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ alpha subscript 2 space equals space alpha subscript 1

Justify your reasoning.

How did you do?

Did this page help you?